Les graphes
Les graphes
Dans un réseau social, il est parfois compliqué de se représenter tous les liens pouvant exister entre les utilisateurs. On utilise en mathématiques des graphes qui permettent de représenter graphiquement les connexions qui existent dans un réseau social.
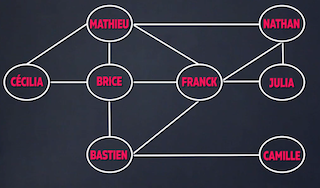
En guise d’exemple, on considère un réseau social ne contenant que 8 abonnés : Mathieu, Nathan, Brice, Julia; Bastien, Camille, Franck et Cécilia.
On représente par un trait les liens d’amitiés entre les abonnés.
On peut alors répondre à divers questions : si tous les utilisateurs ont des amis en commun, comment peut faire un utilisateur pour connecter un ami via d’autres amis, ou si tous les membres du réseau sont connectés.
1) Vocabulaire
Ce type de schéma est appelé un graphe.
Chaque utilisateur représente un sommet du graphe. L’ensemble des sommets est note $V$.
Les connexions entre les utilisateurs sont appelées des arêtes. L’ensemble des arêtes est noté $E$.
Pour déterminer la distance entre deux sommets, on compte le nombre d’arêtes du chemin le plus court les reliant.
Mathieu se situe à une distance de 2 de Bastien.
On parle ici de graphe non orienté car les relations entre les sommets se font dans les deux sens.
Un graphe orienté est donc un graphe où la relation se fait selon un sens précis.
L’écartement est la distance maximale séparant un sommet du reste des sommets du graphe en empruntant le chemin le plus court.
Dans l’exemple du réseau social, l’écartement de Mathieu est de 3 car on doit parcourir au maximum trois arrêtes pour relier deux sommets.
Le centre du graphe est le sommet qui a l’écartement minimal avec les autres sommets du graphe.
Franck est le centre du graphe car il possède un écartement de deux.
Le rayon du graphe est l’écartement entre le centre et le sommet le plus éloigné.
Franck est le centre du graphe, et comme son écartement vaut 2, le rayon du graphe vaut deux.
Le diamètre du graphe représente la distance maximale séparant les deux sommets les plus éloignés.
Le diamètre vaut 3 dans notre exemple, car tous les utilisateurs sont connectés aux autres par un chemin de taille maximale 3.
2) Topologie et architecture des graphes
Il existe trois grandes familles de graphes.
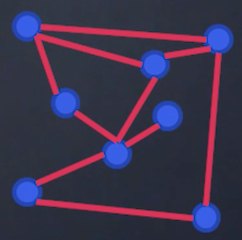
Il existe des graphes quelconques, dont les arrêtes et les sommets sont disposés de manière quelconque.
On peut aussi rencontrer des graphes structurés.
Cette famille est divisée en quatre sous catégories:
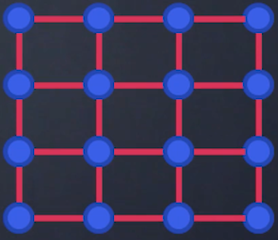
– les graphes homogènes, pour lesquels on observe une régularité dans la construction
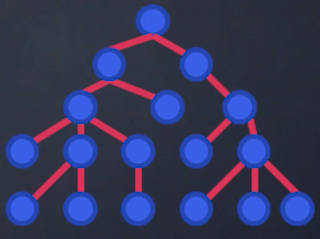
– les graphes hiérarchiques, disposés selon un système pyramidale avec un sommet et des couches successives
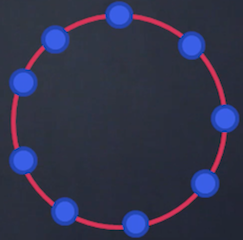
– les graphes cycliques, où l’on observe des cycles à l’intérieur des graphes
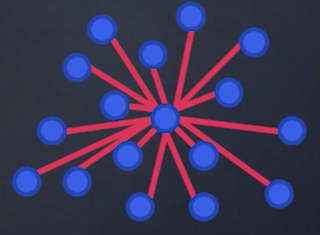
– les graphes centralisés, où l’ensemble des sommets est relié à un seul sommet, appelé le pôle, pouvant servir à représenter un ensemble d’ordinateurs connectés à un même réseau.
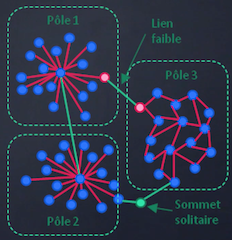
Enfin, il existe des graphes multipolaires, qui présentent des caractéristiques des graphes quelconques et des graphes centralisés.
Chaque pôle est représenté par un graphe centralisé, et des relations existent entre ces différents pôles.
Ce type de graphe peut être utilisé afin de représenter les réseaux sociaux sur internet, où chaque réseau social présente des liens forts entre ces utilisateurs mais qui est connecté à l’extérieur vers d’autres réseaux par des liens faibles.
3) Graphes orientés
On représente les interactions entre les sommets de graphes orientés par des arrêtes sur lesquelles on fait figurer une flèche indiquant l’orientation de l’interaction.
Ces graphes orientés peuvent représenter le cas des réseaux sociaux où l’on peut s’abonner à certaines personnes sans qu’elles ne nous suivent en retour.
Conclusion :
Les graphes sont des outils de représentation graphique, utilisés pour la représentation des réseaux sociaux, le transfert d’information dans un programme, les architectures de réseau ou les systèmes routiers et de communication.