Courant et tension électrique
Courant et tension électrique
I. Définitions à connaître
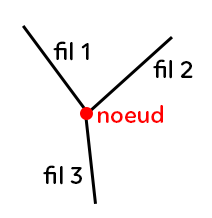
Nœud : endroit dans le circuit où au moins trois fils se rencontrent.
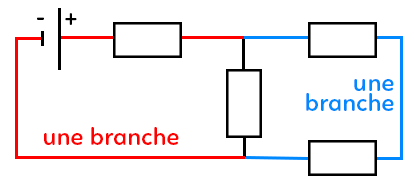
Branche : c’est une portion du circuit entre deux nœuds.
Dipôle : élément du circuit possédant deux pôles : cela peut être une résistance ou bien un pile.
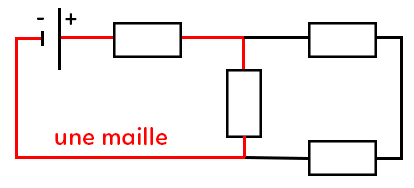
Maille : c’est une succession de branches qui forment une boucle dans le circuit.
II. Le courant électrique
Le courant électrique est proportionnel au débit d’électrons. On peut faire une analogie avec un tuyau d’eau : si le débit est par exemple de 10 L/s, alors si on coupait le tuyau à un endroit, alors il y aurait 10 litres d’eau chaque seconde qui sortirait.
Ainsi, plus le courant électrique est important, plus le débit d’électrons est important. L’intensité du courant électrique est notée $I$ et elle s’exprime en ampère (A). Sur un circuit, on indique le courant avec un chevron sur la branche avec la lettre qui lui correspond à côté.
III. La tension électrique
La tension électrique, ou bien la différence de potentiel, se mesure entre deux points du circuit. On la note souvent U et elle s’exprime en volt (V).
Exemple : $U = 10V.$
Sur un circuit, on trace une flèche pour représenter la tension aux bornes d’un dipôle.
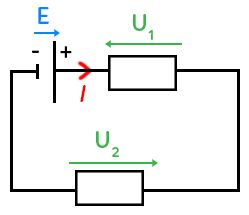
La courant sort de la borne + de la pile (grand côté), il va vers la droite. Les tensions sont notées avec des flèches qui encadrent chaque dipôle. Le sens peut varier selon les dipôles : selon la convention, la flèche pour un générateur (pile) a le même sens que le courant, et pour les autres dipôles elle est en opposition du courant.
Remarque : la tension est nulle le long d’un fil.
Loi des mailles, loi des noeuds
Loi des mailles, loi des noeuds
Ce sont deux lois fondamentales en Physique.
I. Loi des mailles
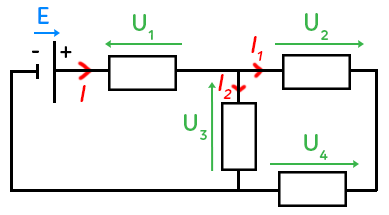
On a un circuit classique avec deux mailles indépendantes (On peut même voir éventuellement une troisième maille.).
On a un générateur (avec la borne « + » et la borne « – »), quatre éléments rectangulaires qui peuvent être des résistors par exemple, des conducteurs ohmiques.
Il faut placer les différentes grandeurs : tension et courant. On choisit d’abord un sens pour la tension. Pour un générateur, la flèche de tension doit être dans le même sens que la flèche du courant. On a indiqué le courant vers la droite ici. La flèche de tension E est dans le même sens que celui-ci.
Les quatre autres composants sont des résistances. C’est-à-dire qu’elles reçoivent de l’énergie. Ce ne sont pas des générateurs mais des récepteurs. Dans ces cas-là, la flèche de tension est opposée à la flèche du courant. On a bien respecté cette règle sur le schéma.
Pour la loi des mailles, il faut commencer par choisir un sens de rotation. On fait la somme des tensions le long de cette maille et cette somme est nulle. La tension est comptée positivement si la tension est dans le même sens que la rotation (par exemple E) et négativement sinon (par exemple $U_1$). Ici, on tourne dans le sens des aiguilles d’une montre, on a : $E-U_1-U_3 = 0.$
C’est la loi des mailles appliquée à la maille de gauche. Si on avait choisi l’autre sens de rotation, est-ce que cela reviendrait au même ? Commençons par $U_3 : U_3+U_1-E = 0.$ Ces deux équations sont les mêmes. Il existe juste un facteur multiplicateur de -1. Le choix du sens d’orientation ne change pas la physique.
II. Loi des nœuds
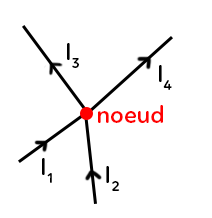
Pour utiliser la loi des nœuds, il faut un nœud : c’est une intersection de branches. Par exemple, ici on a quatre branches qui arrivent au même endroit, en un nœud :
Cette loi dit que la somme des intensités électriques qui rentrent est égale à la somme des intensités des courants électriques qui sortent.
Imaginons des tuyaux qui arrivent. L’eau qui entre dans ces tuyaux et la même qui en sort. Grâce aux flèches, on repère très facilement qu’elles rentrent. En terme de formule : $I_1 + I_2 = I_3 + I_4$ (courants entrants = courants sortants).
La loi d'Ohm
La loi d’Ohm
I. Le résistor
Le résistor est un dipôle représenté par un rectangle. On les appelle parfois par abus de langage des résistances. Ils sont aussi appelés des conducteurs ohmiques. Le résistor est caractérisé par sa résistance en ohm, noté $\Omega.$ Il est traversé par un courant d’intensité $I$ en ampère (A). À ses bornes, le résistor a une tension notée $U$ en volt (V).
II. La loi d’Ohm
$U = R \times I$
La loi d’Ohm va relier le courant qui traverse le dipôle et la tension à ses bornes. C’est donc une loi de linéarité entre $U$ et $I$. Elle sert à la fois pour le résistor, pour les systèmes ohmiques ou pour tout dipôle ohmique.
III. Application
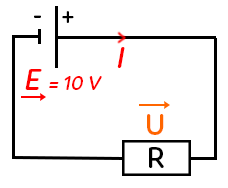
Le circuit est composé d’un générateur et d’un résistor. Le générateur va fonctionner et perdre de l’énergie qui va aller dans le résistor. Le résistor va alors déployer l’énergie sous forme de chaleur par effet Joule.
Cela est souvent inutile sauf dans des appareils comme le grille-pain par exemple, où le résistor rougit en recevant de l’électricité. On rappelle qu’il y a des règles pour représenter les tensions selon si le dipôle est un générateur ou un récepteur.
Une pile est un générateur : la flèche de tension (appelée $E$) est donc dans le même sens que l’intensité du courant (ici vers la droite). Le résistor est un récepteur : sa flèche de tension (appelée $U$) doit donc être dans le sens opposé de celui du courant.
Pour chercher $U$ et $I$, nous allons utiliser la loi des mailles et la loi d’Ohm. Il y a ici une seule maille, dont on choisit le sens (le sens horaire par exemple). La loi des mailles permet d’écrire que : $E – U = 0$ donc $U = E = 10 V$. Pour $I,$ on utilise la loi d’Ohm.
On a donc : $U = R \times I$ d’après la loi d’Ohm soit $I = \dfrac{U}{R} = \dfrac{10}{1000} = 0.01 A$
Attention à ne pas oublier de convertir ainsi que d’indiquer l’unité :
$1 \ kOhm = 1 000\ \Omega$