Droites remarquables dans le triangle
Droites remarquables dans le triangle
1) Hauteur
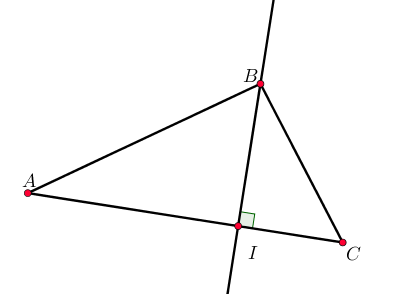
Dans un triangle, la droite perpendiculaire à $[AC]$ passant par $B$ est la hauteur issue de $B$.
Le point $I$ est le pied de la hauteur.
L’intersection des trois hauteur est appelée l’orthocentre du triangle.
2) Médiane
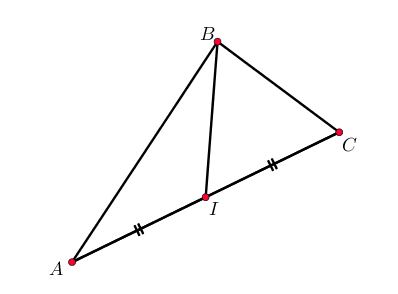
La médiane issue de $B$ est la droite passant par $B$ et par le milieu du côté opposé.
L’intersection des trois médianes s’appelle le centre de gravité $G$.
3) Médiatrice
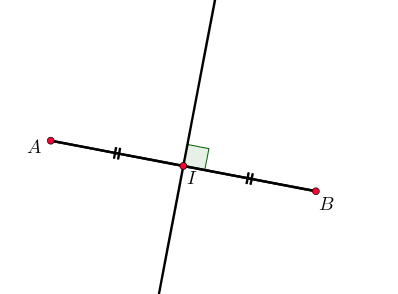
La médiatrice d’un segment est la droite perpendiculaire à ce segment passant par son milieu.
Tout point de la médiatrice est équidistant de $A$ et $B$.
Dans un triangle, le point de concours des médiatrices est le centre du cercle circonscrit.
4) Bissectrice
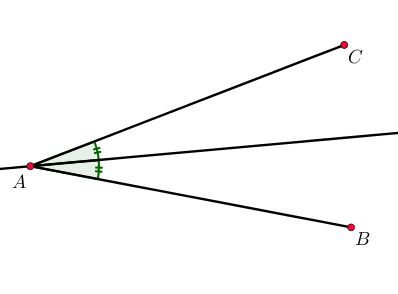
La bissectrice d’un angle est la droite partageant l’angle en deux angles de même mesure.
Dans un triangle, le point d’intersection des trois bissectrices est le centre du cercle inscrit au triangle, tangent intérieurement au côté du triangle.
Théorème de Thalès
Théorème de Thalès
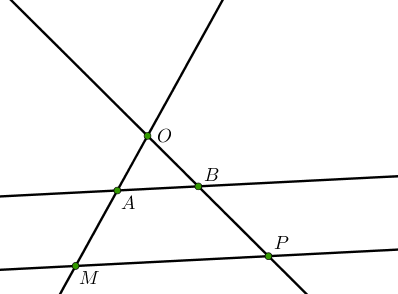
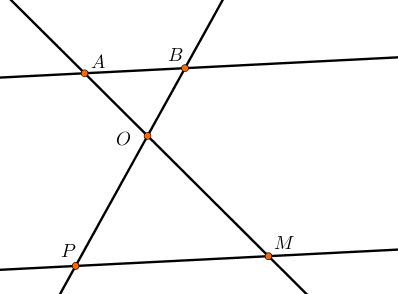
Il existe deux situations où l’on peut appliquer le théorème de Thalès qui sont représentées par le schémas ci-dessous.
Deux droites doivent donc être sécantes et sont coupées par deux droites parallèles.
Théorème
Si $O, A, M$ alignés
$O, B, P$ alignés
$(AB)\ // \ (MP)$
Alors $\dfrac{OA}{OM} = \dfrac{OB}{OP} = \dfrac{AB}{MP}$.
Le point $O$ est appelé le point charnière.
Ce théorème permet d’obtenir des quotients de longueurs, permettant ainsi de trouver des d’autres longueurs.
Exemple :
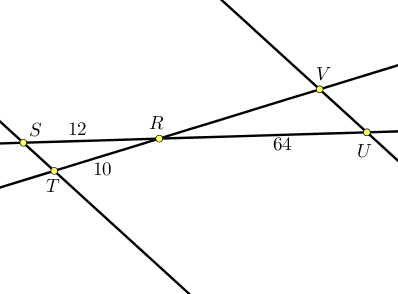
Les points $R, S, U$ sont alignés ainsi que les points $T, R, V$.
Les droites $(ST)$ et $(VU)$ sont parallèles. Donnons une valeur approchée de $RV$ à $10^{-2}$.
D’après le théorème de Thalès, $\dfrac{RU}{RS} = \dfrac{RV}{RT} = \dfrac{VU}{ST}$.
$\dfrac{64}{12} = \dfrac{RV}{10}$
$12 \times RV = 10 \times 64$
$RV = \dfrac{640}{12} \approx 53,33$
NB : à la toute fin de la vidéo, il y a une erreur de calcul, 640/12=53,3 et non 48 🙂 !!
Réciproque du théorème de Thalès
Réciproque du théorème de Thalès
Théorème :
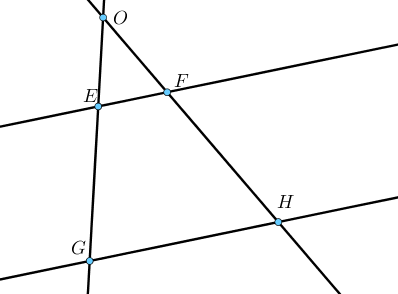
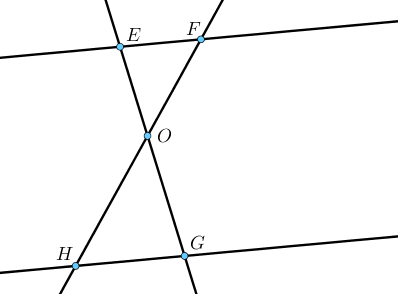
Si $O, E, G$ d’une part et $O, F, H$ d’autre part sont alignés dans le même ordre
et si $\dfrac{OE}{OG} = \dfrac{OF}{OH}$
Alors les droites $(EF)$ et $(GH)$ sont parallèles.
Exemple :
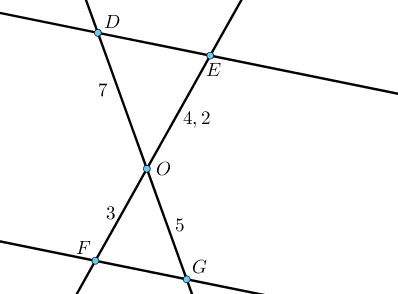
Démontrer que les droites $(DE)$ et $(FG)$ sont parallèles.
On commence donc par calculer de manière distincte $\dfrac{OG}{OD}$ et $\dfrac{OF}{OE}$.
Ainsi $\dfrac{OG}{OD} = \dfrac{5}{7}$.
De même, $\dfrac{OF}{OE} = \dfrac{3}{4,2} = \dfrac{30}{42} = \dfrac{5}{7}$.
Il ne faut pas donner les résultats sous forme approchée car il ne sera plus possible de comparer les deux fractions : il faut donc écrire le résultat sous la forme d’une fraction irréductible.
Donc, $\dfrac{OG}{OD} = \dfrac{OF}{OE}$.
$O, D, G$ d’une part et $O, E, F$ d’autre part sont alignés dans le même ordre.
Alors d’après la réciproque du théorème de Thalès, les droites $(DE)$ et $(FG)$ sont parallèles.