Axe de symétrie et sommet d'une parabole
Déterminer l’axe de symétrie et le sommet d’une parabole d’équation $y =ax^2 + bx + c$
I) Exemples
On commence par traiter deux exemples différents afin de mieux comprendre le cas général.
Exemple 1 :
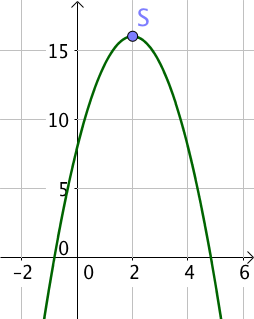
On définit une parabole d’équation $y = -2x^2 + 8x + 8$.
Pour savoir si la parabole est tournée vers le haut ou vers le bas, on regarde le signe de $a$.
Ici, $a = -2 < 0$, la parabole est donc tournée vers le bas. Le sommet de la parabole correspond donc à un maximum.
L’axe de symétrie ($\Delta$) de la parabole est parallèle à l’axe des ordonnées et passe par le sommet. En connaissant les coordonnées du sommet, on pourra en déduire l’équation de l’axe qui sera $x = x_S$, avec $x_S$ l’abscisse du sommet.
On cherche donc les coordonnées du sommet $S$.
On commence par factoriser le polynôme par le coefficient $a$ :
$-2x^2 + 8x + 8 = -2(x^2 – 4x – 4)$.
On cherche à partir des termes $x^2 – 4x$ à faire apparaitre un carré.
Or, en se rappelant les identités remarquables, on sait que $(x – d)^2 = x^2 – 2dx + d^2$, ou encore que $(x – d)^2 – d^2 = x^2 – 2dx$, pour tout réel $d$.
On cherche donc $d$ tel $x^2 – 2dx = x^2 – 4x$ ou encore $-2dx = -4x$ pour tout $x$, et on trouve alors que $d = 2$.
Finalement, on utilise le fait que $(x – d)^2 – d^2 = x^2 – 2dx$ et avec $d = 2$ on trouve $(x – 2)^2 – 2^2 = x^2 – 4x$.
Ainsi, $-2x^2 + 8x + 8 = -2(x^2 – 4x – 4) = -2\big((x-2)^2 – 4 – 4 \big) = -2\big((x-2)^2 – 8 \big)$.
En redéveloppant $-2$ on trouve $-2x^2 + 8x + 8 = -2(x – 2)^2 + 16$. On vient de trouver la forme canonique du polynôme.
On cherche le maximum de la parabole, on cherche donc à maximiser l’équation $-2(x – 2)^2 + 16$.
Or, on se rend compte que le terme $-2(x – 2)^2$ est négatif. On cherche donc $x$ pour lequel cette quantité est la plus grande (donc nulle).
En effet, si cette quantité n’est pas nulle, l’équation sera la différence entre 16 et un nombre positif, donc plus petite que 16.
16 est donc le maximum de la parabole, et cette valeur est atteinte lorsque $-2(x – 2)^2$ est nul, c’est à dire lorsque $x = 2$.
L’abscisse du sommet est donc $2$ et l’ordonnée est la valeur du maximum, c’est à dire $16$.
L’axe de symétrie est donc la droite d’équations $x = 2$.
Exemple 2:
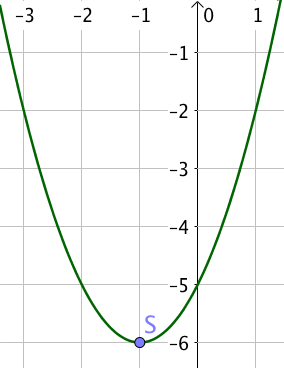
On définit à présent une nouvelle parabole d’équation $y = x^2 +2x – 5$.
Ici, $a = 1 > 0$, donc la parabole est tournée vers le haut. La parabole admet donc un minimum.
L’axe de symétrie est la droite passant par le sommet et parallèle à l’axe des ordonnées.
On cherche donc les coordonnées du sommet $S$.
On réécrit donc l’équation de la parabole pour trouver le $x$ qui la minimise.
Comme le coefficient $a$ vaut $1$, il n’est pas nécessaire de factoriser par $a$.
On cherche alors à faire apparaitre une identité remarquable en cherchant un réel $d$ tel que $(x + d)^2 = x^2 + 2x + d^2 $. Or $(x + d)^2 = x^2 + 2dx + d^2$. On cherche donc $d$ tel que $2dx = 2x$ c’est à dire $d = 1$.
Ainsi, on a l’égalité suivante : $x^2 + 2x = (x + 1)^2 – 1$.
On réécrit alors l’équation de la parabole en faisant apparaitre l’identité remarquable précédente.
$x^2 + 2x – 5 = (x + 1)^2 – 1 – 5 = (x + 1)^2 – 6$.
Comme on cherche le minimum de la parabole, on cherche à minimiser la quantité précédente.
Or, $(x + 1)^2 \geq 0$ par définition, donc $(x + 1)^2 – 6 \geq 0 – 6 = -6$.
En outre, on remarque que si $(x + 1)^2$ est nul, la valeur du polynôme est minimale et vaut $-6$.
Cette valeur est atteinte pour $(x + 1)^2 = 0$ c’est à dire $x + 1 = 0$ ou encore $x = -1$.
Donc le minimum de la parabole est $-6$ et est atteint en $x = -1$.
Finalement, l’axe de symétrie de la parabole a pour équation $x = -1$.
II) Cas général
On cherche à déterminer la forme canonique de la fonction du second degré qui permet de lire directement les coordonnées du sommet et d’en déduire l’axe de symétrie de la parabole.
Soient $a, b$ et $c$ trois réels, ($a \neq 0$),
Soit $x$ un réel,
$\begin{aligned} ax^2 + bx + c &=& a \left ( x^2 + \dfrac{b}{a}x + \dfrac{c}{a} \right ) \end{aligned}$.
On cherche à faire apparaitre une identité remarquable.
$ax^2 + bx + c = a \left ( x^2 + 2 \times \dfrac{b}{2a}x + \left( \dfrac{b}{2a} \right )^2 – \left( \dfrac{b}{2a} \right )^2 + \dfrac{c}{a} \right )$
$ax^2 + bx + c = a \left ( \left( x + \dfrac{b}{2a} \right )^2 – \dfrac{b^2}{4a^2} + \dfrac{c\times 4a}{a \times 4a} \right )$
$ax^2 + bx + c = a \left ( \left( x + \dfrac{b}{2a} \right )^2 – \left ( \dfrac{b^2}{4a^2} – \dfrac{4ac}{4a^2} \right) \right )$
$ax^2 + bx + c = a \left ( \left( x + \dfrac{b}{2a} \right )^2 – \dfrac{b^2 – 4ac}{4a^2} \right )$
On développe alors le $a$ en facteur : $ax^2 + bx + c = a \left( x + \dfrac{b}{2a} \right )^2 – \dfrac{b^2 – 4ac}{4a}$.
Le numérateur du terme $\dfrac{b^2 – 4ac}{4a}$ est appelé le discriminant que l’on note $\Delta = b^2 – 4ac$.
Pour trouver le minimum ou le maximum de la parabole, le terme $a \left( x + \dfrac{b}{2a} \right )^2$ doit être nul, c’est à dire $x = – \dfrac{b}{2a}$.
Finalement, le sommet a pour coordonnés $\left ( \dfrac{-b}{2a}; f \left ( \dfrac{-b}{2a} \right ) \right )$ et son axe de symétrie a pour équation $x = \dfrac{-b}{2a}$.
On pourra remarquer qu’en remplaçant $x$ par $\dfrac{-b}{2a}$ dans l’expression du polynôme on trouve $f \left ( \dfrac{-b}{2a} \right ) = 0 – \dfrac{b^2 – 4ac}{4a}$ donc les coordonnées du sommet sont $\left ( \dfrac{-b}{2a};- \dfrac{b^2 – 4ac}{4a}\right )$.
Enfin, on peut vérifier avec cette propriété les résultats trouvés dans la première partie.
Si $y = 2x^2 + 8x + 8$, alors $a = -2$ et $ b = 8$, donc le minimum a pour abscisse $x = \dfrac{-b}{2a} = \dfrac{-8}{2 \times( -2) } = 2$.
De même si $y = x^2 + 2x -5$, alors $a = 1$ et $ b = 2$, donc le minimum a pour abscisse $x = \dfrac{-b}{2a} = \dfrac{-2}{2 \times 1 } = -1$.


