Signe du trinôme
Signe du trinôme
On s’intéresse au signe du trinôme $f(x) = ax^2 + bx + c$, avec $a \neq 0$.
Le discriminant du trinôme est $\Delta = b^2 – 4ac$.
Si la fonction est positive, elle est au dessus de l’axe des abscisses. Si elle est négative, elle est en dessous. La position de la courbe permet donc de connaître le signe de la fonction.
1) Cas $\Delta < 0$ :
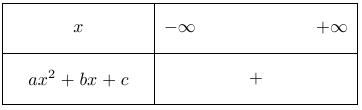
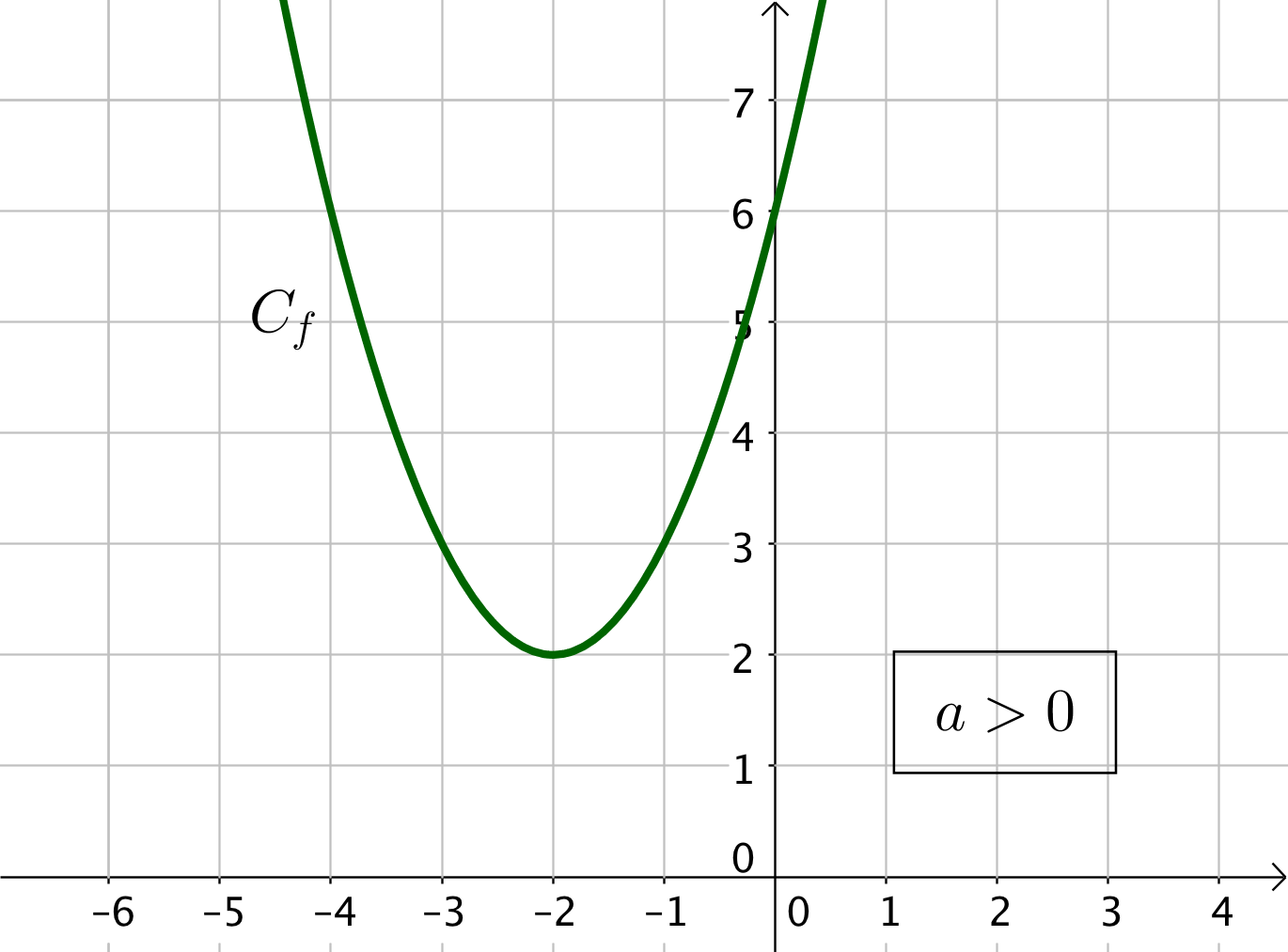
Soit $a>0$ et dans ce cas, la fonction est toujours positive. On indique donc un signe $+$ dans le tableau de signe de la fonction.
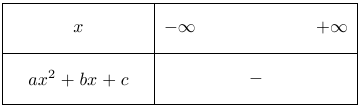
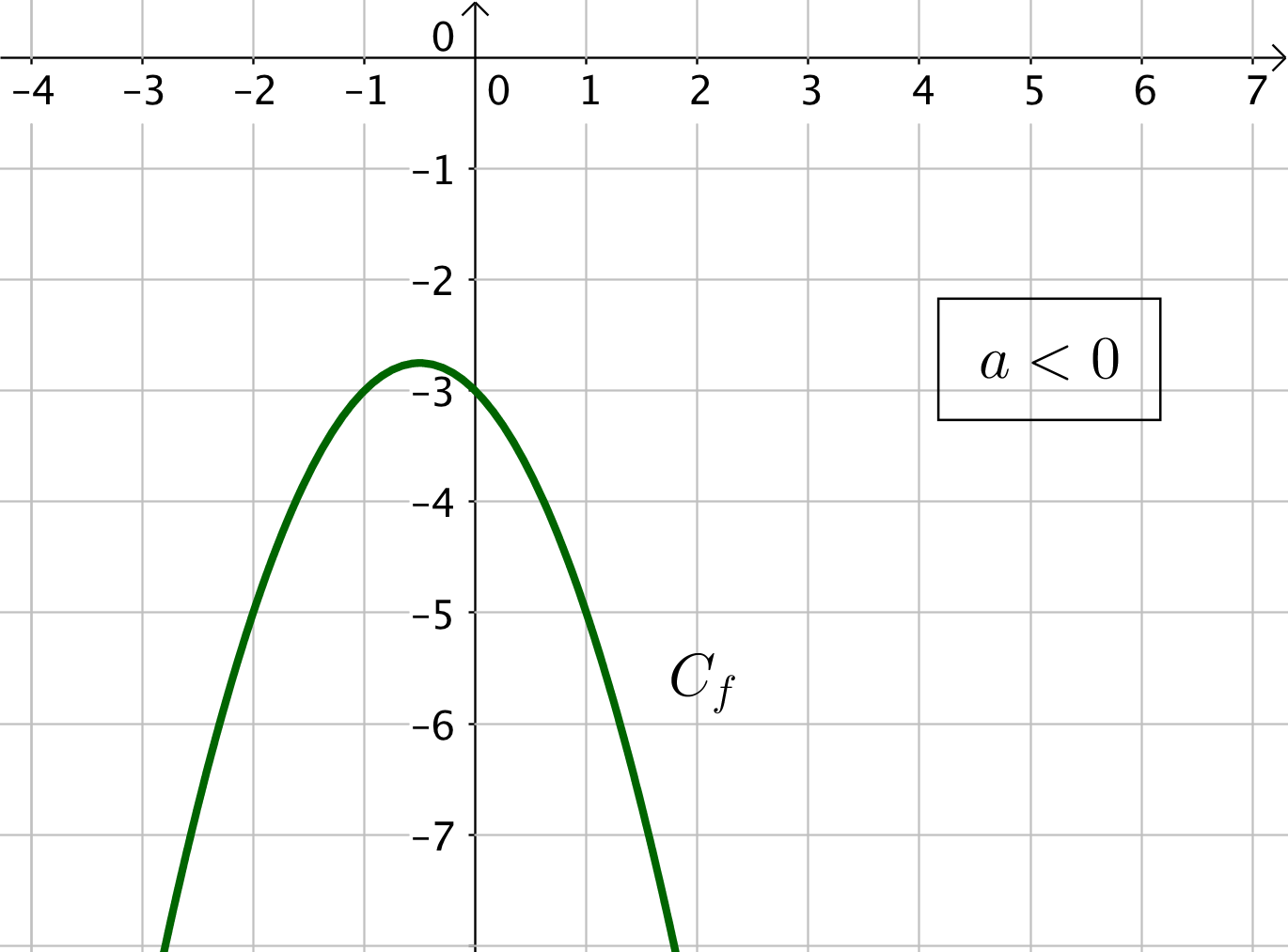
Soit $a < 0$ et la fonction est toujours négative. On indique alors un signe $-$ dans le tableau de signe de la fonction.
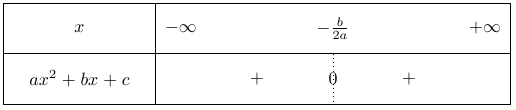
2) Cas où $\Delta = 0$
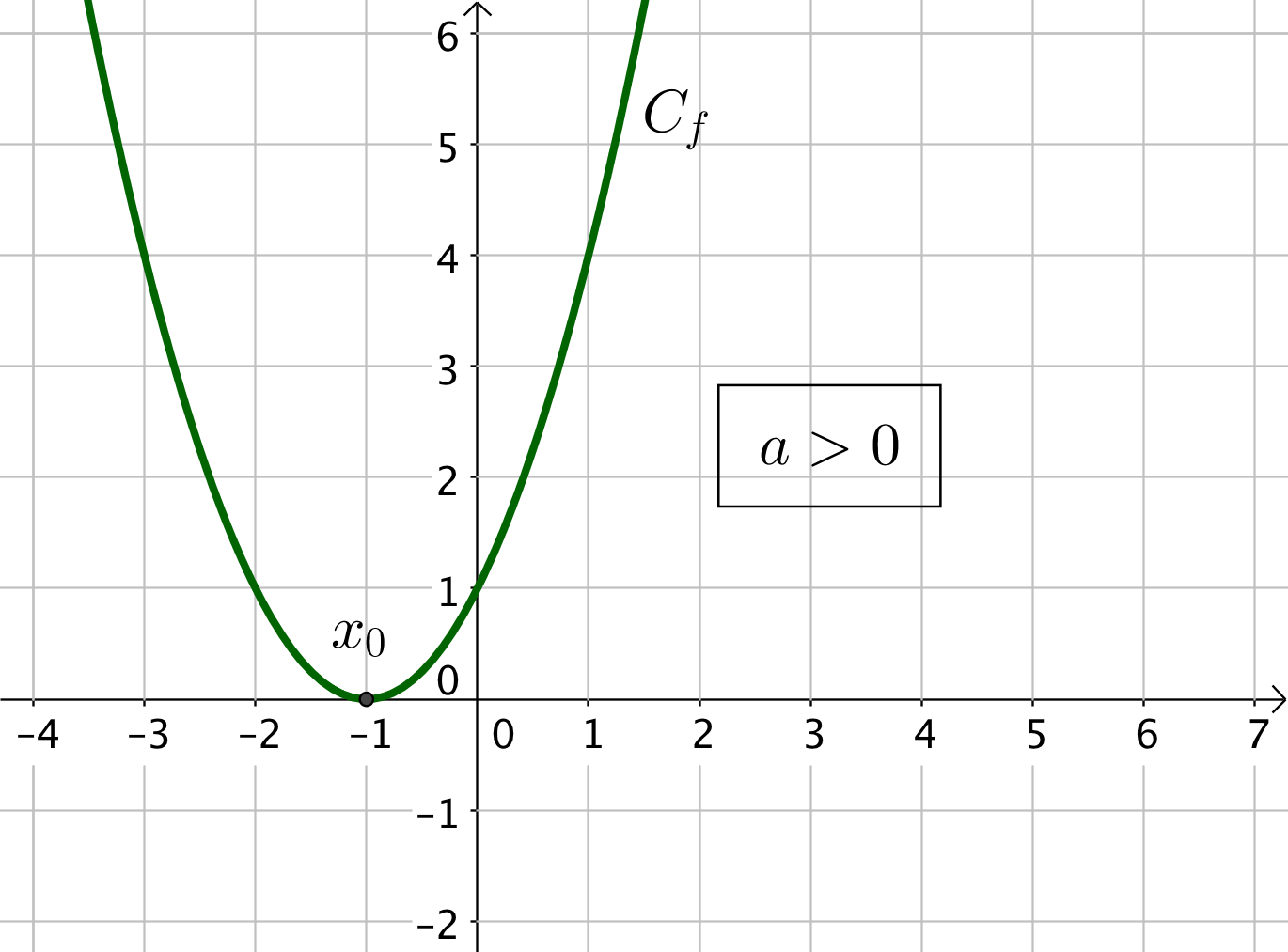
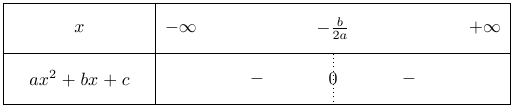
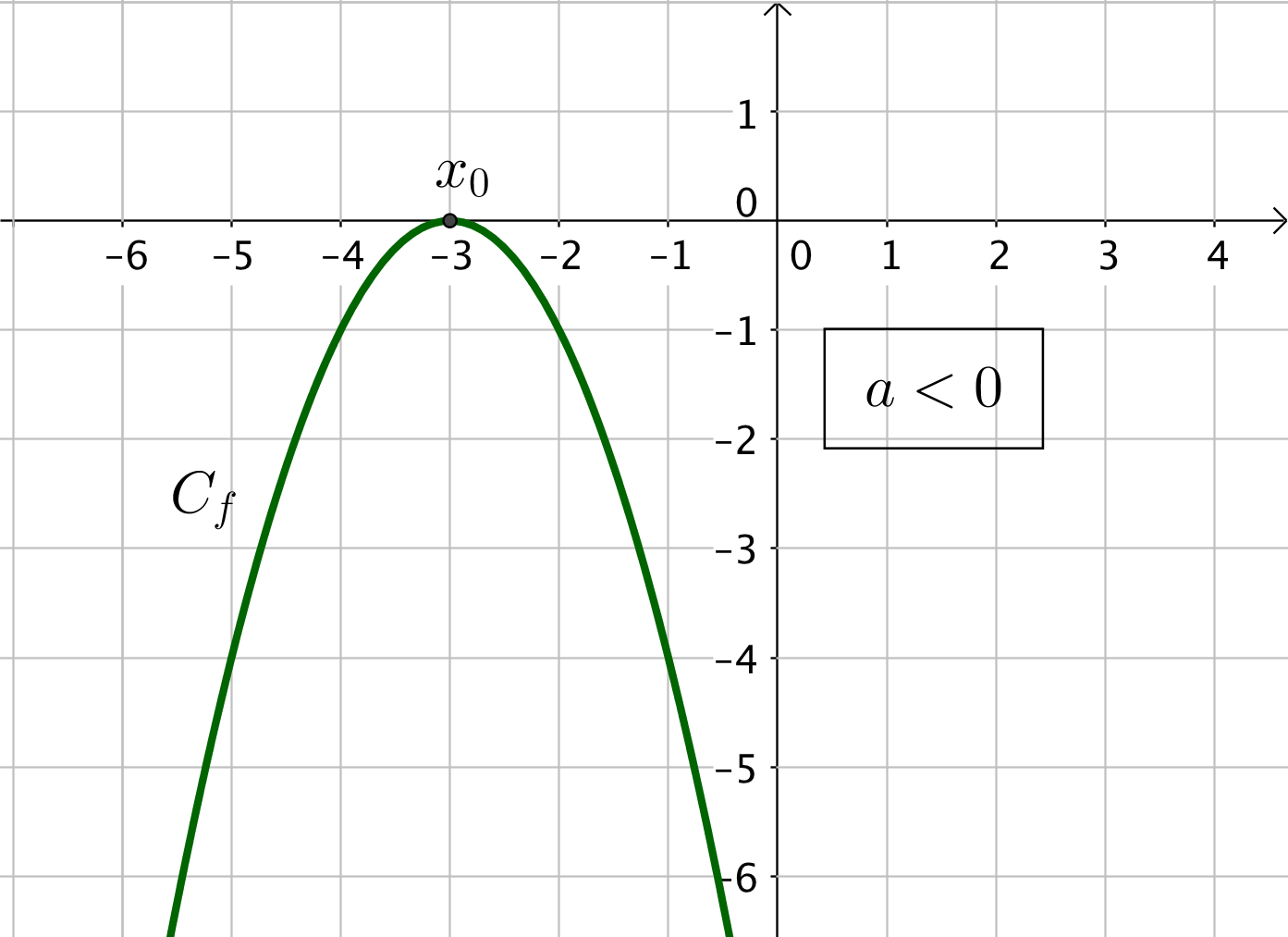
Dans les deux cas, la courbe est tangente à l’axe des abscisses en un point $x_0 = \dfrac{-b}{2a}$.
Si $a > 0$, alors les deux cases du tableau contiennent un signe $+$.
Si $a < 0$, alors les deux cases du tableau contiennent un signe $-$.
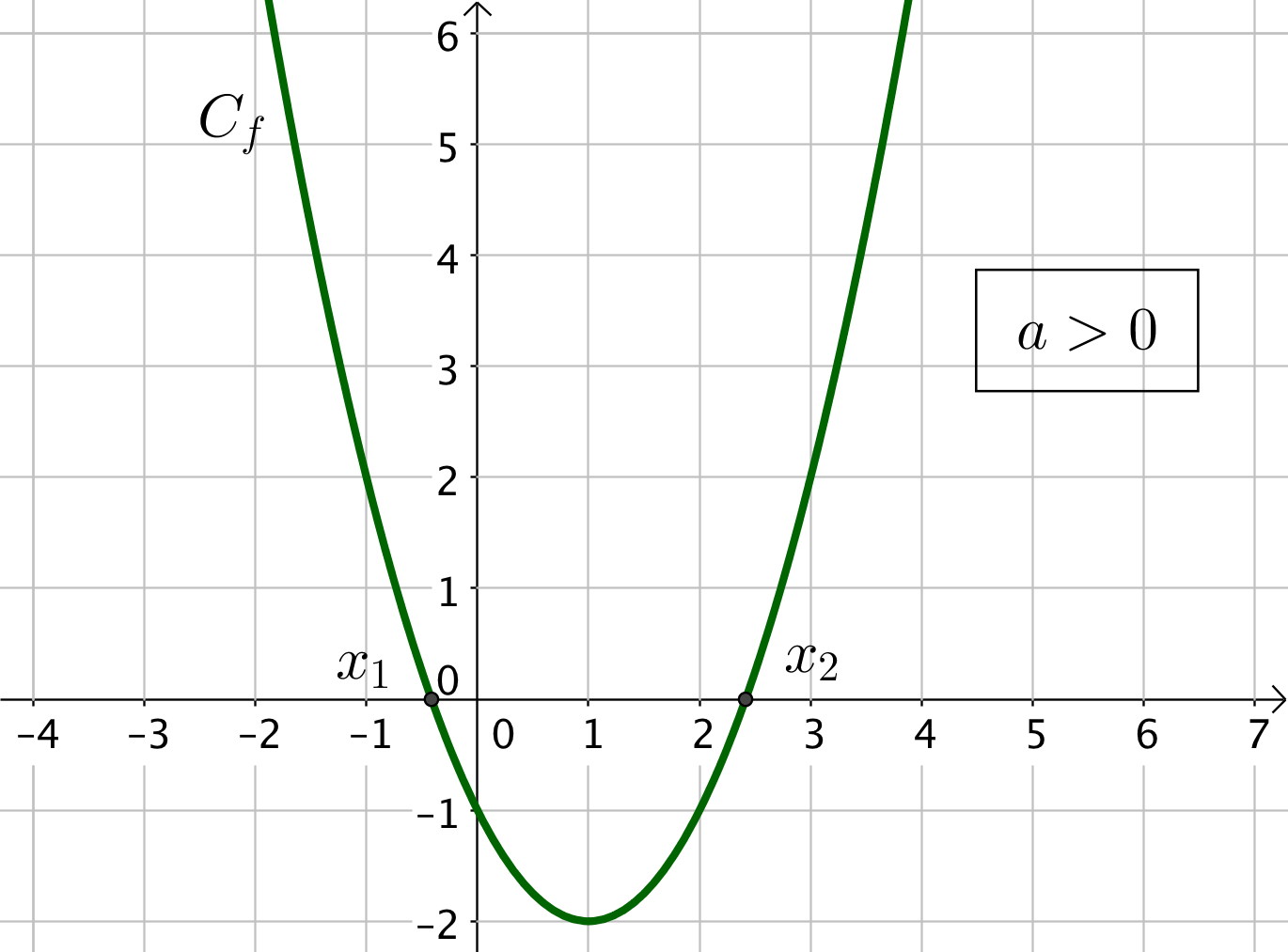
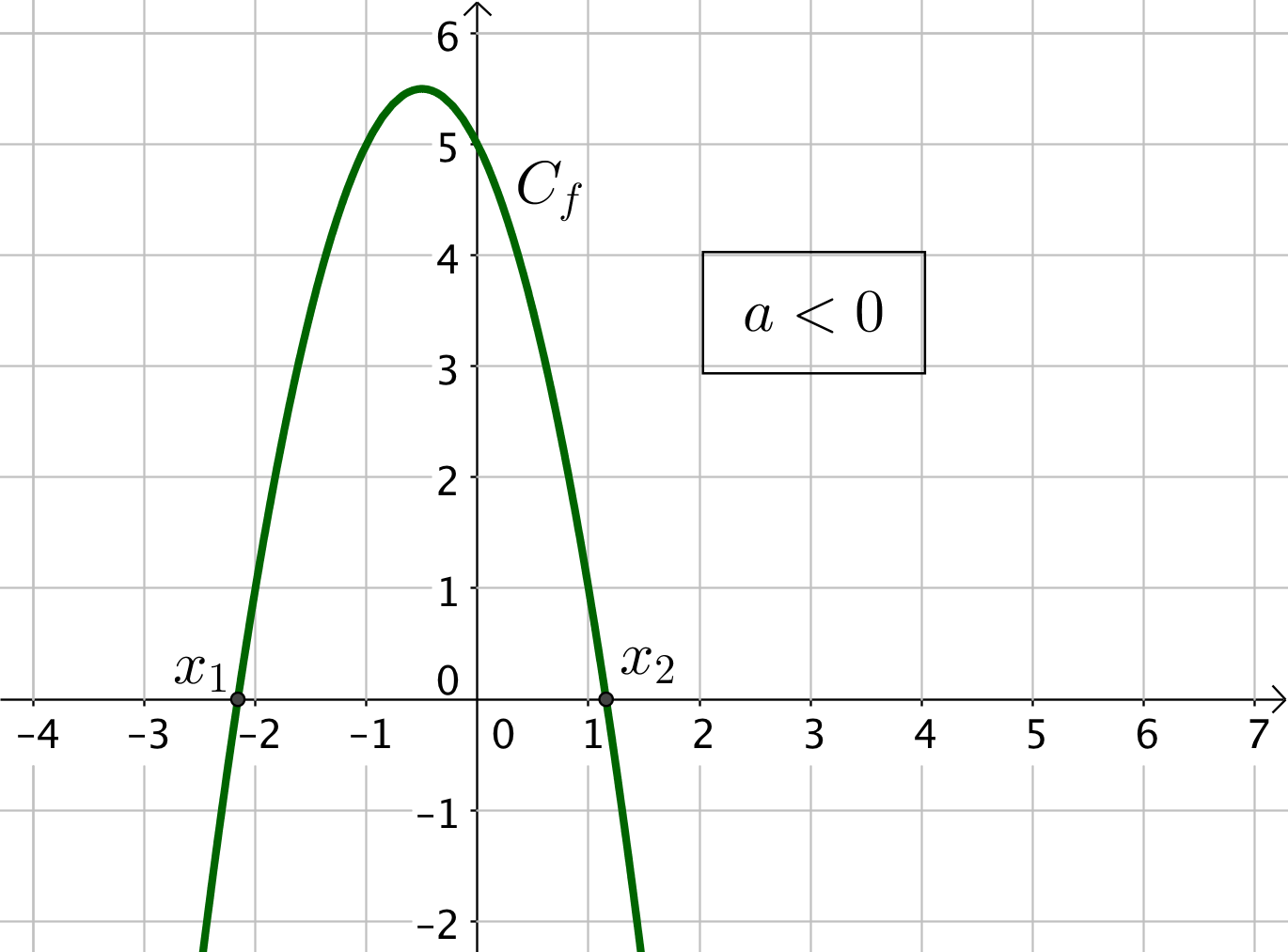
3) Cas où $\Delta > 0$
Le trinôme admet deux racines tels que $x_1 < x_2$.
On indique dans le tableau l’endroit où le trinôme s’annule.
A l’extérieur des racines, le trinôme est du signe de $a$, et à l’intérieur, le trinôme est du signe opposé à $a$.