Discriminant, solutions
Discriminant, solutions
Un polynôme du second degré s’écrit $ax^2 + bx + c$, avec $a \neq 0, b, c \in \mathbb{R}$.
Un outil interessant pour l‘étude des racines d’un polynôme du second degré est le discriminant $\Delta$, défini par $\Delta = b^2 – 4ac$.
Il faudra faire attention aux signes (si par exemple $b = -3,$ alors $ b^2 = (-3)^2 = 9$) : on pourra alors utiliser des parenthèses pour se prémunir d’erreurs de calculs.
Le nombre de racines dépend du signe du discriminant. Il existe 6 cas différents selon le signe de $a$ et celui de $\Delta$.
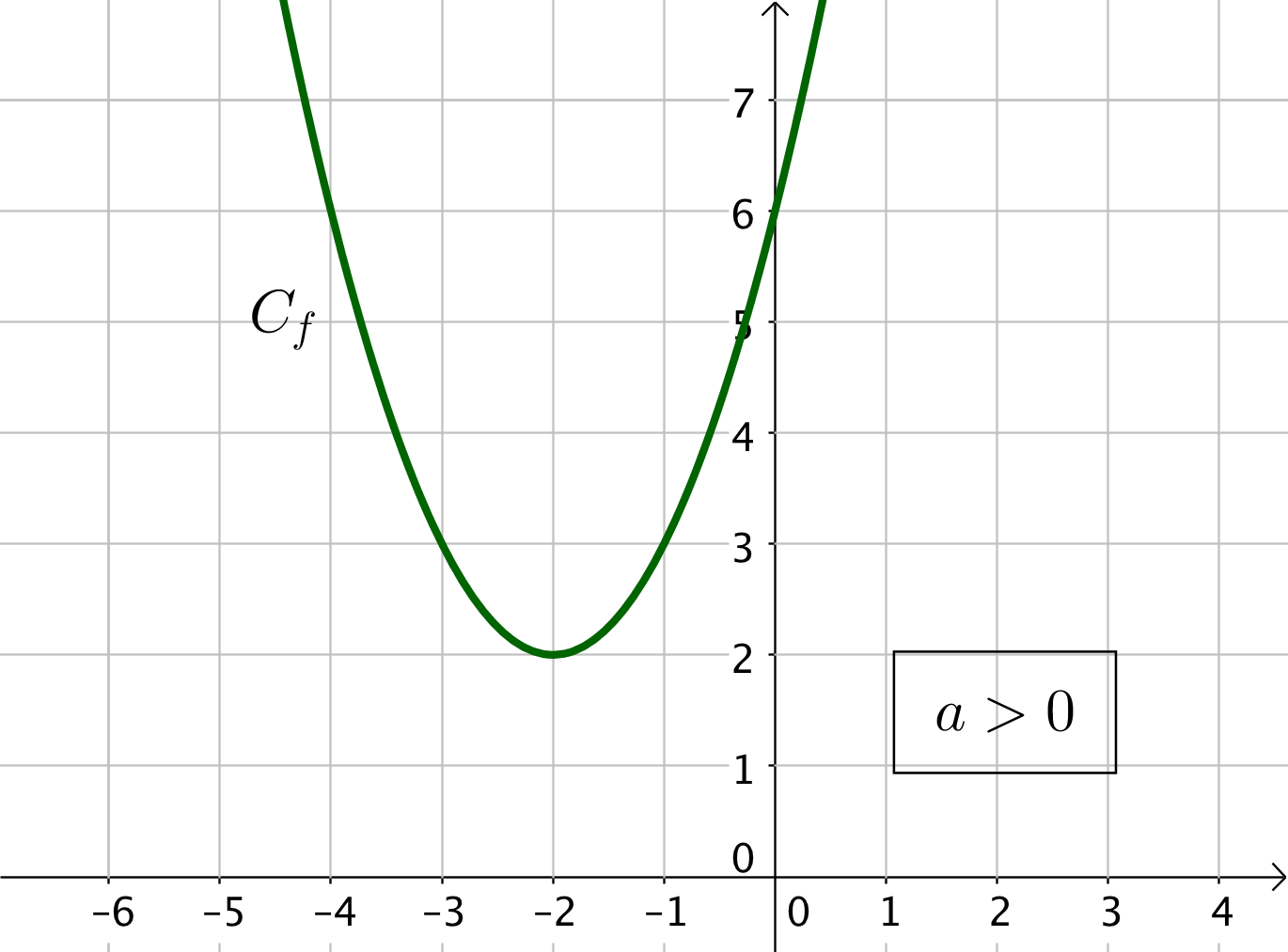
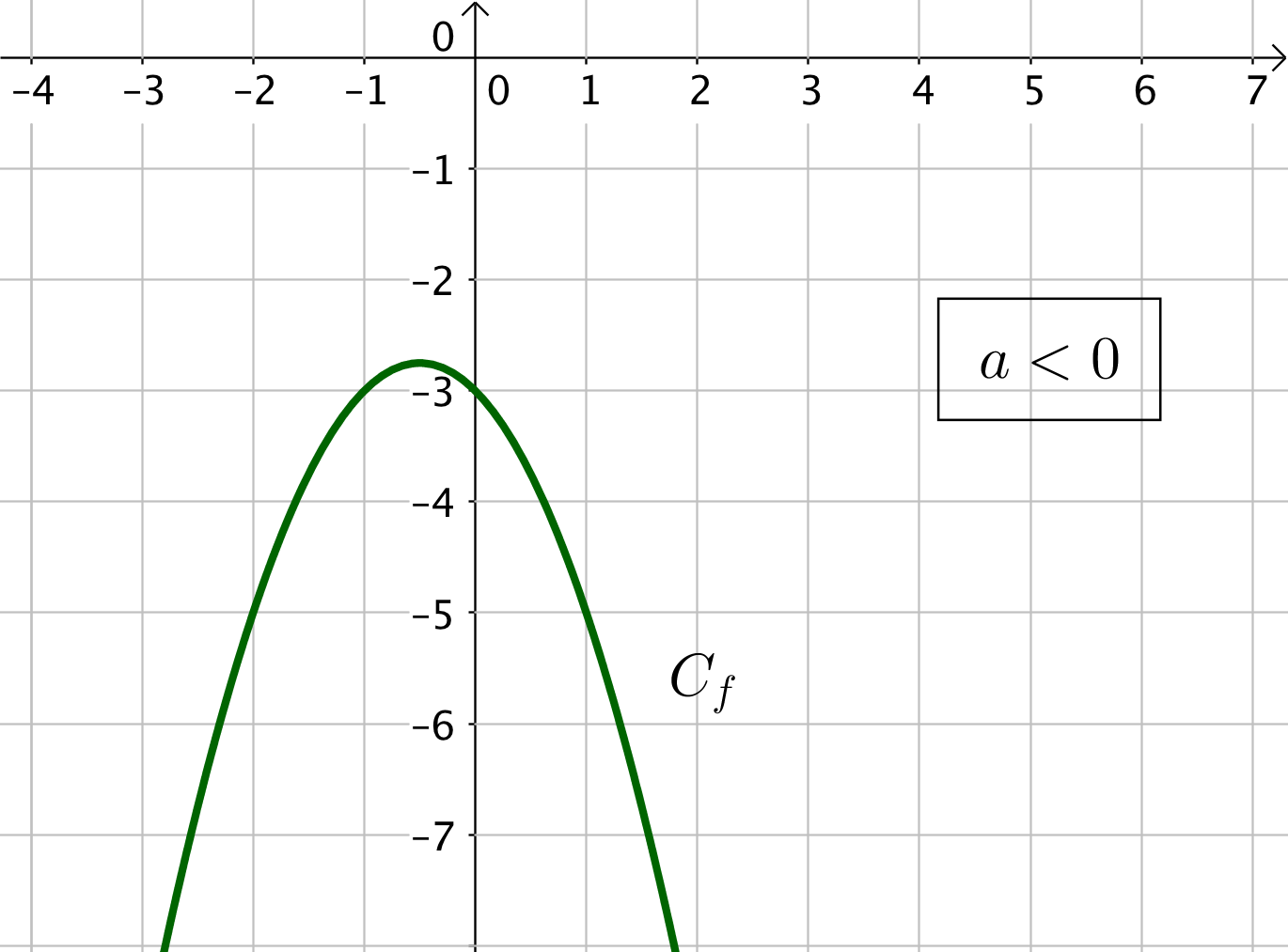
1) Si $\Delta < 0$, la parabole est tournée vers le haut (car $a > 0$) ou vers le bas (si $a < 0$) et il n’y a pas de racine (car $\Delta < 0$).
 |
 |
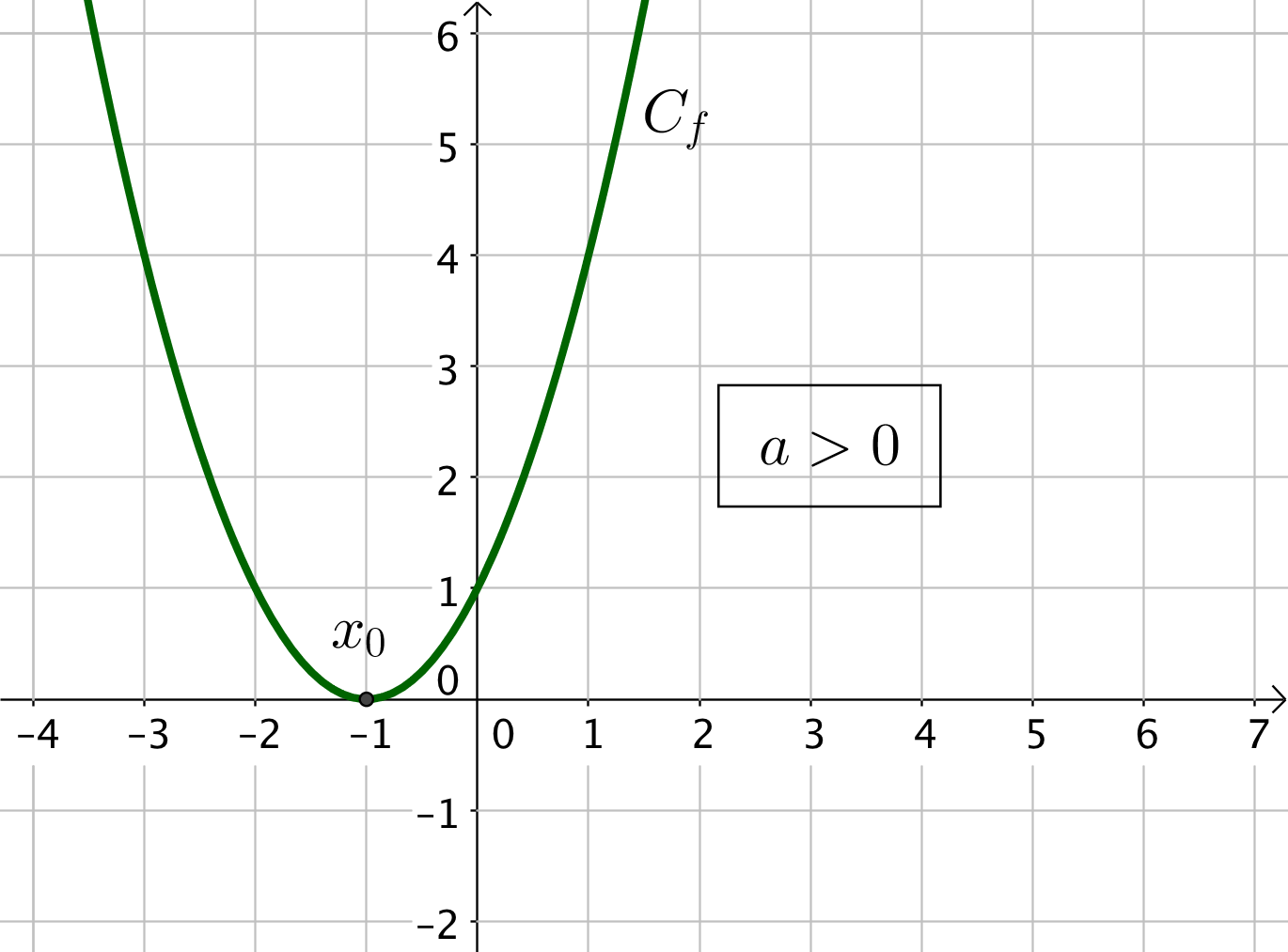
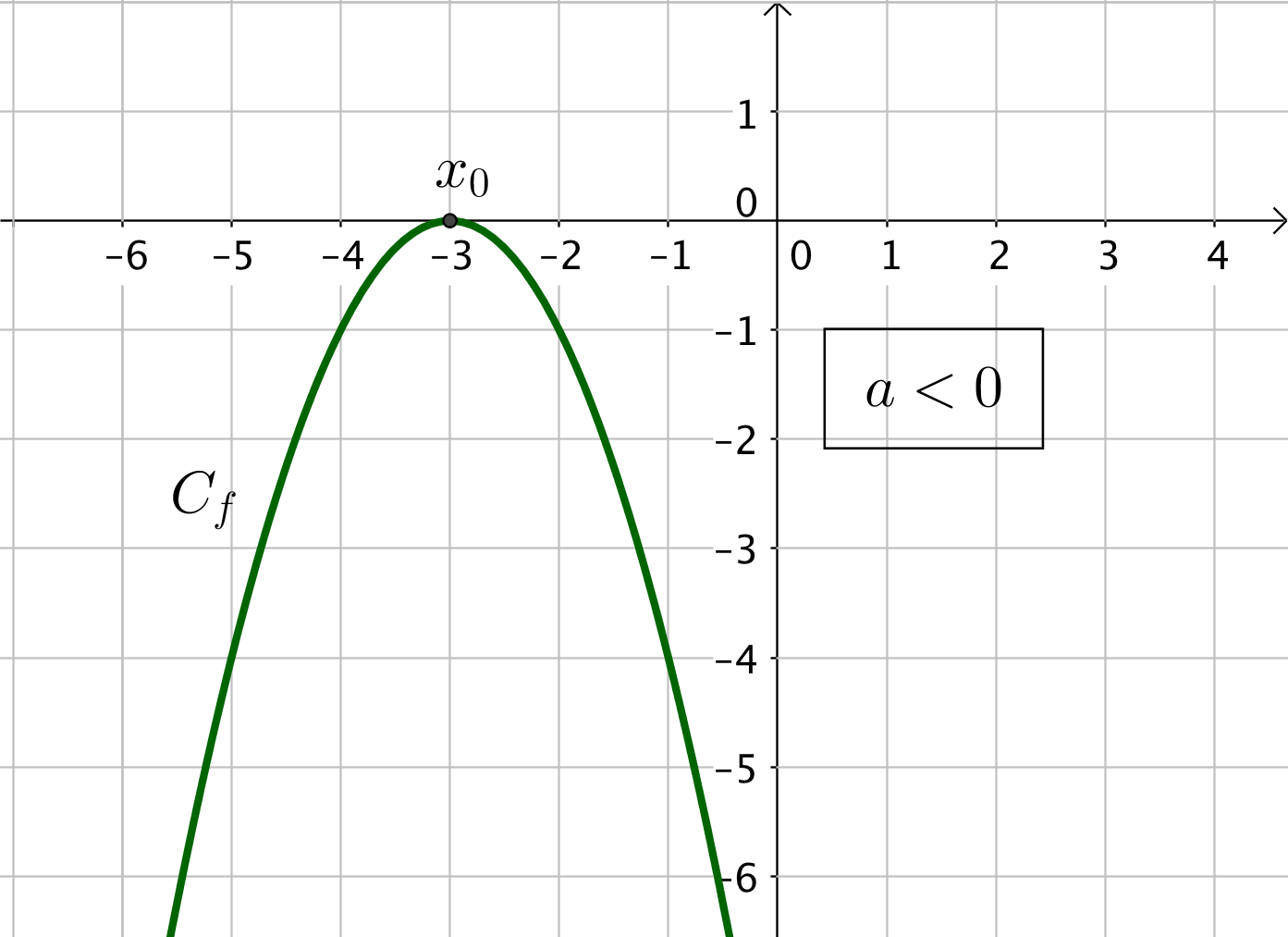
2) Si $\Delta = 0$, l’équation $f(x) = 0$ admet une unique solution : $f$ possède une seule racine $x_0 = \dfrac{-b}{2a}$. La parabole touche l’axe des abscisses en un seul point.
 |
 |
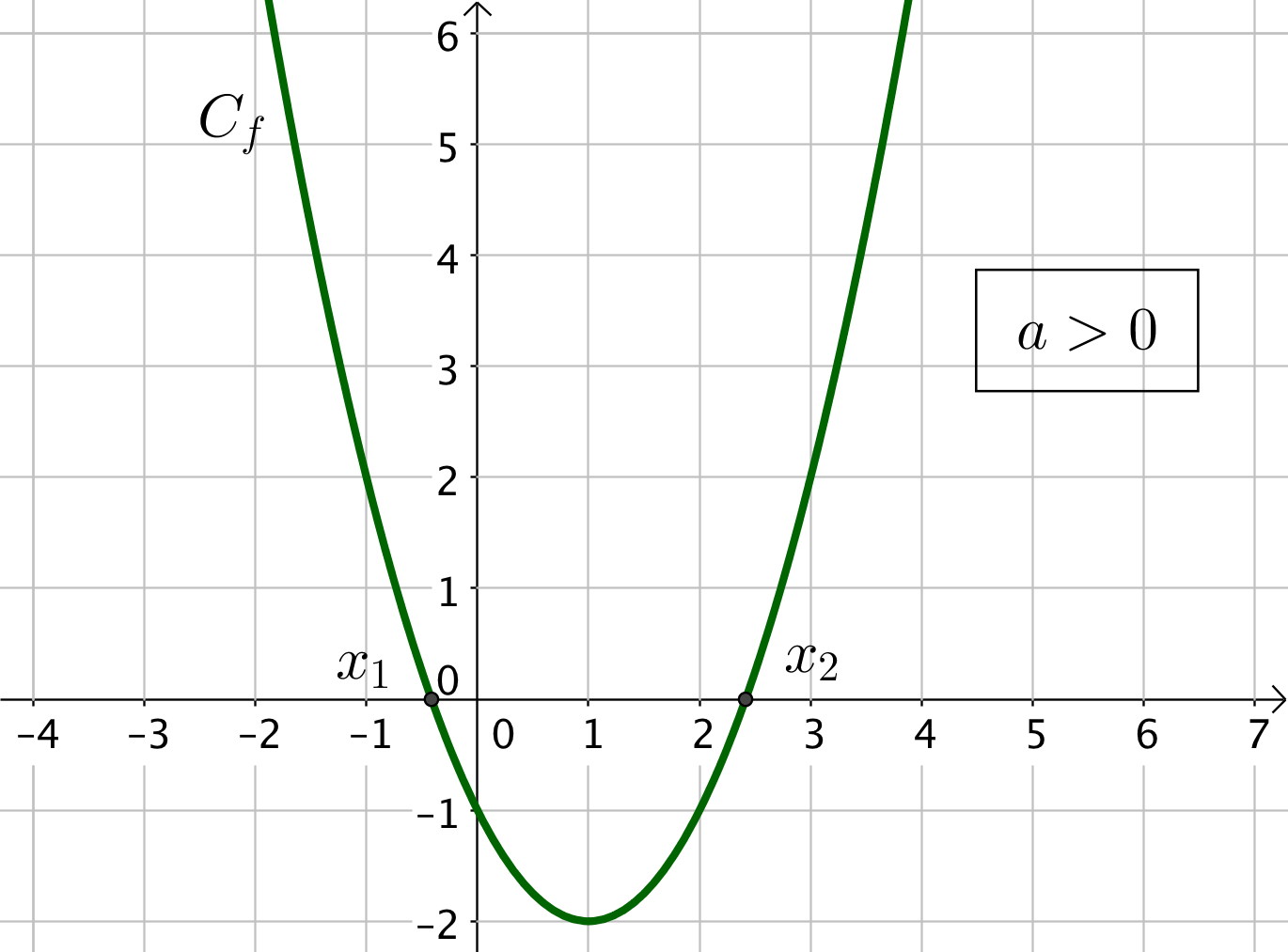
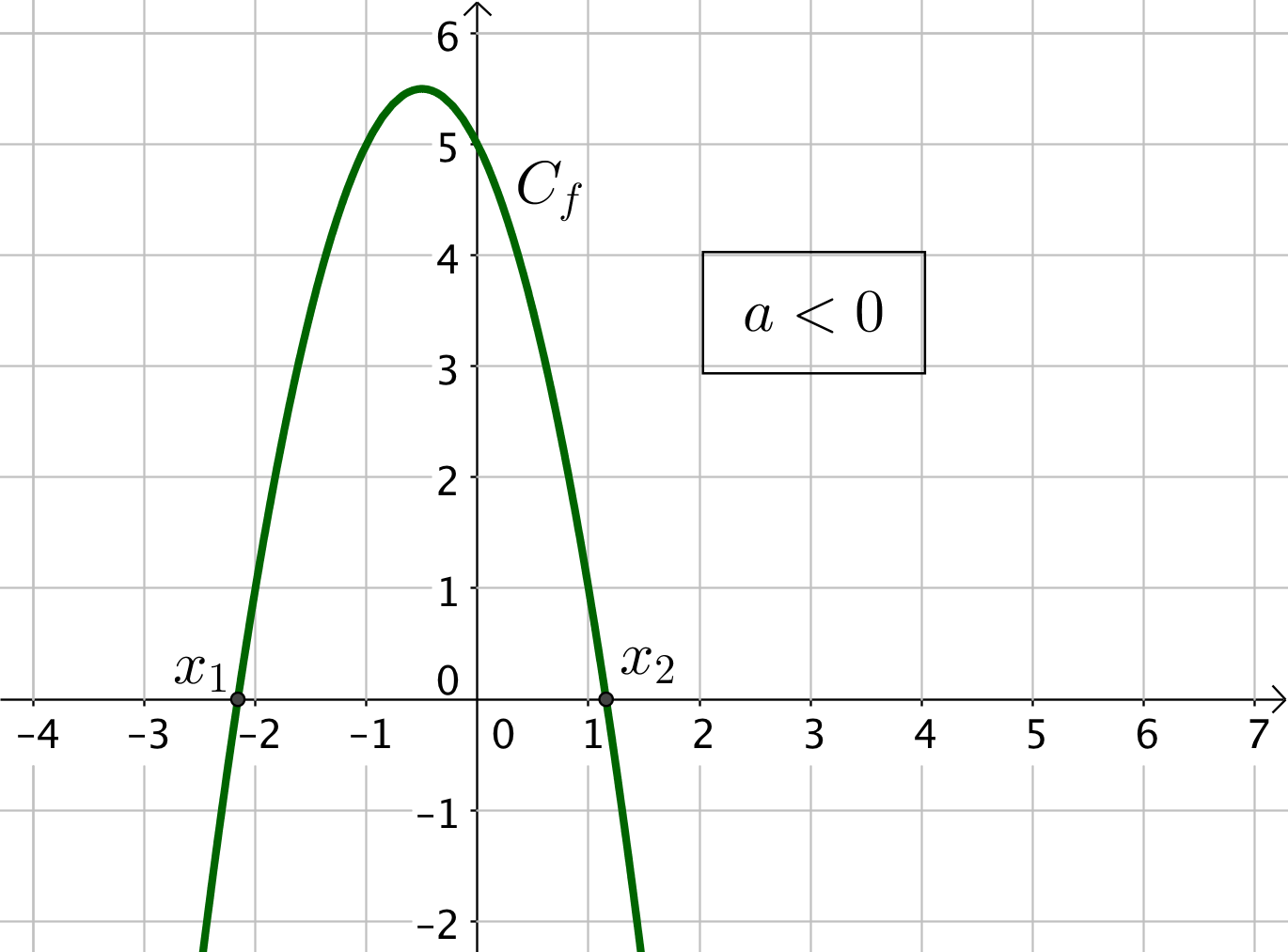
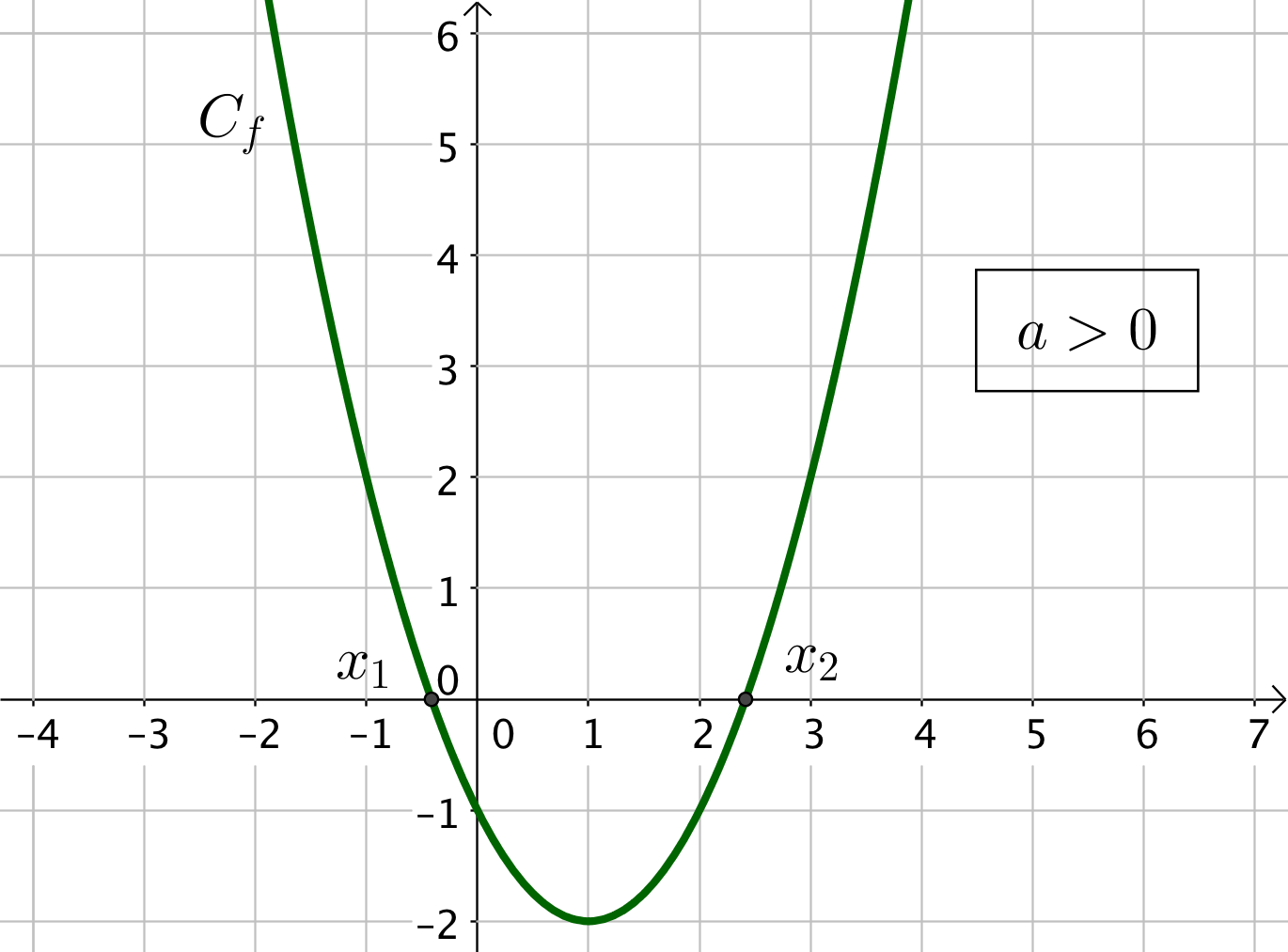
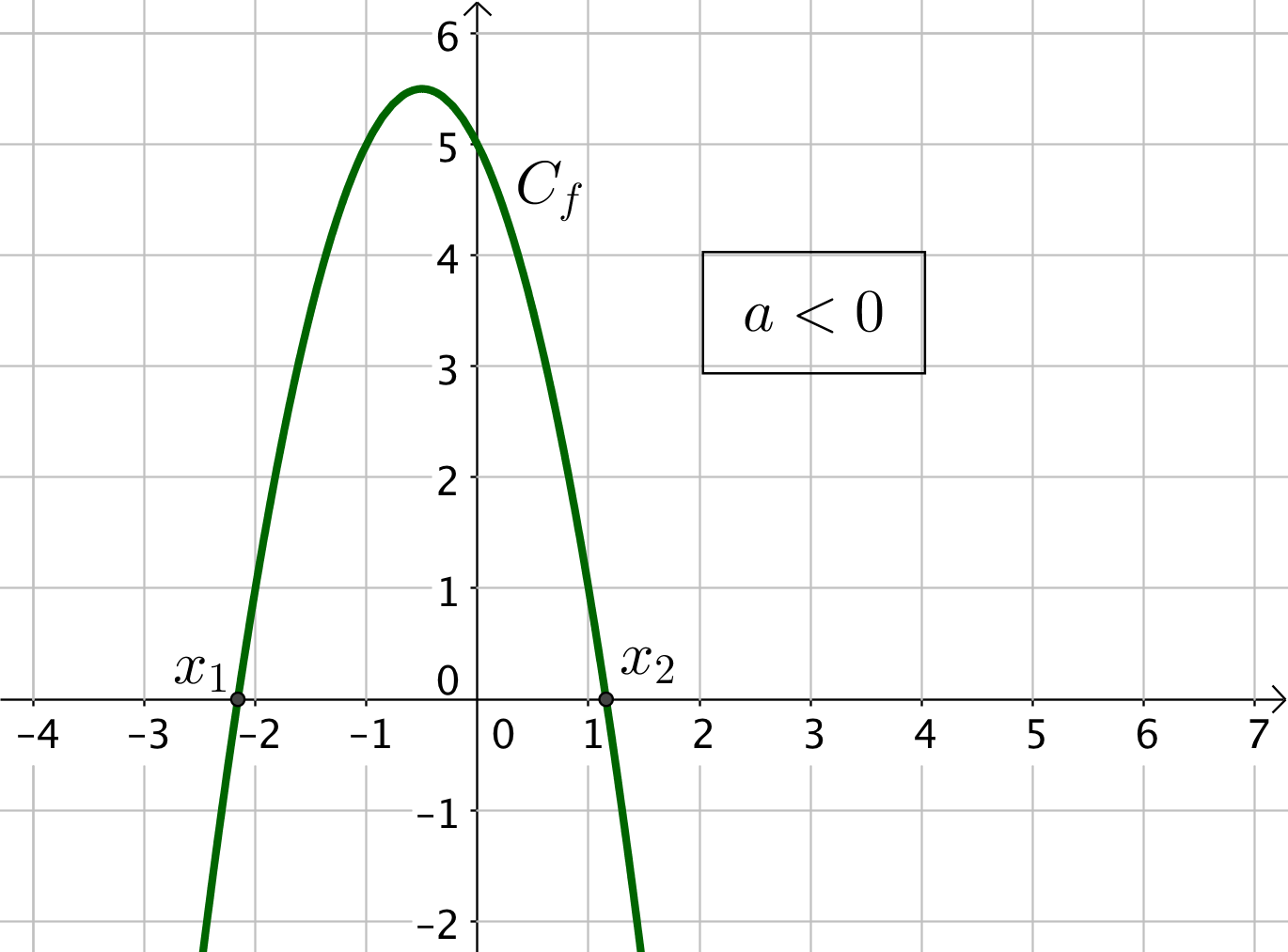
3) Si $\Delta > 0$, l’équation $f(x) = 0$ admet deux solutions : $f$ possède deux racines $x_1 = \dfrac{-b – \sqrt{\Delta}}{2a}$ et $x_1 = \dfrac{-b + \sqrt{\Delta}}{2a}$
 |
 |
Forme canonique
Forme canonique
Une fonction polynomiale de degré 2 définie sur $\mathbb{R}$ s’écrit sous la forme $f(x) = ax^2 + bx + c$, avec $a \neq 0$.
Sa représentation graphique est une parabole tournée vers le haut ou le bas selon le signe de $a$.
Cette fonction admet une autre écriture de la forme $f(x) = a(x -\alpha)^2 + \beta$ avec $\alpha, \beta \in \mathbb{R}$ : c’est la forme canonique.
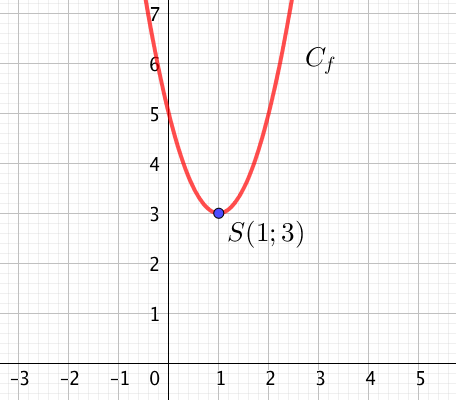
Considérons l’exemple suivant : $f(x) = 2x^2 – 4x + 5$ pour $x \in \mathbb{R}$.
La première étape afin de parvenir à la forme canonique de $f$ consiste à factoriser les termes en $x$ et $x^2$ par $a$.
Ainsi, $f(x) = 2(x^2 – 2x) + 5$. Il faudra prêter une attention particulière au signe de $a$.
Il s’agit maintenant de se remémorer les identités remarquables :
$(a + b)^2 = a^2 + 2ab + b^2$ que l’on réécrit sous la forme $(a + b)^2 – b^2 = a^2 + 2ab$.
Ainsi, $x^2 – 2x$ correspond au début de l’identité remarquable ($a^2 + 2ab$) que l’on réécrit sous la forme $ x^2 – 2 \times 1 \times x$.
Ainsi, $a = x$ et $b = -1$ et on trouve alors $f(x) = 2 \left[(x – 1)^2 – 1\right] + 5$.
Enfin, on réécrit $f$ sous la forme $f(x) = 2(x – 1)^2 – 2 + 5 = 2(x – 1)^2 + 3$. C’est donc la forme canonique, avec $\alpha = 1$ et $\beta = 3$.
Graphiquement, on obtient :
Afin de s’assurer que la forme canonique est correcte, on peut développer à nouveau l’identité remarquable pour retrouver la forme initiale de $f$.
Signe du trinôme
Signe du trinôme
On s’intéresse au signe du trinôme $f(x) = ax^2 + bx + c$, avec $a \neq 0$.
Le discriminant du trinôme est $\Delta = b^2 – 4ac$.
Si la fonction est positive, elle est au dessus de l’axe des abscisses. Si elle est négative, elle est en dessous. La position de la courbe permet donc de connaître le signe de la fonction.
1) Cas $\Delta < 0$ :
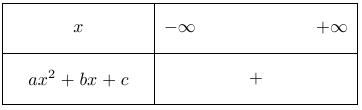
Soit $a>0$ et dans ce cas, la fonction est toujours positive. On indique donc un signe $+$ dans le tableau de signe de la fonction.
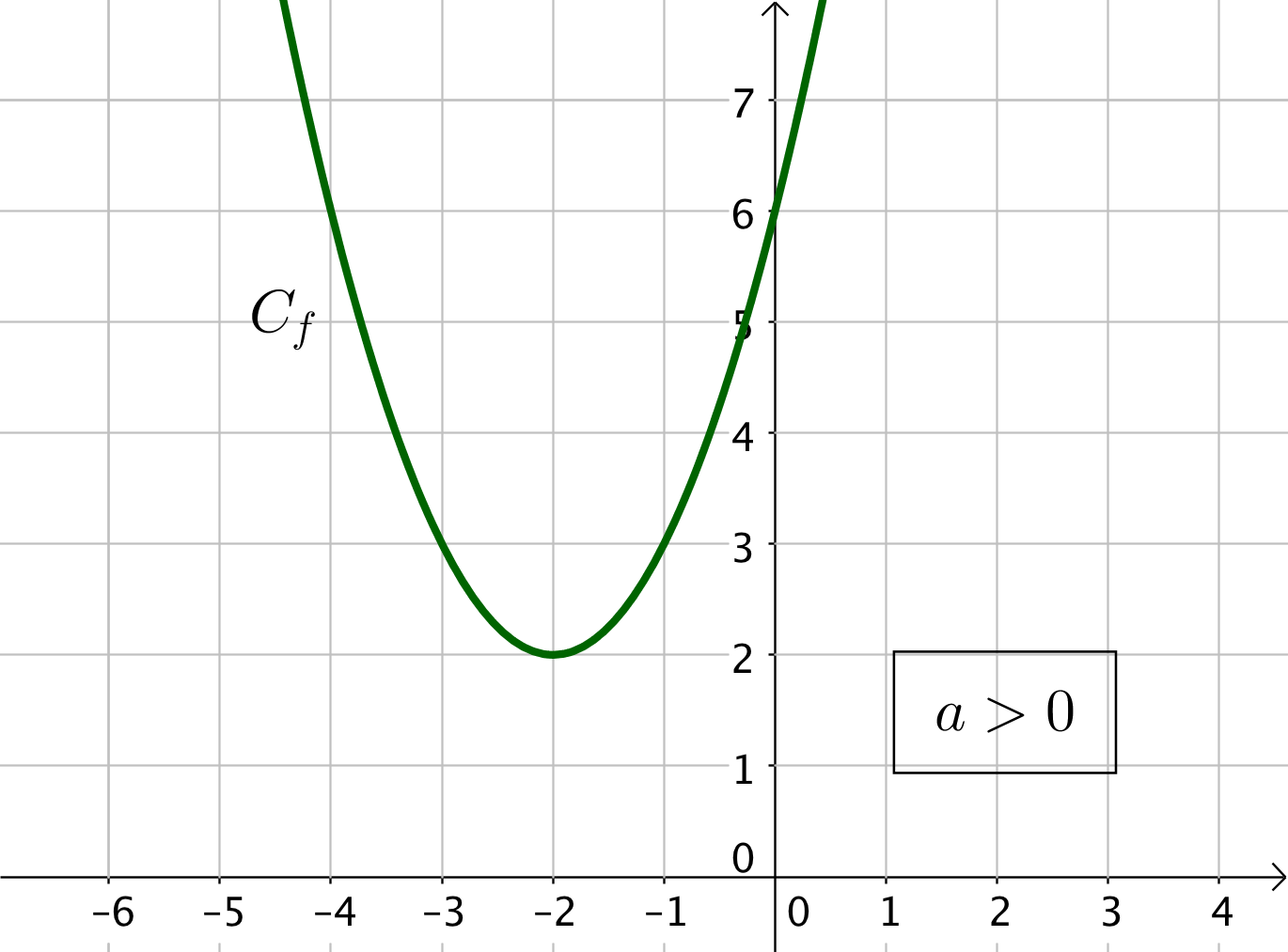
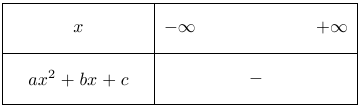
Soit $a < 0$ et la fonction est toujours négative. On indique alors un signe $-$ dans le tableau de signe de la fonction.
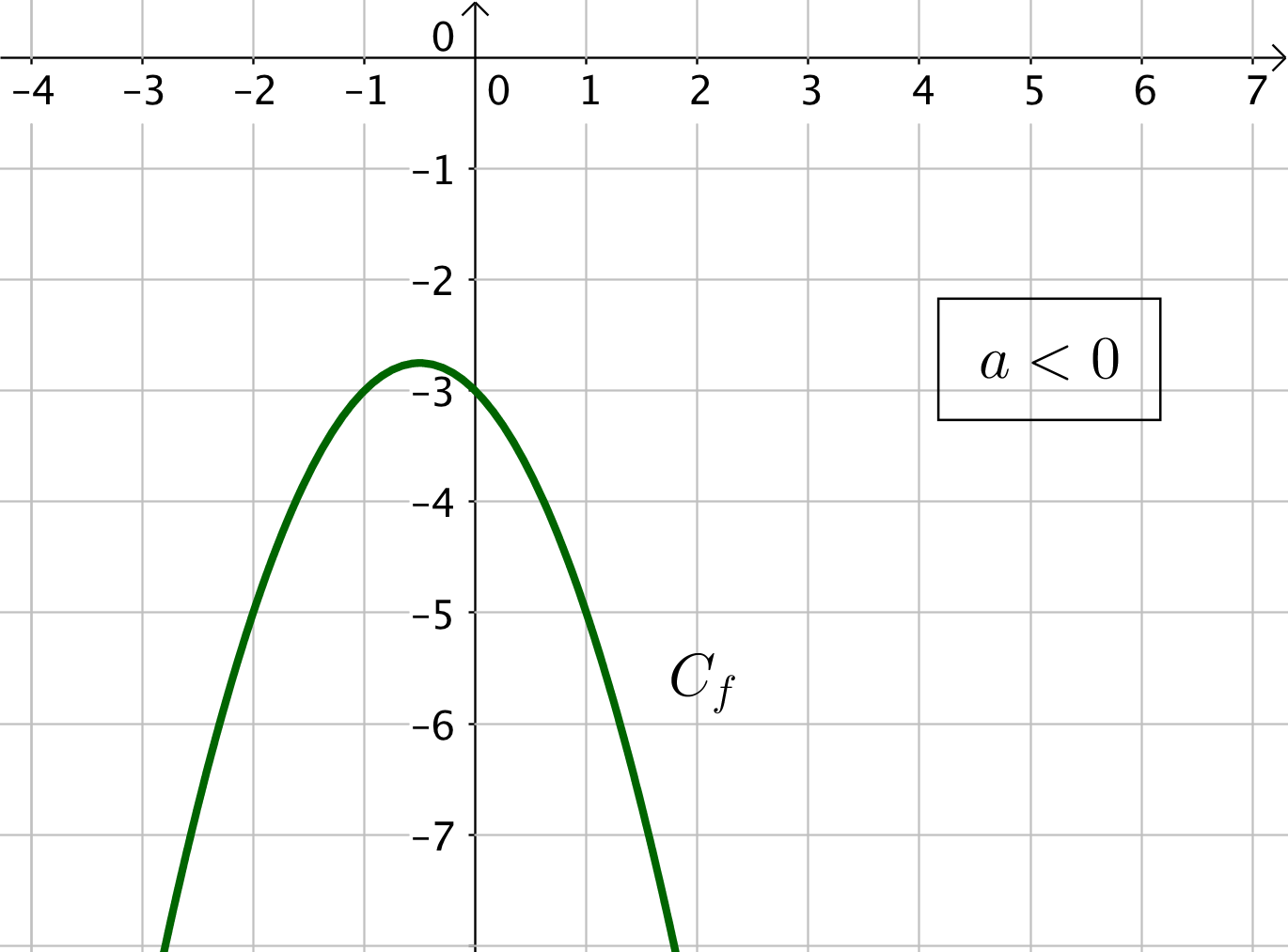
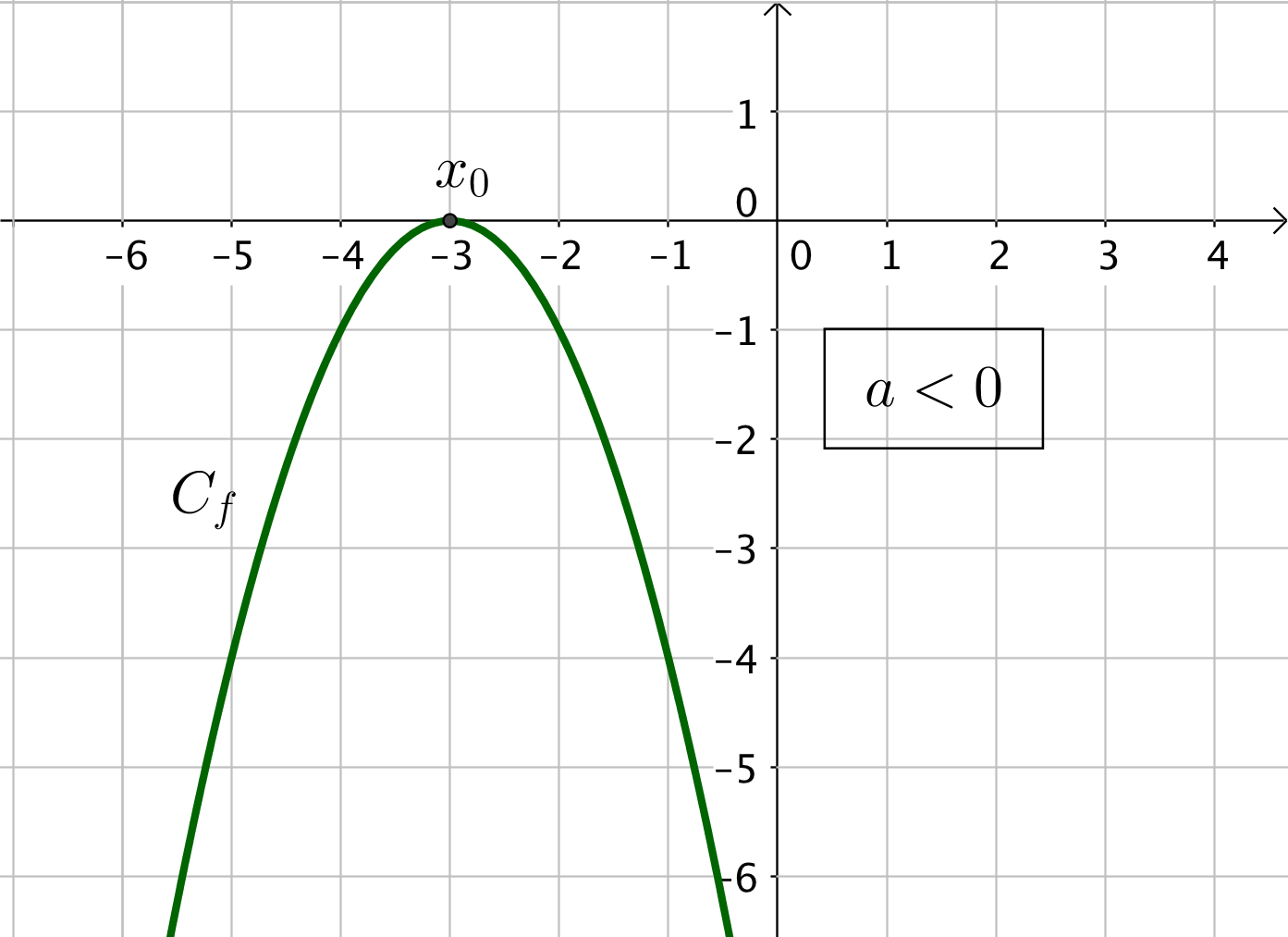
2) Cas où $\Delta = 0$
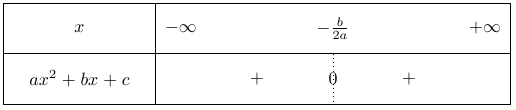
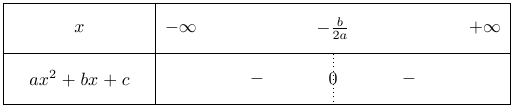
Dans les deux cas, la courbe est tangente à l’axe des abscisses en un point $x_0 = \dfrac{-b}{2a}$.
Si $a > 0$, alors les deux cases du tableau contiennent un signe $+$.
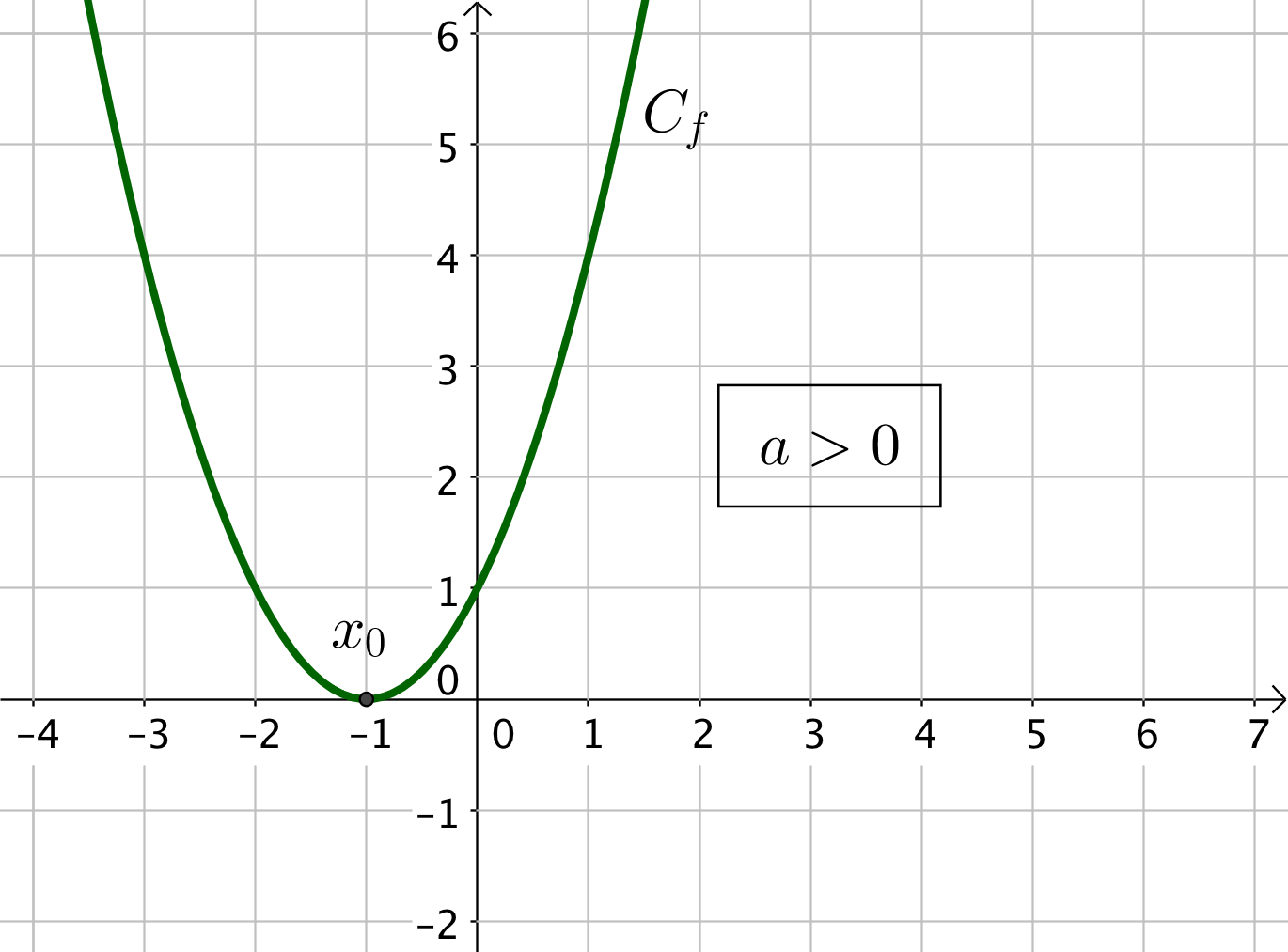
Si $a < 0$, alors les deux cases du tableau contiennent un signe $-$.
3) Cas où $\Delta > 0$
Le trinôme admet deux racines tels que $x_1 < x_2$.
On indique dans le tableau l’endroit où le trinôme s’annule.
A l’extérieur des racines, le trinôme est du signe de $a$, et à l’intérieur, le trinôme est du signe opposé à $a$.