Force conservative
I. Travail d’une force constante sur un chemin rectiligne
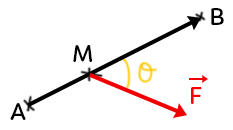
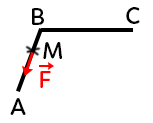
On a une force $\overrightarrow{F}$ qui s’applique au point $M$ et qui se déplace entre les positions $A$ et $B$. On voit que le vecteur $\overrightarrow{AB}$ et le vecteur $\overrightarrow{F}$ forment un angle $\theta$.
Le travail de la force $\overrightarrow{F}$ sur le chemin $AB$ est égal à : $W_{AB}(\overrightarrow{F}) = \overrightarrow{F}.\overrightarrow{AB}=\lVert\overrightarrow{F}\rVert \times \lVert\overrightarrow{AB}\rVert \times cos(\theta)$
II. Force conservative
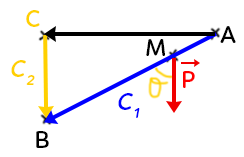
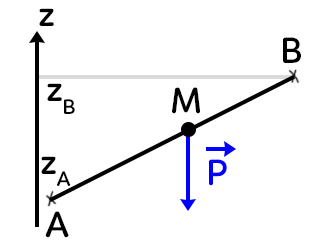
On a le point $M$ qui subit une force $\overrightarrow{P}$ et qui se déplace entre $A$ et $B$.
On a tracé, ici, deux chemins possibles : du point $A$ au point $B$ on peut passer par le chemin bleu noté $C1,$ mais aussi le chemin de $A$ vers $C$ puis vers $B$ noté $C2.$ Il y en a une infinité d’autres mais on en a représenté deux. Une force est dite conservative, si et seulement si, c’est une force dont le travail ne dépend pas du chemin suivi.
Quel que soit le chemin emprunté par le point $M$ pour aller du point $A$ au point $B,$ le travail sera le même.
Par exemple, $\overrightarrow{P} conservatif \iff W_{C1}(\overrightarrow{P} =W_{C2}(\overrightarrow{P}$
III. Cas du poids
On a donc $\overrightarrow{P} = m.\overrightarrow{g}$, avec $\overrightarrow{P}$ la force en Newton (N), m la masse en kilogrammes (kg) et $\overrightarrow{g}$ la constante de pesanteur terrestre qui vaut 9,81 m.s-2.
On va s’intéresser au travail du poids sur les deux chemins précédents.
$W_{C1}(\overrightarrow{P}) = mg\times AB\times cos(\theta)$. L’angle $\theta$ est aussi l’angle $\widehat{CBA}$
On trouve alors une relation trigonométrique : $cos(\theta) = \dfrac{CB}{AB}$
On peut simplifier le calcul : $W_{C1}(\overrightarrow{P}) = mg\times CB$
Maintenant, intéressons-nous à l’autre chemin, en jaune : $W_{C2}(\overrightarrow{P}) = W_{AC}(\overrightarrow{P}) +W_{CB}(\overrightarrow{P})$
Sur $[AC],$ le travail du poids est nul. Sur $[CB]$, on voit que cette fois-ci, les deux vecteurs sont colinéaires. Ils sont parallèles et vont dans la même direction.
On peut écrire le travail du poids sur $[CB]$ comme égal à $mg \times -CB \times cos(0)$
Donc le travail du poids sur $[CB]$ vaut $W_{C2}(\overrightarrow{P}) = mg\times CB$
Ce qui est identique au travail du poids sur $C1$. C’est justement la définition de la force conservative : le travail ne dépend pas du chemin suivi. Le poids est une force conservative.
On peut noter $CB$ comme étant la différence de coordonnées entre les points $A$ et $B$ sur l’axe $z,$ qu’on peut en fait écrire : $W_{AB}(\overrightarrow{P}) = mg(z_A-z_B)$, avec $(z_A-z_B)$ la différence des altitudes.
Force non-conservative
I. Travail d’une force constante sur un chemin rectiligne
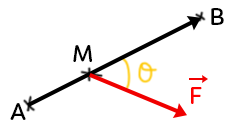
On a un point $M$ qui se déplace du point $A$ au point $B$ et, ce point $M,$ subit une force $\overrightarrow{F}$ avec un angle $\theta$ par rapport au vecteur $\overrightarrow{AB}$.
Dans ce cas-là, le travail de la force $\overrightarrow{F}$ sur $[AB]$ est égal à : $W_{AB}(\overrightarrow{F}) = \overrightarrow{F}.\overrightarrow{AB}$.
II. Force non conservative
Il est conseillé d’aller voir le cours sur les forces conservatives étant donné que la définition de la force non conservative est l’opposé de celle de la force conservative.
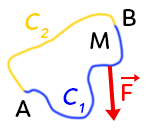
On va considérer le déplacement du point $M,$ du point $A$ au point $B.$ Ce déplacement, on va supposer qu’il peut se réaliser selon deux chemins : le chemin $C1$ et le chemin $C2.$ Le point $M$ subit une force $\overrightarrow{F}$.
Une force est non conservative, si et seulement si, le travail de cette force dépend du chemin choisi.
C’est-à-dire : $\overrightarrow{F} non conservative \iff W_{C1}(\overrightarrow{F}) \ne W_{C2}(\overrightarrow{F})$.
III. Exemple de travail de forces non conservatives
Il existe deux principaux exemples :
– Les frottements fluides sont par exemple les frottements lorsque l’on se déplace à vélo et qu’il y a de l’air qui passe à côté. Cela va ralentir la progression. De la même manière, les frottements fluides sont ce qui permet au parachutiste de ne pas s’écraser au sol. Ces frottements ralentissent le mouvement.
– Les frottements solides sont les frottements lorsqu’on déplace un objet sur une table. Il va y avoir des frictions entre l’objet déplacé et le solide sur lequel on déplace l’objet.
IV. Calcul du travail d’une force de frottement
On a considéré un chemin qui va du point $A$ au point $C$ en passant par le point $B.$
On a deux chemins rectilignes : $A$ vers $B$ et $B$ vers $C.$ On considère le déplacement du point $M$ sur lequel agit une force $\overrightarrow{F}$. Cette force est toujours opposée au déplacement.
On va considérer que $\lVert\overrightarrow{F}\rVert = 50N$, $\lVert\overrightarrow{AB}\rVert = 1m$, $\lVert\overrightarrow{BC}\rVert = 2m$.
On peut donc calculer le travail de la force de frottements, le travail de la force non conservative sur le chemin $[AC]$ :
$W_{AC}(\overrightarrow{F})= W_{AB}(\overrightarrow{F})+W_{BC}(\overrightarrow{F})$
$= \overrightarrow{F}.\overrightarrow{AB}+\overrightarrow{F}.\overrightarrow{BC}$
$= \lVert\overrightarrow{F}\rVert\times \lVert\overrightarrow{AB}\rVert\times cos(\theta)+ \lVert\overrightarrow{F}\rVert\times \lVert\overrightarrow{BC}\rVert \times cos(\theta)$
$= 50\times 1 \times cos(180°)+50\times 2\times cos(180°)$. $W_{AC}(\overrightarrow{F}) $
$= -150N$
Si on avait considéré un autre chemin, le travail aurait été différent. Ce qui est bien la définition d’une force non conservative.
Energie potentielle
I. Définition
On s’intéresse à la force $P$ s’appliquant sur le point $M$ qui se déplace de $A$ à $B.$ L’énergie potentielle est exclusivement associée à une force conservative. On pourra donc associer une énergie potentielle $Ep$ à toute force conservative. La variation d’énergie potentielle se définit par :
$\Delta (Ep) = Ep(B)- Ep(A) = – WAB(P) = – m \times g \times (z_A- z_B) = m \times g \times (z_B-z_A)$
Le signe négatif vient du sens de $P$ qui est opposé à l’axe $z.$ On peut exprimer le poids en fonction de la masse et de la force de la gravitation.
II. Pas d’erreur de signe
Si l’altitude augmente dans le cas de l’énergie potentielle, alors cette dernière augmente et $\Delta Ep > 0$.
Si l’altitude diminue alors l’énergie potentielle diminue et $\Delta Ep < 0$.
$m$ et $g$ sont toujours positifs.