Le travail d'une force constante
Le travail d’une force est l’énergie fournie par cette force lorsque son point d’application se déplace. Il est responsable de la variation d’énergie cinétique.
Par exemple, en poussant un chariot, on exerce une force sur ce dernier qui se déplace alors d’un point $A$ à un point $B$. Le travail de cette force correspond donc bien à une énergie que l’on a fourni pour le déplacer. En mettant ainsi le chariot en mouvement, la vitesse de ce dernier évolue, modifiant son énergie cinétique, d’expression $E_c = \dfrac{1}{2} m v^2$, avec $m$ la masse du système et $v$ sa vitesse.
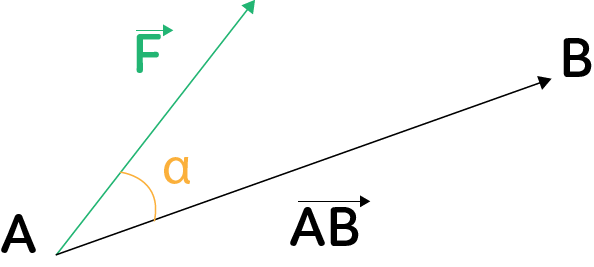
Le travail d’une force d’un point $A$ à un point $B$ est donc une énergie (exprimé donc en Joule) et se note $W_{AB}(\overrightarrow{F})$.
Considérons le mouvement d’un système d’un point $A$ à un point $B$ et une force $\overrightarrow{F}$ constante qui s’exerce dans une direction quelconque, formant ainsi un angle $\alpha$ avec $\overrightarrow{AB}$, alors $W_{AB}(\overrightarrow{F}) = F \times AB \times \cos(\alpha)$, avec $F = \|\overrightarrow{F}\|$, l’intensité de la force et $AB = \|\overrightarrow{AB}\|$.
Il existe trois situations à connaître :
1. Le travail du poids
On considère qu’on lâche dans un premier temps un objet entre $A$ et $B$ :
$W_{AB}(\overrightarrow{P}) = P \times AB \times 1$, car l’angle entre $\overrightarrow{F}$ et $\overrightarrow{AB}$ est nul.
Ainsi, en remplaçant $P$ par sa valeur, on obtient $W_{AB}(\overrightarrow{P}) = mg \times AB$, qui rappelle l’énergie potentielle de pesanteur d’un système où $AB = h$, avec $h$ l’altitude. Le travail étant positif, c’est un travail moteur.
En supposant maintenant qu’on lance l’objet de $B$ vers $A$, le poids s’oppose alors au mouvement : le travail est alors résistant, le travail étant négatif. Il existe en outre un angle de $180°$ entre $\overrightarrow{F}$ et $\overrightarrow{AB}$, ainsi $\cos(\alpha) = \cos(180) = -1$ : $W_{AB}(\overrightarrow{P}) = -mg \times AB$.
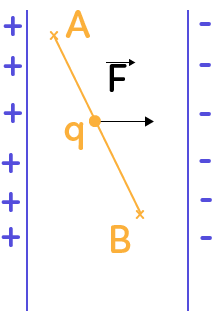
2. Le travail d’une force électrique
On considère ici une particule chargée se déplaçant entre deux point $A$ et $B$ situés entre deux armatures métalliques parallèles (un condensateur) où le champ est constant, le travail de la force $\overrightarrow{F}$ est donc :
$W_{AB}(\overrightarrow{F}) = q \times U_{AB}$, avec $q$ la charge de la particule et $U_{AB}$ la tension entre le point $A$ et le point $B$.
3. Le travail des forces de frottement
En poussant un objet, il est possible de constater une résistance liée aux frottements qui exercent donc un travail résistant calculé par : $W_{AB}(\overrightarrow{f}) = -f \times AB$, avec $AB$ la distance parcourue.
Le poids et la force électrique sont des forces conservatives. Lorsque le système n’est soumis qu’à des forces conservatives, l’énergie mécanique ne varie pas.
En outre, le travail d’une force conservative ne dépend pas du trajet parcouru entre les points $A$ et $B$. Pour le travail du poids par exemple, seul importe la variation d’altitude.
Le travail des forces de frottement dépend du chemin parcouru : ces forces ne sont pas conservatives.
Énergies cinétique, potentielle et mécanique
Rappels
Quand on étudie un mouvement il faut bien définir le référentiel, c’est l’objet de référence par rapport auquel on étudie le mouvement. Il faut associer à l’étude du mouvement un repère d’espace qui permet de connaître la position de notre objet d’étude et une horloge qui permet de mesurer le temps, et d’associer le temps à l’espace.
Énergie cinétique
L’énergie liée au mouvement est l’énergie cinétique, c’est l’énergie que possède un corps du fait de son mouvement. Sa définition est \(Ec= \frac{1}{2} mv^2.\)
\(m\) : la masse de l’objet étudié (kg)
\(v\) : la vitesse (m/s)
\(Ec\) : l’énergie cinétique (J)
Par définition l’énergie cinétique est toujours positive, ce que nous intéresse c’est la variation d’énergie cinétique, qui pourra être positive ou négative.
La variation d’énergie cinétique :
\(\Delta Ec= Ecf-Eci= \frac{1}{2} m v_f^2 – \frac{1}{2} mv_i^2\)
\(\Delta Ec>0\) le corps accélère.
\(\Delta Ec<0\) le corps ralentit.
Remarque importante :
Pour passer des km/h aux m/s, il faut diviser par 3,6.
Pour passer des m/s aux km/h, il faut multiplier par 3,6.
Énergie potentielle de pesanteur
Elle est liée à l’altitude. Plus l’altitude est élevée et plus on a une énergie potentielle de pesanteur. On va mesurer l’altitude d’un objet d’étude en fonction d’une référence. Il faut absolument avoir une référence, une altitude zéro, pour pouvoir déterminer quelle est la hauteur de l’objet d’étude.
\(Epp=mgz_G\)
\(m\) : la masse de l’objet étudié (kg)
\(g\) : l’intensité de la pesanteur (N/Kg)
\(z_G\) : l’altitude du centre de gravité (m)
Epp : énergie potentielle de pesanteur (J)
La variation d’énergie potentielle de pesanteur :
\(\Delta Epp=mgz_{Gf} -mgz_{Gi}\)
\(\Delta Epp>0\) le corps s’élève.
\(\Delta Epp<0\) le corps se baisse. \(g = 9,81\) N kg-1
Énergie mécanique
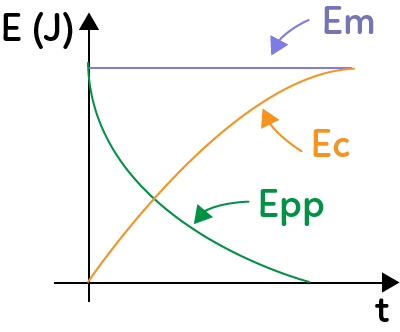
L’énergie mécanique est $Em$ et vaut par définition \(Em=Ec+Epp\).
Si pas de frottements :
\(Em=cte\)
\(\Delta Em=0\)
Avec une énergie mécanique constante, on dit que l’énergie se conserve. On a une énergie potentielle de pesanteur qui diminue, une énergie cinétique qui augmente et quand on fait la somme de l’énergie potentielle de pesanteur et de l’énergie cinétique, on a une valeur constante de l’énergie mécanique. Ces tracés sont obtenus dans le cas d’une chute car l’énergie potentielle de pesanteur diminue comme l’altitude diminue et l’énergie cinétique augmente car la vitesse augmente lors d’une chute.
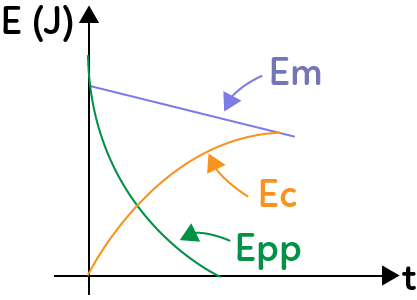
Si frottements :
\(Em\neq cte\)
\(\Delta Em \neq 0\)
On a des frottements donc on se rend compte que, progressivement, la somme de l’énergie cinétique et de l’énergie potentielle de pesanteur diminue. La différence entre l’énergie mécanique au départ et l’énergie mécanique à un instant $t$ correspond à l’énergie qui a été dissipée sous forme d’agitation thermique du fait des frottements.
Théorème de l'énergie cinétique
I. Énergie cinétique et travail
Énergie cinétique
$E_c = \dfrac{1}{2} \times m \times v^2$
Avec la masse $m$ en kg, la vitesse $v$ en m/s et $E_c$ en J. Cette relation dit que l’énergie cinétique d’un objet est l’énergie mécanique associée au déplacement, à la vitesse $v$ d’un objet ayant une masse $m.$
Travail d’une force constante lors d’un déplacement rectiligne
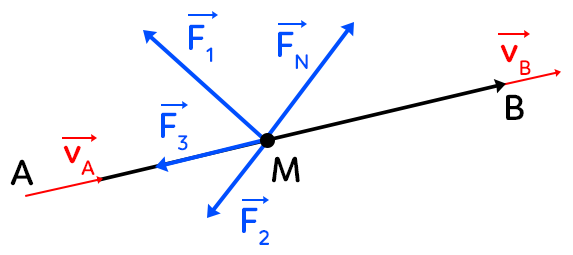
La force ne doit pas varier au cours du déplacement qui doit être rectiligne. Sans ces deux conditions, on ne peut pas (au niveau lycée) effectuer les calculs. Le déplacement de $M$ du point $A$ vers le point $B$ nous intéresse. Tout au long du déplacement, le point $M$ est soumis à la force $F$ constante. Dans ces conditions-là :
$W_{AB}(\overrightarrow{F}) = \overrightarrow{F}.\overrightarrow{AB}=\lVert\overrightarrow{F}\rVert \times \lVert\overrightarrow{AB}\rVert \times cos(\theta)$
Avec $θ$ l’angle entre $AB$ et $F.$
II. Théorème de l’énergie cinétique
Position du problème
$V_A$ est la vitesse du point $M$ en $A$ et $V_B$ la vitesse du point $M$ lorsqu’il arrive en $B.$ Plusieurs forces peuvent s’appliquer au point $M.$
Le théorème
Le théorème dit que :
$E_c (B) – E_c (A) = W_{AB} (\overrightarrow{F_1}) + W_{AB} (\overrightarrow{F_2}) + … + W_{AB} (\overrightarrow{F_N})$
La variation d’énergie cinétique entre le point $B$ et le point $A$ est donc égale à la somme du travail pour chaque force s’appliquant à l’objet. On peut réécrire comme étant :
$\dfrac{1}{2} mv_B^2 – \dfrac{1}{2} mv_A^2 = \overrightarrow{F_1} . \overrightarrow{AB} + \overrightarrow{F_2} . \overrightarrow{AB} + … + \overrightarrow{F_N} . \overrightarrow{AB}$
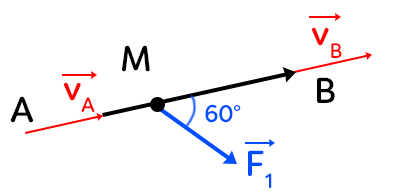
Exemple
$\lVert\overrightarrow{AB}\rVert = 10m$
$\lVert\overrightarrow{F_1}\rVert = 200 N$
$v_A = 0m.s^{-1}$
$m = 10 kg$
$\dfrac{1}{2} mv_B^2 – \dfrac{1}{2} mv_A^2 = \lVert\overrightarrow{F_1}\rVert \times \lVert\overrightarrow{AB}\rVert \times cos θ$