Étude énergétique d’un problème mécanique - Chute libre
La chute libre
On étudie ici la chute de Félix Baumgartner.

On choisit le référentiel géocentrique.
Quelles sont les forces qui s’appliquent sur Félix Baumgartner lorsqu’il saute ?
Les forces qui s’appliquent sur F. Baumgartner lorsqu’il saute sont le poids (vertical vers le bas), dans le même sens que le sens du saut : le travail du poids est donc moteur ; et les frottements de l’air (que l’on néglige dans un premier temps).
On considère les conditions initiales suivantes :
à $t = 0, \left \{ \begin{array}{c}
v_0 = 0 \text{ m.s}^{-1} \\
y_0 = h_0 \\
\end{array}
\right.$
Quelles sont les deux énergies liées à Félix Baumgartner ?
Les deux énergies liées à ce problème sont l’énergie cinétique : $E_c = \dfrac{1}{2} m v^2$, et l’énergie potentielle de pesanteur, liée au travail du poids entre $A$ et $B$, $E_p = mgh$.
En outre, la somme des deux est égale à l’énergie mécanique $E_m$.
Au départ de son saut, F. Baumgartner a une hauteur maximale à $t = 0$, l’énergie potentielle est maximale. Puis lors de sa chute, son altitude diminue, son énergie potentielle aussi.
Au contraire, sa vitesse est nulle au départ puis augmente au cours du temps.
L’énergie mécanique, correspond à la somme des deux, est constante au cours du temps, car la seule force agissant sur le système est le poids qui est une force conservative.
D’abord peu présentes, les molécules de l’atmosphère gagnent en nombre au cours de sa chute : les frottements de l’air ne sont plus négligeables au bout d’un certain temps. Les forces de frottement sont non conservatives, provoquant une stagnation de la vitesse et donc une diminution l’énergie mécanique.
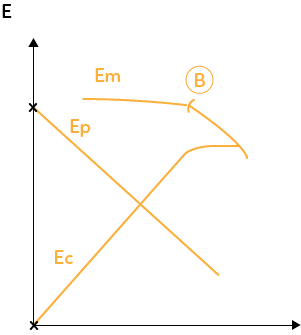
L’énergie cinétique croit plus doucement jusqu’à devenir constante, lorsque la force de frottement s’égale au poids. Si les deux forces se compensent, la somme des forces extérieures devient nulle et d’après la deuxième loi de Newton, l’accélération est alors nulle : la vitesse est donc constante.
Étude énergétique d’un problème mécanique - Mouvement d’un pendule
Le mouvement d’un pendule
Quelles sont les forces qui agissent sur un pendule ?
On étudie dans le référentiel terrestre les oscillations d’un pendule soumis à son poids (vertical vers le bas), à la tension du fil (dirigée du pendule vers le point de fixation du pendule) et les frottements de l’air (négligeables dans un premier temps).
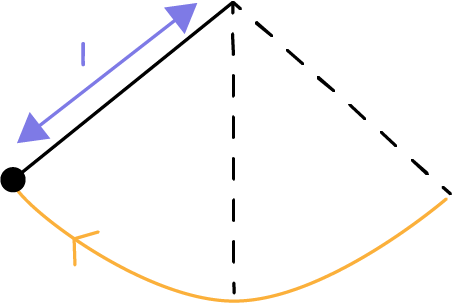
On considère les conditions initiales suivantes :
à $t = 0, \left \{ \begin{array}{c}
v_0 = 0 \text{ m.s}^{-1} \\
y_0 = h_0 \\
\end{array}
\right.$ où $h_0$ est la hauteur par rapport à la position verticale du pendule.
Quelles sont les deux énergies liées au mouvement d’un pendule ?
Les deux énergies liées à ce problème sont l’énergie cinétique : $E_c = \dfrac{1}{2} m v^2$, et l’énergie potentielle de pesanteur, liée au travail du poids entre $A$ et $B$, $E_p = mgh$.
En outre, la somme des deux est égale à l’énergie mécanique $E_m$.
Avant le lâcher sans vitesse initiale du pendule, la hauteur est maximale puis elle diminue au cours du temps jusqu’à atteindre la position au repos du pendule où elle est minimale (position verticale du pendule), puis le pendule remonte pour retrouver sa hauteur maximale : l’énergie potentielle de pesanteur suit la même évolution.
Au début, l’énergie cinétique est nulle puis lors de sa chute, le pendule gagne de la vitesse pour atteindre lorsque le pendule est vertical (sa position de repos) sa vitesse maximale et donc son énergie maximale, puis le pendule prend à nouveau de l’altitude et perd donc de la vitesse jusqu’à ce qu’elle redevienne nulle.
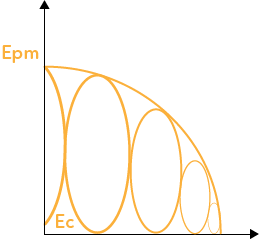
La somme des deux énergies est une constante, le poids étant une force conservative.
En prenant en compte les frottements de l’air, l’énergie mécanique diminue : le pendule oscille de moins en moins jusqu’à ce qu’il s’immobile totalement.
Comment est calculée la période d’oscillation d’un pendule ?
La période d’oscillation du pendule correspond à la durée nécessaire pour faire un aller-retour et est donnée par la formule $T = 2\pi \sqrt{\dfrac{l}{g}}$, où $l$ est la longueur du fil du pendule et $g$ l’intensité de pesanteur.


