Modèle ondulatoire et particulaire de la lumière
Modèle ondulatoire et particulaire de la lumière
I. Modèle ondulatoire
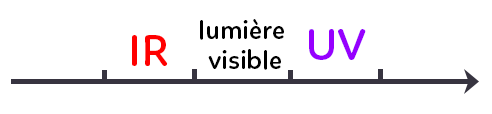
Dans ce modèle, la lumière est une onde, elle peut se réfléchir, se transmettre. La lumière visible est une onde électromagnétique, mais une partie seulement du spectre des ondes électromagnétiques.
Une onde est caractérisée par sa fréquence $f$ (en Hz) ou sa longueur d’onde $\lambda$ (en m). Une formule relie ces deux grandeurs :
$f=\dfrac{c}{\lambda}$ où $c$ est la célérité de la lumière et vaut $c =3 \times 10^8 \ m.s^{-1}$.
Exemples :
Pour $\lambda = 400 \ nm$ (bleu violet) on a $f=7,5 \times 10^{14}\ Hz$
Pour $\lambda = 800 \ nm$ (rouge) on a $f=3,8\times 10^{14}\ Hz$
La fréquence et la longueur d’onde sont inverses l’une de l’autre : quand $f$ est grand, $\lambda$ est petit et inversement.
II. Aspect particulaire
Dans ce modèle la lumière est un ensemble de photons. Chaque photon possède une énergie qui vaut $E_{photon}= h \times f = h \times \dfrac{c}{\lambda}$.
$h$ est la constante de Planck et vaut $h=6,63 \times 10^{-34}\ J.s$
Application numérique :
Pour $\lambda = 400\ nm$ on a $E_{photon,\ 400 \ nm}= 6,63 \times 10^{34} \times \dfrac{3,0 \times 10^8}{400 \times 10^{-9}}=4,97 \times 10^{-19}\ J$
L’électron-volt
On peut convertir les Joules en électron-volt, c’est une unité énergétique :
$1 \ eV = 1,6 \times 10^{-19} \ J$
Ainsi on a, $E_{photon,400 \ nm}=3,1 \ eV$ ce qui est plus agréable à manipuler.
Émission, absorption par l'atome
Émission, absorption par l’atome
I. Diagramme d’énergie d’un atome
Le diagramme d’énergie d’un atome est l’outil nécessaire aux calculs d’émission et d’absorption.
Un diagramme d’énergie sert à décrire les différents niveaux d’énergie possibles de l’atome. Ces niveaux sont quantifiés, ce qui signifie que les valeurs prises par les différents niveaux d’énergie sont discrètes et fixes. Ainsi, un atome ne peux qu’être aux niveaux d’énergie indiqués par le diagramme, mais jamais entre ces niveaux.
Le niveau le plus bas est le plus stable de tous. On l’appelle le niveau fondamental et on le note $E_1$. Viennent ensuite les niveaux $E_2$, $E_3$ et ainsi de suite. Ainsi, un niveau d’ordre $n$ est noté $E_n$. De la même manière, le dernier niveau est le niveau $E_\infty$, et sa valeur en énergie est de $0 \ eV$ (donc 0 J). On en déduit que tous les niveaux d’énergie inférieurs sont donc à des valeurs d’énergie négatives. Ces énergies sont des énergies dites potentielles (qui n’ont donc rien à voir avec l’énergie cinétique liée au mouvement de l’atome par exemple) qui correspondent à des énergies d’interaction entre le noyau et les électrons.
Déterminer les niveaux d’énergie d’un atome est un exercice complexe qui n’est pas au programme, le diagramme sera donc toujours fourni. Il existe pourtant des modèles permettant de déterminer les valeurs des niveaux d’énergie pour des cas simples tels que les atomes hydrogénoïdes (atomes composés d’un unique électron). Dans ce cas simple, la modélisation et le calcul des énergies d’interaction entre le noyau et l’électron est plus simple et on a donc accès au diagramme.
Le chiffre correspondant aux niveaux d’énergie est appelé nombre quantique principal $n.$ Il permet de repérer les niveaux d’énergie de l’atome. On a donc:
$n=1$ : Niveau fondamental, qui correspond à l’état le plus stable. Les électrons qui peuplent l’atome veulent donc se trouver à l’état fondamental car ils recherchent la stabilité.
$n>1$ : Si un électron peuple un niveau d’énergie supérieur à 1, on dit que l’atome est excité.
$n\rightarrow \infty$ : On parle d’état ionisé. Un modèle permettant de se représenter les états d’énergie (et donc de comprendre l’état ionisé) est de considérer un atome composé d’un noyau et d’un électron. L’électron décrit une trajectoire circulaire autour du noyau, à une distance finie. Il est dans l’état fondamental $E_1$, donc sur la couche $K.$ En lui fournissant de l’énergie, il passe sur l’orbite suivante plus éloignée, il est donc sur un autre niveau d’énergie appelé $E_2$. Ainsi, changer de niveau c’est changer d’orbite. En l’envoyant à une orbite infinie, on en conclut que l’électron est infiniment loin du noyau, il a été expulsé. On parle donc d’état ionisé car l’atome sans son électron est devenu un ion.
II. Absorption d’un photon
On considère un diagramme d’énergie à deux niveaux $E_1$ et $E_2$.
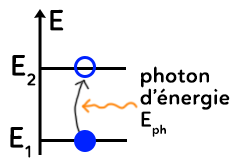
L’électron est initialement sur l’état fondamental. L’arrivée d’un photon d’énergie $E_{ph}$ sur l’atome peut permettre de faire passer l’électron du niveau d’énergie $E_1$ au niveau $E_2$ à condition que l’énergie du photon $E_{ph}$ soit précisément égale à l’énergie nécessaire pour passer du niveau 1 au 2.
Ainsi, si $E_{ph}=E_2-E_1=E_f-E_i=\Delta E$, il y a absorption : l’énergie du photon a été transférée à l’atome.
Rappels
Pour calculer l’énergie d’un photon, on sait que: $E_{ph}=h\times f=h\times\dfrac{c}{\lambda}$
$h$ : constante de Planck
$f$ : fréquence du photon
$c$ : célérité de la lumière ($c=3.10^8 \ m.s^{-1}$)
$\lambda$ : longueur d’onde du photon
III. Émission d’un photon
L’émission d’un photon correspond en quelque sorte au phénomène opposé de l’absorption.
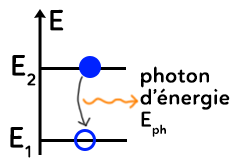
Pour un atome excité à la base, l’électron sera par exemple sur le niveau $E_2.$ Après un certain temps, l’atome va se désexciter pour retomber à son état fondamental, le niveau $E_1.$ En passant du niveau $E_2$ au niveau $E_1,$ l’atome perd nécessairement de l’énergie qui sera expulsée sous forme de photon. Ainsi, en se désexcitant, l’atome libère la différence d’énergie entre les deux états. L’énergie du photon, qui correspond à l’énergie libérée est donc égale à :
$E_{ph}=E_2-E_1=E_i-E_f=-\Delta E$
Remarque
On sait que $E_{ph}=h\times\dfrac{c}{\lambda}$
Ainsi, en connaissant l’état initial et final d’une émission, on peut donc retrouver la longueur d’onde du photon émis !