Roches et zones de subduction
Ce cours a pour but d’exposer l’intérêt de la microscopie optique dans la compréhension de la production de croûte continentale dans les zones de subduction.
En séance de travaux pratiques, il est de coutume d’étudier soit :
– des roches magmatiques plutoniques comme par exemple la diorite ou le granite qui ont des cristaux jointifs (juxtaposés sans espaces vides entre eux, du fait d’un refroidissement lent en profondeur), comme dans la photographie ci-dessous.

– des roches magmatiques volcaniques comme par exemple l’andésite ou la rhyolite.
La diorite (roche plutonique) a exactement la même composition minéralogique que l’andésite (roche volcanique). Le granite (roche plutonique) a la même composition minéralogique que la rhyolite (roche volcanique).
Les roches au niveau des zones de subduction, qu’elles soient volcaniques (rhyolite, andésite) ou plutoniques (diorite, granite), ont une spécificité : elles sont très riches en minéraux hydratés.
Ces minéraux sont observables en lames minces : ce sont par exemple les amphiboles (de type hornblende) ou le mica noir, qui sont riches en eau. La photographie ci-dessous d’un échantillon d’une roche magmatique en lumière polarisée analysée (LPA) montre ainsi un mica noir (en haut).

Puisqu’on sait que ces roches sont magmatiques, on peut donc en déduire que le magma qui leur a donné naissance était riche en eau.
D’où vient l’eau de ce magma ?
Elle est apportée par la plaque plongeante, en bleu dans le schéma ci-dessous, qui par le biais de réactions métamorphiques dues à l’augmentation de pression en profondeur (dans un domaine de stabilité dit de type faciès éclogite au schiste bleu), libère de l’eau.
Ces réactions métamorphiques hydratent ainsi le manteau de la plaque chevauchante, composé de péridotites (en vert sur le schéma). Par conséquent, le point de fusion du manteau de la plaque chevauchante diminue.
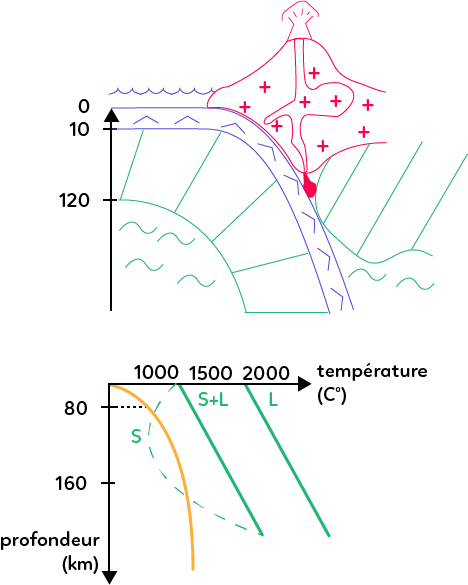
La courbe de solidus de la péridotite, en pointillés sur le schéma ci-dessus, est ainsi modifiée, et la température de fusion est abaissée.
Cette diminution de la température de fusion de la péridotite (composée essentiellement de pyroxènes et d’olivines) permet une fusion partielle (entre 80 et 160 kilomètres de profondeur) donnant naissance à un magma hydraté qui donne à son tour des roches magmatiques hydratées avec des minéraux hydratés que sont les amphiboles hydratées et les micas noirs hydratés.
Comment créer de la croute continentale ?
On estime actuellement que la croissance de la lithosphère continentale ou de la croûte continentale est presque nulle. La création de croûte continentale est compensée par sa destruction.
Les plus anciennes roches de croûte continentale ont 4 giga années (milliards d’années) : il s’agit des gneiss d’Acasta. Les deux tiers voire les trois quarts du volume de la croûte continentale ont été créés il y a très longtemps, à la fin de l’Archéen, il y a à peu près 2,5 giga années. On estime donc que le petit volume de croûte continentale créée est compensé par sa destruction.
Néanmoins, il y a bien création de croûte continentale, par notamment deux mécanismes.
I. La subduction
Le passage de la lithosphère océanique sous la plaque chevauchante induit un métamorphisme de moyenne et haute pression qui libère de l’eau.
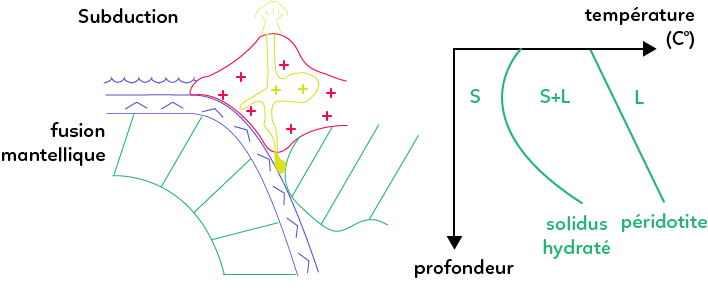
Cette eau vient hydrater une partie du manteau de la plaque chevauchante, et ainsi abaisser la température de fusion de la péridotite en modifiant son solidus.
Ce processus crée ainsi une fusion partielle de la péridotite mantellique produisant un magma. Une partie cristallise lentement en profondeur donnant de la diorite mais également rapidement en surface donnant de l’andésite.
L’andésite et la diorite sont donc les roches caractéristiques de la croûte continentale formées au niveau des zones de subduction par fusion partielle du manteau.
II. La collision
Lorsqu’il y a un mouvement de convergence avec des forces compressives importantes, il y a création de croûte continentale par anatexie crustale (ou épaississement crustal). L’anatexie crustale est la conséquence d’un métamorphisme poussé à l’extrême.
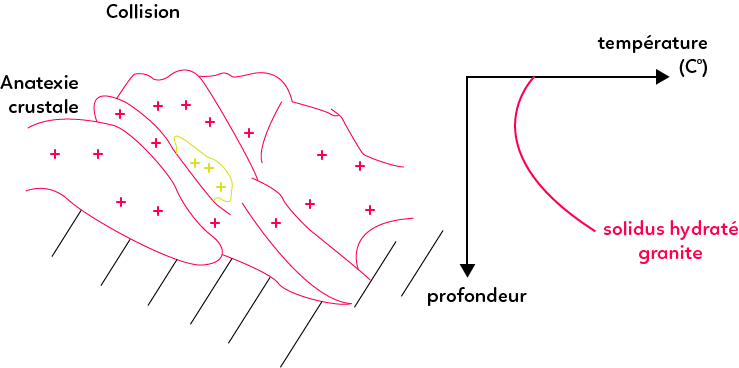
En effet, lorsque deux lithosphères continentales se rencontrent (collision), des pans entiers de croûte continentale se chevauchent : ce sont les nappes de charriage, en rouge dans le schéma ci-dessous.
Cette croûte continentale est alors chaude et réchauffe les zones en profondeur. L’augmentation de température induite permet alors le passage du solidus hydraté du granite et donc une fusion partielle de la roche et l’apparition d’un magma.
Le magma va ensuite se refroidir et cristalliser au sein de la croûte continentale, en jaune sur le schéma de la collision ci-dessus. Il y a donc ainsi également création de croûte continentale.
La distribution des foyers sismiques dans les zones de subduction
I. L’archipel des Mariannes
Un exemple de distribution des foyers sismiques en zone de subduction : l’archipel des Mariannes, avec sa fosse éponyme.

Comme on le voit sur ces images, l’archipel des Mariannes est un chapelet d’îles ayant une forme d’arc. On parle d’arc insulaire. En zoomant sur cette localisation, on observe très clairement cette bathymétrie avec une fosse très profonde : la fosse des Mariannes.
La bathymétrie est la science qui étudie le relief sous-marin afin de déterminer sa topographie.

Avec le logiciel Sismolog, il est possible de voir une vision 3D de la région. On voit ainsi très nettement le chapelet d’îles, contenant de nombreux volcans disposés parallèlement à la fosse. On retrouve aussi dans cette vue 3D la disposition des foyers sismiques. Ils sont eux aussi parallèles à la fosse.
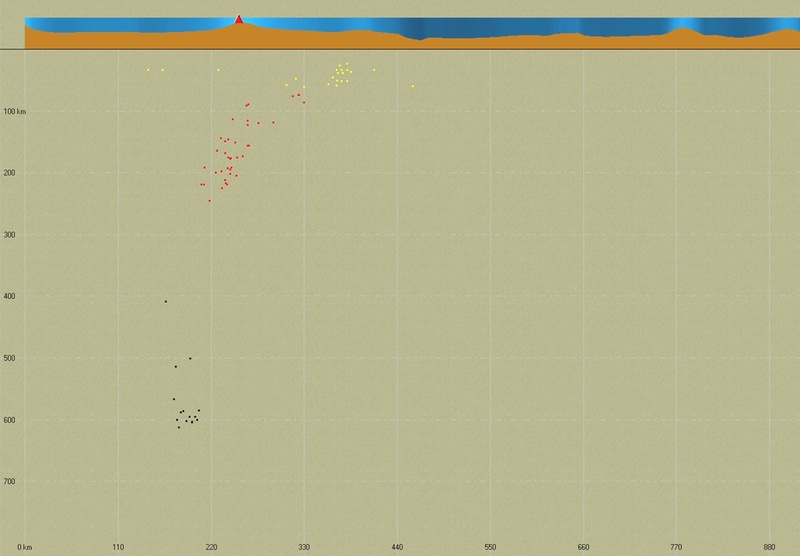
Lorsque l’on fait une coupe transversale, perpendiculaire à l’alignement des volcans, on observe que les foyers sismiques des séismes sont distribués selon une ligne, qui en 3D donnerait un plan. Ce plan est appelé plan de Wadati-Benioff.
II. Schématisation d’une coupe
Schématisons ce que nous avons appris grâce au logiciel Sismolog sous forme d’une coupe transversale.
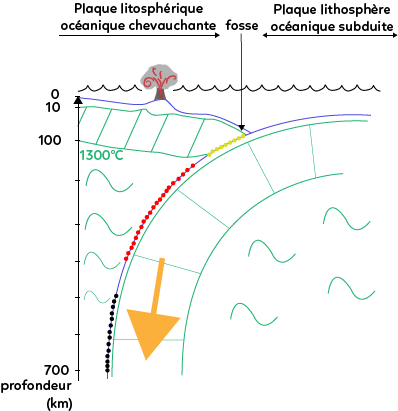
On a vu que les foyers sismiques s’alignent sur un plan, et que les séismes peuvent atteindre jusqu’à 700 km de profondeur. Le repère de profondeur partira donc de 0, pour atteindre -700 km.
On va ensuite tracer une plaque avec un fort angle de pendage qui va donc « plonger ». Cette plaque est formée de croûte océanique ainsi que d’un manteau lithosphérique très épais. L’ensemble de la plaque est donc très dense, ce pourquoi elle peut plonger dans l’asthénosphère. La plaque plongeante est représentée en vert, car elle est essentiellement composée de péridotite.
Les séismes superficiels sont représentés en jaune, ceux de profondeur moyenne en rouge, et ceux de forte profondeur (autour de 700 km) en noir.
La plaque lithosphérique plonge dans l’asthénosphère. En face de cette plaque plongeante, une autre plaque appelée plaque chevauchante est présente, elle-même composée de croûte et de manteau lithosphérique. À la surface de cette deuxième plaque, on observe un volcanisme actif. Certains de ces volcans émergent au-dessus du niveau de la mer.
Il est essentiel de comprendre qu’en temps normal, il ne peut pas y avoir de séismes au-delà de 100 km de profondeur. En effet, un séisme correspond à une cassure brutale de la roche. À partir de 100 km, cette cassure n’est plus possible car l’isotherme 1 300°C est atteint, c’est-à-dire la limite entre la roche rigide et ductile. Alors, comment expliquer la présence de séismes à des profondeurs de 700 km ?
On explique cela par le plongement d’un matériau rigide et donc cassant (la lithosphère). Ce plongement s’explique par la forte densité de la lithosphère, bien plus dense que celle du manteau sous-jacent. La densité de la lithosphère est ainsi le moteur de la subduction.
Bilan
La distribution des foyers sismiques en zone de subduction se fait selon le plan de Wadati-Benioff. Cette distribution particulière met en évidence l’existence d’une lithosphère cassante, rigide, plongeant dans l’asthénosphère ductile au sein de l’archipel des Mariannes. Ce plongement est également visible de par la fosse des Mariannes qui délimite la plaque lithosphérique chevauchant de la plaque subduite.


