Symétrie centrale
Symétrie centrale
1) Aspect visuel
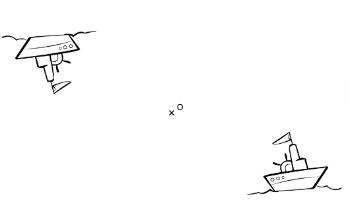
Visuellement, l’image par symétrie centrale d’une figure par rapport à un point correspond à un demi tour de 180° de la figure par rapport au point.
2) Symétrique par rapport à un point
On donne ici une définition mathématique de la symétrie centrale.
On dit que $A’$ est le symétrique de $A$ par rapport à $O$ lorsque $O$ est le milieu de $[AA’]$.
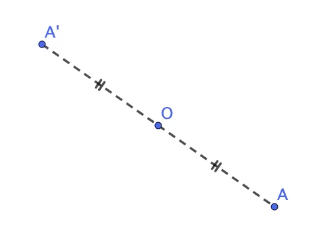
Pour obtenir le symétrique du point $A$ par rapport à $O$, on trace le segment reliant $A$ à $O$ puis on reporte la longueur $AO$ sur la demi droite $[AO)$. Le point $A’$ situé à la distance $AO$ de $O$ est appelé symétrique de $A$ par rapport à $O$.
3) Symétrique d’un segment
Pour construire le symétrique d’un segment $[AB]$ par rapport à $O$, on applique la même méthode que précédemment en construisant successivement le symétrique $A’$ de $A$ par rapport à $O$ puis le symétrique $B’$ de $B$ par rapport à $O$.
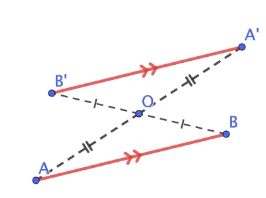
On remarque alors que $AB = A’B’$. On dit alors que la symétrie centrale conserve les longueurs.
En outre, les droites $(AB)$ et $(A’B’)$ sont parallèles.
4) Symétrique d’une figure
Pour obtenir le symétrique d’un polygone par rapport à un point $O$, on construit le symétrique de tous les points du polygone par rapport à $O$ puis on relie l’ensemble de ces points entre eux pour former le symétrique.
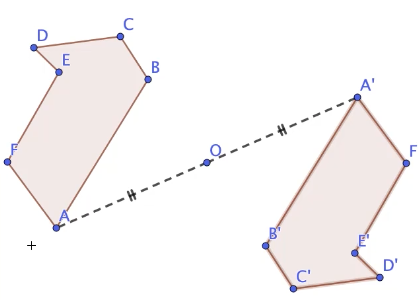
Le symétrique ainsi obtenu a la même aire que la figure initiale.
En outre, les deux figures ne sont pas superposables.
Centre de symétrie
Centre de symétrie
1) Définition
Une figure admet un centre de symétrie si, lorsqu’on la fait tourner d’un demi-tour autour de ce point, elle ne varie pas.
Il ne faut pas confondre centre de symétrie qui fait référence à la symétrie centrale et axe de symétrie en lien avec la symétrie axiale.
Exemple :
La carte de 10 de pique admet un centre de symétrie $O$ car lorsqu’on la fait tourner d’un demi-tour autour de ce point, la figure obtenue est identique à celle de départ.

2) Centres de symétrie de figures usuelles
On s’intéresse aux figures souvent rencontrées en géométrie.
Le parallélogramme, le rectangle, le losange et le carré admettent un centre de symétrie. De même, l’hexagone régulier admet un centre de symétrie.
A l’inverse, un trapèze n’admet pas de centre de symétrie car en faisant tourner ce quadrilatère autour d’un point, la figure obtenue est différente de la figure initiale.
3) Autres figures
On s’intéresse ici aux figures rencontrées dans le code de la route. Il est important de noter que l’on peut chercher un éventuel centre de symétrie à chaque figure géométrique plane.
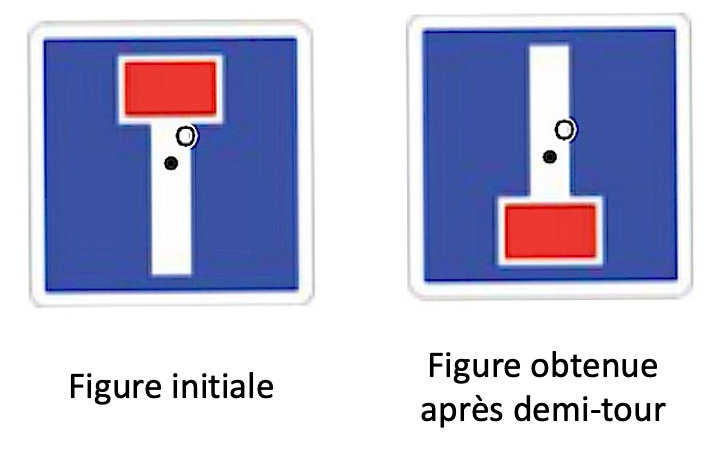
Le panneau “impasse” n’admet pas de centre de symétrie car après rotation, la figure obtenue est différente.
Le panneau indiquant la présence d’un hôpital admet un centre de symétrie.
Le panneau indiquant une interdiction de demi-tour ne présente pas de centre de symétrie.



