Équation quotient
Équation quotient nul
Définition
Une équation quotient nul est une équation du type $\dfrac{A(x)}{B(x)}=0$ avec $B(x)\neq 0$
On cherche si elles existent, la ou les valeurs de $x$ qui vérifient cette équation.
On rappelle qu’un quotient est nul si et seulement si le numérateur est nul.
Exemple
Considérons l’équation quotient suivante : $\dfrac{2x + 1}{3x – 1} = 0$.
Ici, le dénominateur est inconnu dans la mesure où il fait intervenir la variable $x$ que l’on cherche à déterminer.
La première étape consiste à trouver les valeurs interdites, c’est à dire les valeurs que la variable $x$ ne doit pas prendre car diviser par 0 est impossible.
Il faut donc veiller à ce que le dénominateur ne soit jamais nul.
Ainsi, pour trouver ces valeurs qui ne conviennent pas, on résout l’équation $3x – 1 = 0$ c’est à dire $x = \dfrac{1}{3}$.
La résolution de l’équation commence alors en énonçant les valeurs de $x$ possibles.
Ainsi, pour tout $x \in \mathbb{R} \backslash \left\{\dfrac{1}{3}\right \}$, on a $\dfrac{2x + 1}{3x – 1} = 0$.
Ce quotient est nul si et seulement si le numérateur est nul.
Ainsi, $2x + 1 = 0$ c’est à dire $x = -\dfrac{1}{2}$. Il faudra veiller à ce que la solution trouvée ne soit pas aussi une valeur interdite.
Ainsi, $S = \left\{ -\dfrac{1}{2} \right \}$.
Autre exemple
Considérons de même l’équation quotient suivante : $\dfrac{4x -3}{2x + 6} = 0$.
On cherche la valeur interdite : $2x + 6 = 0$ c’est à dire $x = -3$.
Ainsi, pour tout $x \in \mathbb{R} \backslash \{-3 \}$, on a $\dfrac{4x -3}{2x + 6} = 0$.
Or un quotient est nul si et seulement is le numérateur est nul.
Ainsi $4x – 3 = 0$ c’est à dire $x = \dfrac{3}{4}$.
La solution n’étant pas une valeur interdite, $S = \left \{ \dfrac{3}{4} \right \}$
Inéquations produit, tableau de signes
Inéquations produit
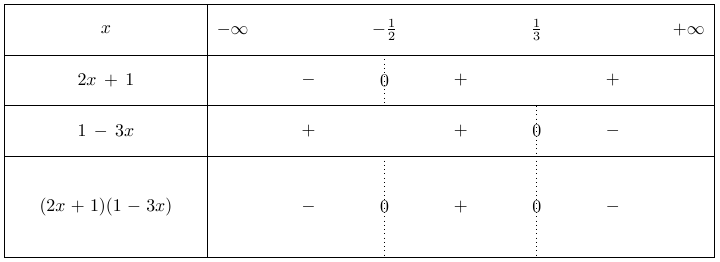
On souhaite résoudre l’inéquation suivante $(2x + 1)(1 – 3x) \geq 0$.
Il est bon de s’interroger sur l’existence d’une solution.
Si le premier facteur est positif, ainsi que le second, alors par produit, le résultat est positif.
De même, si le premier facteur est négatif, ainsi que le second, alors par produit, le résultat est positif.
Néanmoins, si les deux facteurs n’ont pas le même signe, il n’existe pas de solution.
On étudie donc le signe de chaque facteur en fonction de $x$.
On cherche donc tout d’abord pour quels $x$ le facteur $2x + 1$ est positif ou nul, ou encore, on veut résoudre $2x + 1 \geq 0$.
Cela revient à écrire que $2x \geq -1$ ou encore $x \geq \dfrac{-1}{2}$. Ainsi, si $x \geq \dfrac{-1}{2}$, on a $2x + 1 \geq 0$.
De même, on veut résoudre $1 – 3x \geq 0$, c’est à dire $-3x \geq -1$ soit $x \leq \dfrac{1}{3}$ (il faudra prêter attention au fait que multiplier ou diviser par un nombre négatif change le sens de l’inégalité).
On reporte ensuite les informations trouvées précédemment dans un tableau de signe.
On indique dans la première ligne les valeurs de $x$ classées par ordre croissant, c’est à dire les valeurs calculées.
En dessous des valeurs $\dfrac{-1}{2}$ et $ \dfrac{1}{3}$, on trace un trait vertical.
La deuxième ligne contient le signe de $2x + 1$ sur les différents intervalles.
En reprenant le premier calcul, on a montré que $2x + 1$ était positif si $x \geq \dfrac{-1}{2}$ : on indique donc les cases à droite de $\dfrac{-1}{2}$ un signe $+$ pour indique que la positivité du nombre pour les valeurs de $x$ considérées.
Il reste ensuite à écrire un signe $-$ dans la case non remplie pour signifier que $2x + 1$ est négatif ici.
Enfin, sur le trait correspondant (c’est à dire celui associé à $x = \dfrac{-1}{2}$, on indique un $0$ pour signifier la nullité de l’expression.
La troisième ligne indique le signe de $1 – 3x$.
Pour la remplir, on utilise le calcul trouvant à quelles conditions $1 – 3x$ est positif : on avait alors trouvé que cela se réalisait pour $x \leq \dfrac{1}{3}$, c’est à dire des nombres plus petits que $\dfrac{1}{3}$.
On écrit donc des signes $+$ dans les cases à gauche de $dfrac{1}{3}$.
Enfin, pour remplir la dernière ligne, qui donne le signe du produit en utilisant la règle des signes pour les produits.
Pour répondre à notre question initiale, à savoir résoudre l’inéquation $(2x + 1)(1 – 3x) \geq 0$, on utilise le tableau de signe en gardant uniquement les intervalles pour lesquelles le signe est un $+$, c’est à dire
$S = \left [\dfrac{-1}{2}; \dfrac{1}{3} \right ]$.
Inéquations quotients
Inéquations quotients
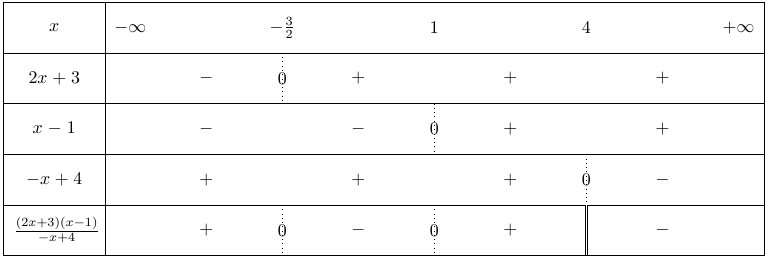
On souhaite résoudre l’inéquation quotient suivante : $\dfrac{(2x + 3)(x -1)}{-x + 4} < 0$.
La première étape consiste, lorsque l’inconnue apparait au dénominateur, à chercher les valeurs de $x$ pour lesquelles le dénominateur s’annule, même si ce n’est pas clairement indiqué dans l’énoncé.
On cherche donc $x$ tel que $-x + 4 = 0$ c’est à dire $x = 4$. La valeur interdite est donc le nombre 4.
On présente donc ensuite l’intervalle d’étude de l’inéquation.
Pour tout $x \in \mathbb{R} – \{4\}$, étudions les signes de chaque terme séparément.
$2x + 3 \geq 0 \iff 2x \geq -3 \iff x \geq \dfrac{-3}{2}$
$x – 1 \geq 0 \iff x \geq 1 $
$-x + 4 \geq 0 \iff -x \geq – 4 \iff x \leq 4$ car multiplier ou diviser par un nombre négatif change le sens de l’inégalité.
On complète à présent le tableau de signe.
On écrit dans la première ligne du tableau les valeurs de $x$ particulières que l’on a trouvé précédemment, en les classant par ordre croissant.
On trace ensuite en dessous de ces valeurs un trait verticale.
Enfin, on trace une double valeur verticale en dessous de $x = 4$ sur la ligne du quotient pour indiquer que $x = 4$ est une valeur interdite.
On peut désormais remplir les autres cases du tableau, en indiquant par un $+$ ou un $-$ le signe des expressions sur les intervalles considérés.
Par exemple $2x + 3 \geq 0$ si $x \geq \dfrac{-3}{2}$, on marque donc un $+$ à droite de $x = \dfrac{-3}{2}$ puis un $-$ de l’autre côté, en indiquant enfin un $0$ sur le trait vertical sous $x = \dfrac{-3}{2}$.
On remplit de même les deux lignes suivantes, à l’aide des calculs faits précédemment.
Pour remplir la dernière ligne contenant les informations du signe du quotient, on utilise la règle des signes.
Enfin, il faut encore résoudre l’inéquation : on cherchait les $x$ tels que le quotient soit négatif, on ne garde donc que les intervalles sur lesquels le quotient est de signe $-$.
On prendra garde à ne pas considérer les valeurs de $x$ pour lesquelles le quotient s’annule car l’inéquation utilise une inégalité stricte.
Ainsi, $S = \left ] -\dfrac{3}{2}; 1 \right [ \cup ]4; + \infty [$.
Équation produit nul
Équation produit nul
Définition
Une équation produit nul est une équation s’écrivant sous la forme d’un produit dont le résultat est nul.
Exemple
Considérons par exemple l’équation :
$x(x^2 – 9)(1 – x) = 0$
Pour résoudre cette équation, il ne faut pas développer. Il faut factoriser l’expression, et en particulier le terme $x^2 – 9$ :
On reconnait une identité remarquable et on réécrit ainsi ce terme sous la forme $(x – 3)(x + 3)$.
L’équation dévient :
$x(x – 3)(x + 3)(1 – x) = 0$.
Or un produit est nul si au moins l’un de ces facteurs est nul.
L’équation s’écrit alors :
$x = 0$ OU $x – 3 = 0$ OU $x + 3 = 0$ OU $1 -x = 0$
On résout alors séparément chacune de ces équations.
$x = 0$ OU $x = 3 $ OU $x = -3$ OU $x = 1$
Les solutions sont donc $S = \{-3; 0; 1; 3\}$.