Formules des probabilités
Formules des probabilités
Définition
Soient $A$ et $B$ deux événements de $\Omega$, l’ensemble des issues d’une expérience aléatoire.
La probabilité d’un événement $P(A)$ se calcule grâce au quotient suivant :
$P(A) = \dfrac{\text{nombre d’éléments de } A}{\text{nombre d’issues de } \Omega}$.
En outre, une probabilité est toujours comprise entre 0 et 1 (le nombre d’issues de $A$ ne peut être négatif et il ne peut pas dépasser le nombre d’éléments de $\Omega$).
Propriétés
La probabilité de l’ensemble vide vaut 0 : $P(\varnothing) = 0$.
La probabilité de $\Omega$ vaut 1 : $P(\Omega) = 1$.
Par exemple, si on considère l’expérience du lancé de dé, l’univers $\Omega$ est l’ensemble des entiers compris entre 1 et 6, donc
$P(\Omega) = \dfrac{\text{nombre d’issues de } A}{\text{nombre d’issues de } \Omega} = \dfrac{6}{6} = 1$.
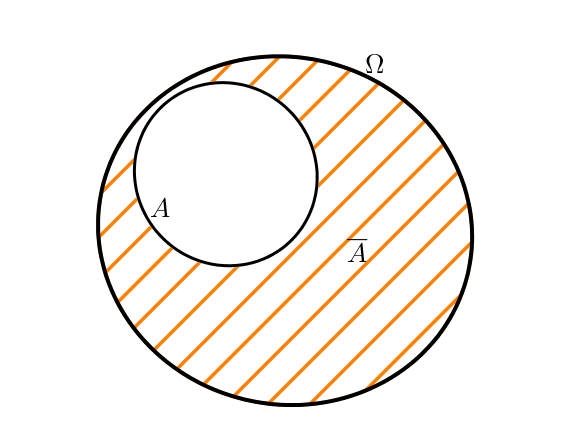
Événement contraire
La probabilité de l’événement contraire à $A$, noté $\overline{A}$ et contenant toutes les issues n’appartenant pas à $A$, vaut
$P(\overline{A}) = 1 – P(A)$.
Probabilité de la réunion de deux événements
Pour calculer la probabilité de la réunion de deux événements, il est possible de compter le nombre d’issues appartenant à la réunion mais il existe aussi une formule :
$P(A \cup B) = P(A) + P(B) – P(A \cap B)$.
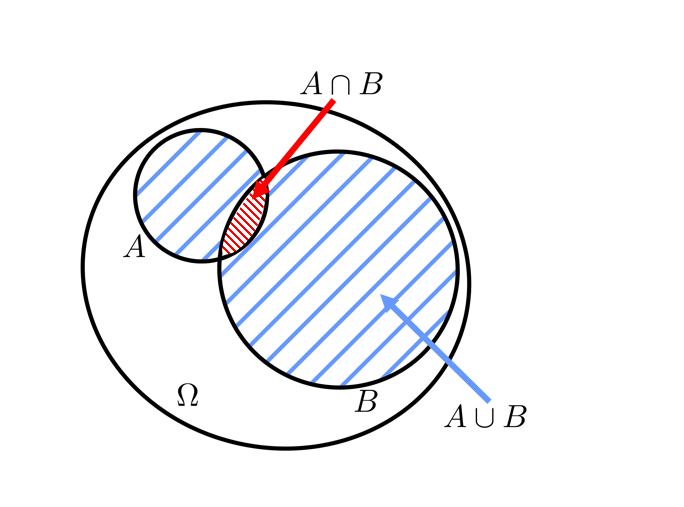
Cette formule dit que la probabilité de la réunion est égale à la somme des probabilités des deux événements à laquelle on soustrait la probabilité de l’intersection car on avait compté deux fois les issues appartenant à la fois à $A$ et à la fois à $B$ (on les avait ajoutées lors du calcul de $P(A)$ puis on les avait ajoutées à nouveau pour le calcul de $P(B)$).
Exemple :
On lance un dé à 6 faces.
On considère les événements
$A = “\text{obtenir un nombre pair}”$
$B = \text{“obtenir un nombre plus grand que 5”}$.
On cherche à calculer $P(A\cup B)$ :
$P(A\cup B) = P(A) + P(B) – P(A \cap B)$.
Or il y a trois nombres pairs possibles (2; 4; 6), donc $P(A) = \dfrac{3}{6} = \dfrac{1}{2}$.
Et il y a deux nombres plus grands que 5 ainsi $P(B) = \dfrac{2}{6} = \dfrac{1}{3}$.
Aussi, il existe un nombre pair et plus grand que 5 (c’est le nombre 6), donc $P(A \cap B) = \dfrac{1}{6}$.
Ainsi, $P(A\cup B) = \dfrac{1}{2} + \dfrac{1}{3} – \dfrac{1}{6} = \dfrac{2}{3}$.
Il était également possible de compter directement les issues appartenant à $A \cup B = \{2; 4; 5; 6\}$.
Ainsi, $P(A\cup B) = \dfrac{4}{6} = \dfrac{2}{3}$
Intersection et réunion d'événements
Intersection et réunion d’événements
Pour introduire la notion d’intersection et de réunion, on considère un exemple.
On lance deux dés et on s’intéresse à la somme des points obtenus.
Les issues possibles, l’univers, sont $\Omega = \{2; 3; 4; 5; …; 12 \}$.
On définit l’événement $A$ qui est d’obtenir une somme paire :
$A = \{2; 4; 6; 8; 10; 12 \}$ et l’événement $B$ qui est d’obtenir une somme supérieure ou égale à 7 :
$B = \{7; 8; 9; 10; 11; 12 \}$.
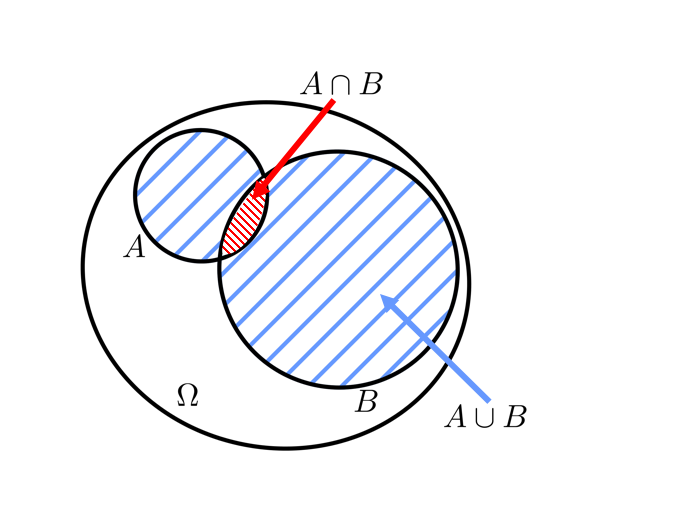
L’intersection
L’intersection de deux droites est le point appartenant à la fois à la droite $(d_1)$ et à la droite $(d_2)$.
L’intersection de deux événements, notée $A \cap B$ ($A$ inter $B$), correspond donc à toutes les issues communes aux événements $A$ et $B$.
Ici, $A \cap B = \{8; 10; 12 \}$.
La réunion
La réunion de deux événements, notée $A \cup B$ ($A$ union $B$), correspond à toutes les issues appartenant à $A$ ou à $B$.
Il faudra cependant éviter d’écrire deux fois les issues appartenant aux deux événements.
Ici, $A \cup B = \{2; 4; 6; 7; 8; 9; 10; 11; 12 \}$.
Vocabulaire des probabilités
Vocabulaire des probabilités
Afin d’introduire le vocabulaire lié aux probabilités, on considère l’exemple suivant :
On lance deux dés non truqués et on s’intéresse à la somme des points obtenus : il s’agit donc d’une expérience aléatoire dont on connait les résultats mais dont on ignore lequel se réalise.
L’ensemble des résultats possibles, c’est à dire toutes les issues possibles, s’appelle l’univers et est noté $\Omega$.
Ici, $\Omega = \{2; 3; 4; 5; …; 12\}$, c’est à dire tous les entiers compris entre 2 et 12.
Il est possible de définir un sous-ensemble de $\Omega$, appelé événement, comme par exemple l’événement $A$ qui est d’obtenir une somme paire :
$A = \{2; 4; 6; 8; 10; 12 \}$ ou encore l’événement $B$ qui est d’obtenir une somme égale à 10 :
$B = \{10 \}$.
$B$ est un événement élémentaire, c’est à dire qui ne contient qu’un seul résultat.
Un événement certain est un événement qui se réalise forcément : par exemple l’événement $\Omega$ est un événement certain : la somme est forcément comprise entre 2 et 12 quelque soit le résultat du lancé.
Un événement impossible est un événement qui ne peut pas se réaliser,
l’événement $C = \{13 \}$ est un événement impossible par exemple.
L’événement contraire à un événement $D$ est l’ensemble des issues appartenant à $\Omega$ mais qui n’appartiennent pas à $D$.
On note cet événement $\overline{D}$, qu’on lit “$D$ barre”.
Par exemple $\overline{A} = \text{“obtenir une somme impaire”} = \{3; 5; 7; 9; 11 \}$.


