Trigonométrie - Le rappel de cours
Trigonométrie – Le rappel de cours
Définition
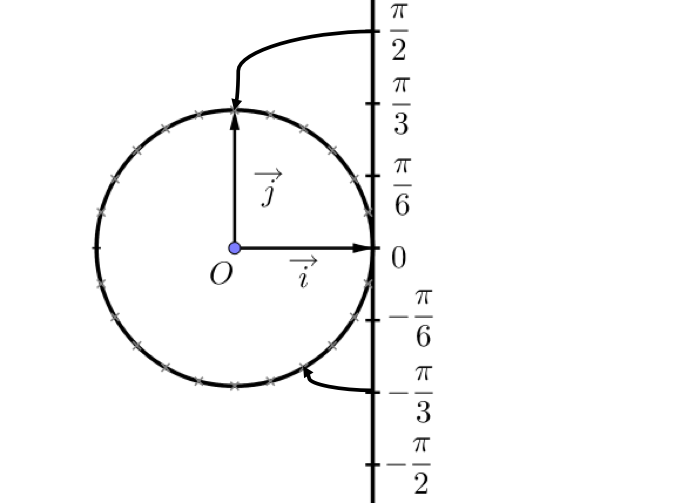
On considère un cercle de centre $O$ et de rayon 1, appelé cercle trigonométrique, ainsi qu’une droite numérique verticale variant de moins l’infini à plus l’infini et tangente au cercle au point de coordonnées $(1; 0)$.
Cette droite, à la manière d’une ficelle, peut s’enrouler autour du cercle.
Au bout d’un certain temps, la droite réalise un tour de cercle.
Or le rayon du cercle valant 1, le périmètre de ce dernier vaut donc $2 \pi \times 1 = 2 \pi$.
Ainsi, le point de la droite valant $2 \pi$ coïncide après enroulement avec le point de départ.
On définit ainsi une nouvelle mesure pour les angles, en plus que les degrés (variant de $0°$ à $360°$) : les radians.
En ayant effectué un tour de cercle, soit $360°$, cela correspondra à $2 \pi$ radians.
On peut alors remplir le tableau de correspondance suivant :
| Mesure en degrés | 0 | 30 | 45 | 60 | 90 | 180 | 360 |
| Mesure en radians | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{3}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ | $2 \pi$ |
La mesure en radians correspond donc à la longueur du segment enroulé autour du cercle.
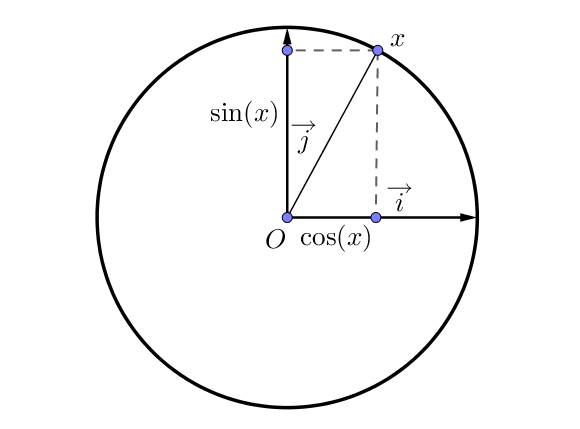
On place sur le cercle trigonométrique le nombre $x$.
Le cosinus de cet angle, noté $\cos(x)$ correspond à l’abscisse de ce point alors que le sinus, noté $\sin(x)$, correspond à l’ordonnée de ce point.
Trigonométrie - Les valeurs à connaître
Trigonométrie – Les valeurs à connaître
Pour rappel, le cosinus d’un angle correspond à l’abscisse du point sur le cercle associé et le sinus correspond à l’ordonnée du point.
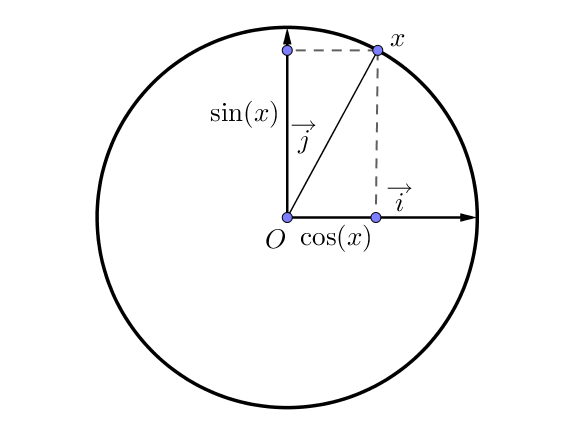
Lorsque l’angle vaut $0°$, on a $\cos(0) = 1$ et $\sin(0) = 0$.
Lorsque l’angle vaut $90°$ ou $\dfrac{\pi}{2}$ radians, on a $\cos(90) = 0$ et $\sin(90) = 1$.
Lorsque l’angle vaut $180°$ ou $\pi$ radians, on a $\cos(180) = -1$ et $\sin(180) = 0$.
Les mesures précédentes peuvent se retrouver par lecture graphique.
Lorsque l’angle vaut $45°$ ou $\dfrac{\pi}{4}$ radians, on a $\cos(45) = \dfrac{\sqrt{2}}{2}$ et $\sin(45) = \dfrac{\sqrt{2}}{2}$, qu’il faut retenir par coeur.
Dans ce cas, le cosinus et le sinus sont égaux: en effet, l’angle est situé sur l’axe de symétrie d’équation $y =x$.
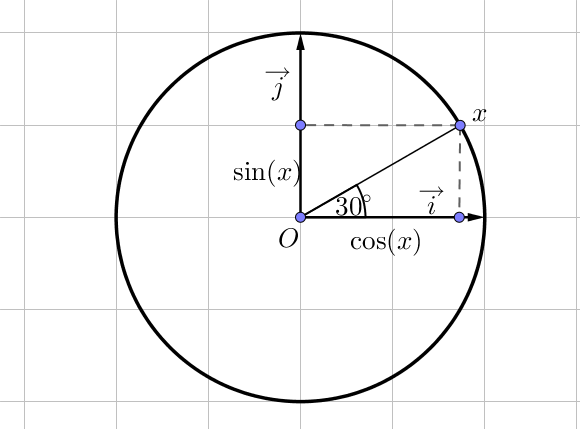
Graphiquement, on trouve que le sinus de l’angle $30°$ ou encore $\dfrac{\pi}{6}$ vaut $0,5$.
On en déduit alors que le cosinus vaut $\dfrac{\sqrt{3}}{2}$ (car $\cos(30)^2 + \sin(30)^2 = 1$).
De même, on trouve que le cosinus de l’angle $60°$ ou encore $\dfrac{\pi}{3}$ vaut $0,5$.
On en déduit alors que le sinus vaut $\dfrac{\sqrt{3}}{2}$.
On peut désormais rassembler ces informations dans le tableau suivant et on place sur les deux premières lignes du tableau les correspondances entre les mesures d’angles exprimées en degrés et en radians.
| Mesure en degrés | $0$ | $30$ | $45$ | $60$ | $90$ | $180$ |
| Mesure en radians | $0$ | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ |
| $\cos(x)$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ | $-1$ |
| $\sin(x)$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ | $0$ |