PGCD
À retenir :
Plus Grand Diviseur Commun à deux nombres.
Lorsqu’on a des petits nombres (exemple 18 et 27), on recherche les diviseurs des deux nombres.
Pour les nombres plus grands (exemple 168 et 70), on peut utiliser deux méthodes :
- Algorithme des différences (soustractions).
- Algorithme d’Euclide (divisions euclidiennes).
Simplification des expressions avec radical
Exemple :
- \( \sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3} = 4 \sqrt{3}\)
- \( \sqrt{75} = \sqrt{25 \times 3} = \sqrt{25} \times \sqrt{3} = 5 \sqrt{3}\)
- \( \sqrt{48} + \sqrt{75} = 4 \sqrt{3} + 5 \sqrt{3} = 9 \sqrt{3}\)
Angle inscrit - Angle au centre
Angles inscrits – Angles au centre
Définition
Un angle inscrit est un angle dans un cercle dont le sommet appartient au cercle et dont les côtés coupent le cercle en formant un arc de cercle appelé arc intercepté.
Un angle au centre est un angle dont le sommet est le centre du cercle et dont les côtés coupent le cercle.
Théorèmes
Dans un cercle, deux angles inscrits qui interceptent le même arc sont égaux.
Dans un cercle, l’angle inscrit mesure la moitié de l’angle au centre associé (qui intercepte le même arc).
Exemple :
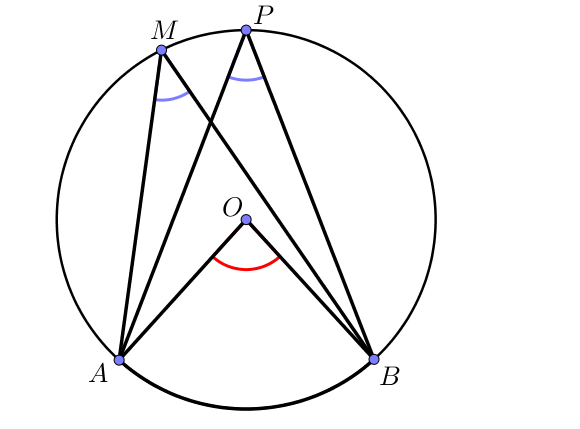
Supposons par exemple que $\widehat{AMB} = 20°$.
Il s’agit d’un angle inscrit interceptant l’arc $\overset{\frown}{AB}$.
L’angle $\widehat{APB}$ est aussi un angle inscrit qui intercepte le même arc, ainsi $\widehat{APB} = 20°$.
Enfin, l’angle $\widehat{AOB}$ est un angle au centre associé aux deux angles inscrits précédents, ainsi, $\widehat{AOB} = 40°$.
Quartiles
Quartiles
Lors du calcul de la médiane, il fallait découper la série statistique en deux sous séries de même longueur.
Pour le calcul des quartiles, il faut découper la série statistique en quart.
Définition :
Le premier quartile noté $Q_1$ correspond à la plus petite valeur telle que au moins un quart des termes de la série statistique ont une valeur inférieure ou égale à $Q_1$.
Le troisième quartile noté $Q_3$ correspond à la plus petite valeur telle que au moins trois quarts des termes de la série statistique ont une valeur inférieure ou égale à $Q_3$.
Exemple :
On considère la série statistique suivante représentant le poids de sept personnes. Déterminons les quartiles de cette série.
$ 65 \ ;\ 54\ ;\ 84\ ;\ 66\ ;\ 84\ ;\ 59\ ;\ 70$
Pour obtenir les deux quartiles à partir de cette série statistique, il faut d’abord la classer par ordre croissant.
$\ 54\ ;\ 59\ ;\ 65\ ;\ 66\ ;\ 70\ ;\ 84\ ;\ 84$
Pour déterminer le premier quartile, on commence par calculer le quart de l’effectif.
Ici, l’effectif est égal à 7 : $\dfrac{1}{4} \times 7 = 1,75$.
Cela signifierait alors que le premier quartile serait le terme de rang 1,75 qui n’existe pas.
Dans ce cas là, le premier quartile est le terme dont le rang est le premier entier supérieur au résultat du calcul précédent.
Ici, le premier quartile est donc le terme de rang 2, c’est à dire
$Q_1 = 59$ kg.
Pour déterminer le troisième quartile, on commence par calculer les trois quarts de l’effectif.
Ici, $\dfrac{3}{4} \times 7 = 5,25$.
Comme précédemment, le troisième quartile est le terme dont le rang est le premier entier supérieur au résultat du calcul précédent.
Ici, le troisième quartile est donc le terme de rang 6, c’est à dire
$Q_3 = 84$ kg.