Trigonométrie
Trigonométrie
La trigonométrie permet de mettre en relation des longueurs et des angles dans un triangle rectangle.
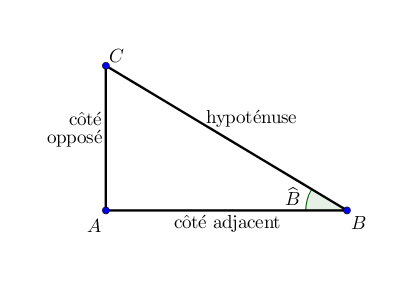
Vocabulaire
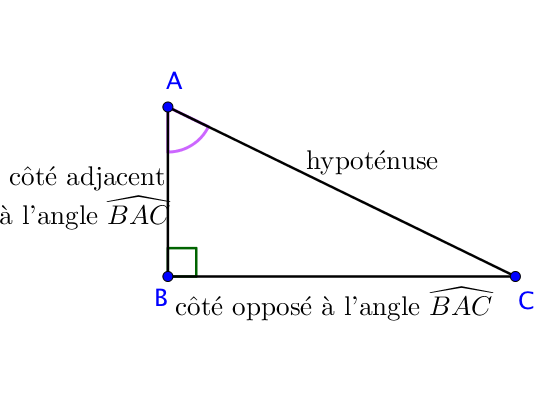
L’hypoténuse correspond au plus grand côté, en face de l’angle droit.
Le côté touchant l’angle $\widehat{B}$ autre que l’hypoténuse est appelé le côté adjacent.
Le côté en face de l’angle $\widehat{B}$ est appelé le côté opposé.
On définit ainsi le cosinus, le sinus et la tangente de l’angle $\widehat{B}$ par :
$\cos \widehat{B} = \dfrac{\text{côté adjacent}}{\text{hypoténuse}}$
$\sin \widehat{B} = \dfrac{\text{côté opposé}}{\text{hypoténuse}}$
$\tan \widehat{B} = \dfrac{\text{côté opposé}}{\text{côté adjacent}}$
Un moyen mnémotechnique pour se souvenir de ses définitions est :
CAH-SOH-TOA :
Cosinus = Adjacent divisé par l’Hypoténuse,
Sinus = Opposé divisé par l’Hypoténuse,
Tangente = Opposé divisé par Adjacent
Propriétés
Le cosinus et le sinus d’un angle sont reliés par la relation suivant : $(\cos \widehat{B})^2 + (\sin \widehat{B})^2 = 1$
Enfin, la tangente d’un angle peut être définie à partir du sinus et du cosinus de l’angle :
$\tan \widehat{B} = \dfrac{\sin \widehat{B}}{\cos \widehat{B}}$
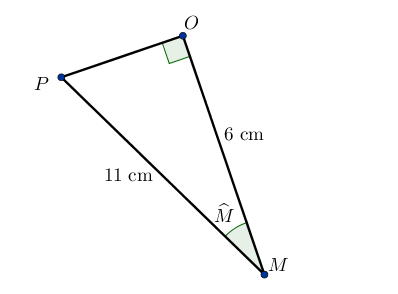
Exemple :
On cherche la valeur de l’angle $\widehat{M}$.
Il s’agit donc de déterminer si il faut utiliser le cosinus, le sinus ou la tangente.
Ici, l’hypoténuse est donné ainsi que le côté adjacent : on utilise donc le cosinus.
Ainsi, $\cos \widehat{M} = \dfrac{MO}{MP}$
$\cos \widehat{M} = \dfrac{6}{11}\approx 0,545$
Donc en utilisant la calculatrice pour déterminer l’angle en connaissant la valeur de son cosinus on trouve $\widehat{M} \approx 56,9°$
Trigonométrie : sinus
Trigonométrie
Sinus
Dans un triangle rectangle, le sinus d’un angle $\alpha$ est défini par :
$\sin(\alpha) = \dfrac{\text{côté opposé}}{\text{hypoténuse}}$.
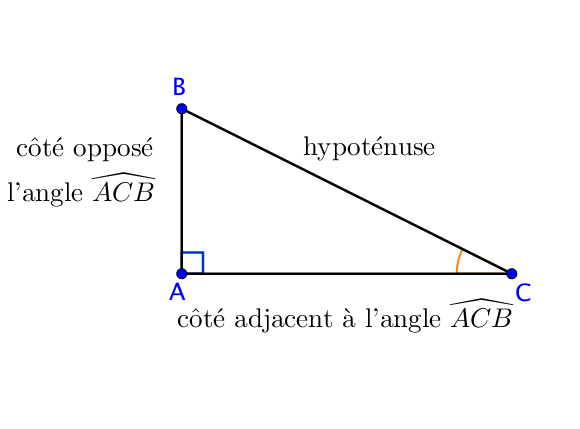
Exemple :
Dans le triangle $ABC$, rectangle en $A$, on veut calculer le sinus de l’angle $\widehat{ACB}$.
La première étape consiste à repérer sur la figure le côté opposé à l’angle $\widehat{ACB}$ qui est en face de l’angle, le côté adjacent à cet angle qui touche l’angle et l’hypoténuse qui est le plus grand côté, en face de l’angle droit.
La notion de côté opposé et de côté adjacent est une notion qui dépend de l’angle.
Ainsi,
$\sin(\widehat{ACB}) = \dfrac{AB}{BC}$.
Le sinus permet de calculer une longueur ou la mesure d’un angle.
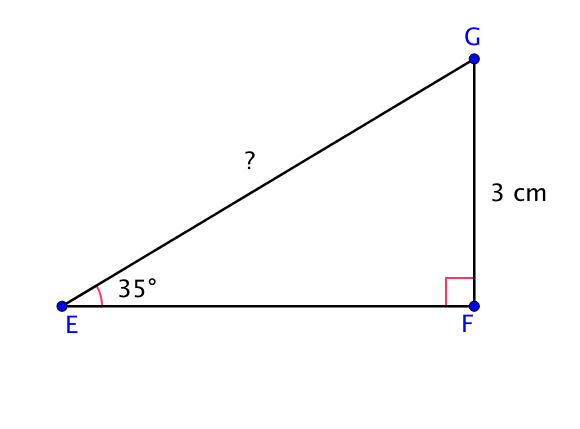
Exemple 1 : Calcul d’une longueur
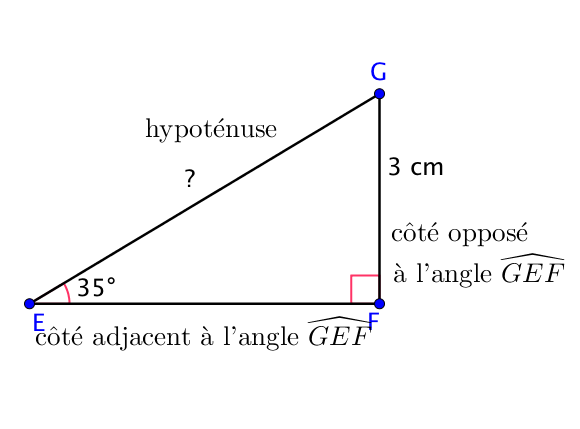
Soit $GEF$ un triangle rectangle en $F$, dont on connait la valeur de l’angle $\widehat{GEF}$ et la longueur $GF$.
On cherche la longueur $GE$.
On place ensuite sur le schéma le nom des différents côtés par rapport à l’angle dont on connait la mesure.
Comme on cherche l’hypoténuse en connaissant un angle et son côté opposé, la formule à utiliser est celle du sinus :
Dans le triangle $GEF$, rectangle en $F$,
$\sin(\widehat{GEF}) = \dfrac{GF}{GE}$
On remplace dans cette formule les mesures dont on dispose.
$\sin(35°) = \dfrac{3}{EG}$
Ainsi, $EG = \dfrac{3}{\sin(35°)}$.
On calcule enfin le résultat à l’aide de la calculatrice.
On donne une valeur approchée de $EG$ :
$EG \approx 5,2$cm.
Exemple 2 : Calcul de la mesure d’un angle
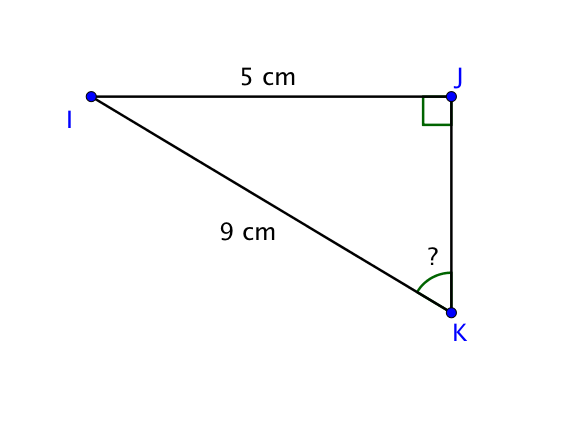
Soit $IJK$ un triangle rectangle en $J$, dont on connait les longueurs $IJ$ et $IK$. On cherche la mesure de l’angle $\widehat{IKJ}$.
On place sur le schéma le nom des côtés par rapport à l’angle $\widehat{IKJ}$.
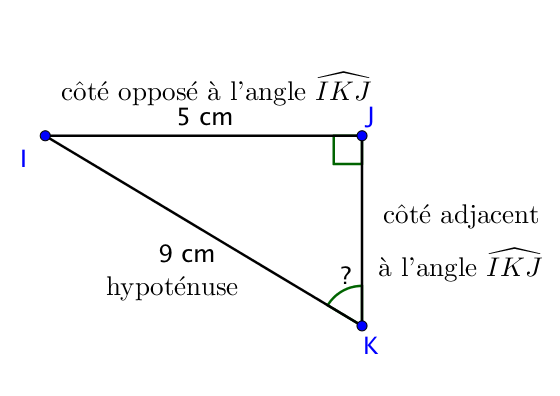
Connaissant le côté opposé et l’hypoténuse de l’angle $\widehat{IKJ}$ et cherchant sa valeur, on utilise la formule du sinus qui lie ces trois grandeurs.
Dans le triangle $IJK$, rectangle en $J$,
$\sin(\widehat{IKJ}) = \dfrac{IJ}{IK}$
En remplaçant par les mesures connues, à exprimer dans la même unité, on trouve :
$\sin(\widehat{IKJ}) = \dfrac{5}{9}$
On utilise la calculatrice pour calculer $\widehat{IKJ}$, en appuyant sur la touche $\arcsin$ ou $\sin^{-1}$ puis en rentrant la quotient $\dfrac{5}{9}$.
On trouve alors :
$\widehat{IKJ} \approx 34°$.
Trigonométrie : tangente
Trigonométrie – tangente
Définition
Dans un triangle rectangle, la tangente d’un angle aigu $\alpha$ vaut :
$\tan(\alpha) = \dfrac{\text{côté opposé}}{\text{côté adjacent}}$.
Exemple :
Soit $ABC$ un triangle rectangle en $B$.
On commence par repérer les côtés : le côté hypoténuse est le côté plus grand, en face de l’angle droit, le côté qui touche l’angle est le côté adjacent et le côté en face de l’angle est le côté opposé.
Ainsi, $\tan(\widehat{BAC}) = \dfrac{BC}{AB}$.
Cette formule permet de calculer soit une longueur, soit la mesure d’un angle.
Exemple 1 : Calcul d’une longueur
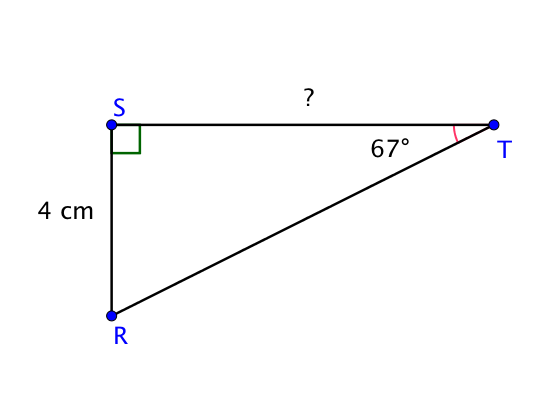
Soit $RST$ un triangle rectangle en $S$ dont on connait l’angle $\widehat{RTS}$ et la longueur du côté $[SR]$. On cherche la longueur du côté $[ST]$.
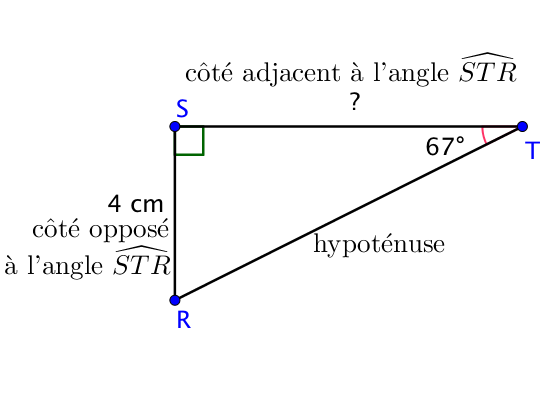
On commence par repérer les différents côtés.
La formule reliant le côté opposé, le côté adjacent et l’angle est la formule de la tangente.
Dans le triangle $RST$ rectangle en $S$.
$\tan(\widehat{RTS}) = \dfrac{SR}{ST}$.
On remplace les mesures que l’on connait.
$\tan(67°) = \dfrac{4}{ST}$.
Donc $ST = \dfrac{4}{\tan(67°)}$.
En utilisant la calculatrice, on trouve $ST \approx 1,7$cm.
Exemple 2 : Calcul de la mesure d’un angle
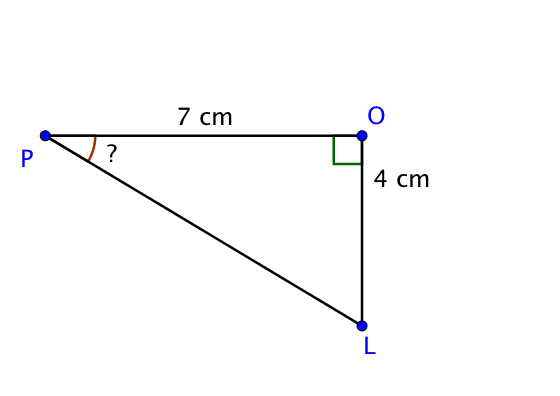
Soit $POL$ un triangle rectangle en $O$ dont on connait les longueurs $PO$ et $OL$ et dont on cherche la mesure de l’angle $\widehat{OPL}$.
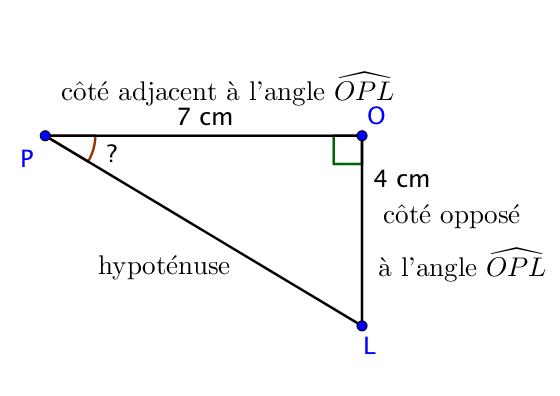
On commence par repérer les différents côtés.
La formule reliant le côté opposé, le côté adjacent et l’angle est la formule de la tangente.
Dans le triangle rectangle $POL$, rectangle en $O$,
$\tan(\widehat{OPL}) = \dfrac{OL}{OP}$
On remplace les mesures que l’on connait.
$\tan(\widehat{OPL}) = \dfrac{4}{7}$
On utilise la touche $\arctan$ ou $\tan^{-1}$ de la calculatrice pour avoir la mesure de l’angle $\widehat{OPL}$.
Ainsi, $\widehat{OPL} \approx 30°$.