Transformation chimique
On a représenté trois schémas avec : le triangle pour l’entité microscopique qui est contenue dans l’eau, le rond pour l’entité microscopique qui est comprise dans le sucre. A quoi correspondent ces trois transformations ?

Dans la première transformation, on a des entités disposées de manière organisée à gauche et désorganisée à droite, mais les entités n’ont pas changé entre le début et la fin de la transformation. Il s’agit d’une transformation physique qui est la fusion de l’eau par exemple.
Dans la deuxième transformation, on a le sucre à l’état solide ajouté dans de l’eau. On remarque qu’après la transformation, on a un mélange de sucre et d’eau qui est obtenu, mais les entités microscopiques n’ont pas été modifiées entre le début et la fin de la transformation.
Dans la troisième transformation, on a le cas d’une transformation chimique. Le mélange évolue pour donner de nouvelles entités qui n’étaient pas présentes au début. C’est une transformation chimique qui peut se détecter par l’apparition d’un solide, la disparition d’un solide, un dégagement gazeux, un changement de couleur, etc. Il y a différentes façons d’identifier une transformation chimique.
Une transformation chimique peut être écrite avec une équation de la réaction chimique. Les réactifs sont les espèces présentes avant la transformation chimique et les produits les espèces présentes après la transformation chimique. L’équation de la réaction chimique s’écrit de la manière suivante :
réactifs (+) → produits (+).
Exemple : la combustion du carbone
Les réactifs de la combustion du carbone (quand le carbone brûle) sont le carbone et le dioxygène. Le produit est le dioxyde de carbone. L’équation de la réaction chimique s’écrit, en toutes lettres, de la manière suivante : carbone + dioxygène → dioxyde de carbone.
On peut aussi écrire cette équation de la réaction chimique avec les formules chimiques des réactifs et des produits. Dans le cas du carbone, la formule chimique est C. Le dioxygène a pour formule O2 et le dioxyde de carbone CO2. On remarque dans cette équation chimique, et c’est le cas pour toutes les équations de réactions chimiques, qu’il y a le même nombre de carbone dans les réactifs et pour les produits. On remarque qu’il y a le même nombre d’oxygène dans les réactifs et dans les produits. On dit que, pendant une transformation chimique, les atomes se conservent.
Mesure de distance avec le son et la lumière
Mesure de distance avec le son et la lumière
I. Principe
On utilise deux propriétés du son et de la lumière : la propagation en ligne droite et la réflexion sur certains objets. Le principe de cette méthode pour mesurer des distances est le suivant :
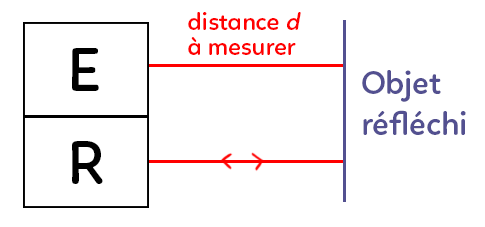
On place un émetteur et un récepteur au même endroit et un objet réflecteur situé à la distance que l’on doit mesurer. On envoie par l’émetteur un signal, qui peut être le son ou la lumière, qui va atteindre l’objet réflecteur puis ce signal va se réfléchir dans l’autre sens pour rejoindre le récepteur. On mesure alors la durée qu’il faut pour faire un aller-retour. Cette durée sera notée $∆t.$
Une fois la durée $∆t$ obtenue ainsi que la vitesse du son ou de la lumière dans le milieu, on peut déterminer la distance qui sépare l’émetteur et le récepteur de l’objet réflecteur.
Pour cela, on utilise la formule $vitesse = \dfrac{distance}{durée}$.
Dans notre cas : $v = \dfrac{2d}{∆t}$.
II. Distance Terre-Lune
Pour mesurer la distance Terre-Lune, les Hommes qui ont été sur la Lune ont mis un réflecteur dessus. On envoie depuis la Terre un signal laser qui part sur la Lune, se réfléchit puis revient sur la Terre.
La durée qu’il faut pour que ce faisceau laser fasse l’aller-retour est de 2,43 s.
Sachant que c = 300 000 km/s, pour calculer la distance on a :
$v = \dfrac{2d}{∆t}$ donc $2d = v\times ∆t$ alors $d = \dfrac{v\times ∆t}{2}$.
Donc : $d = \dfrac{300 000\times 2,43}{2} = 364 500 \ km$.
III. Sonar
Dans le cas du sonar, on utilise le son et même des ultrasons. Le bateau émet des ultrasons qui vont toucher les fonds marins dont on souhaite savoir la profondeur, puis les ultrasons se réfléchissent sur les fonds marins et reviennent sur le bateau.
Dans notre exemple, il faut 1,3 s pour faire l’aller-retour et donc pour déterminer la distance qui sépare le bateau et les fonds marins, on fait le même calcul mais cette fois-ci avec la vitesse des ultrasons :
$v = 1500 \ m/s$
$d = \dfrac{1500\times 1,3}{2} = 975 \ m$.


