Parallélogrammes particuliers
Parallélogrammes particuliers
I) Le rectangle
Pour démontrer qu’un quadrilatère est un rectangle, on peut d’abord montrer qu’il s’agit d’un parallélogramme (ou alors l’énoncé indique qu’il s’agit d’un parallélogramme) puis montrer que :
– soit il possède un angle droit
– soit ses diagonales sont de même longueur
Exemple :
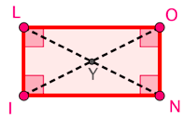
On sait que le quadrilatère $LINO$ est un parallélogramme.
On suppose tout d’abord que $\widehat{LIN} = 90°$.
Ainsi, $LINO$ est un rectangle.
On suppose maintenant que $LN=IO$. Or $[LN]$ et $[IO]$ sont les diagonales du parallélogramme.
$ABCD$ est donc un rectangle.
II) Le losange
Si un parallélogramme possède :
– deux côtés consécutifs de même longueur
OU BIEN
– des diagonales perpendiculaires
alors ce parallélogramme est un losange
Exemple :
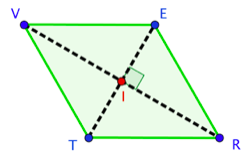
Soit $VERT$ un parallélogramme,
on suppose tout d’abord que $ER=RT$. Comme il s’agit de deux côtés consécutifs et qu’ils sont égaux, $VERT$ est un losange.
On suppose à présent que $(VR) \perp (TE)$. Or $[VR]$ et $[TE]$ sont les diagonales du parallélogramme, et sont perpendiculaires.
$VERT$ est donc un losange.
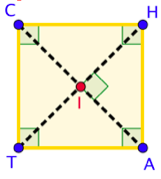
III) Le carré
Un carré est à la fois un rectangle et un losange.
Pour démontrer qu’un parallélogramme est un carré, il faudra suivre deux étapes.
La première consiste à montrer qu’il s’agit d’un rectangle en utilisant l’une des deux propriétés puis montrer qu’il s’agit d’un losange en utilisant l’une des deux propriétés.