Repérage dans un pavé droit
Repérage dans un pavé droit
On sait déjà se repérer sur une droite en utilisant l’abscisse d’un point et dans un repère en utilisant les abscisses et les ordonnées.
Définition :
Un repère dans un pavé droit est formé par $3$ arêtes qui ont un sommet en commun, appelé l’origine du repère.
Un point est repéré par ses coordonnées (abscisses; ordonnée; altitude).
Exemple :
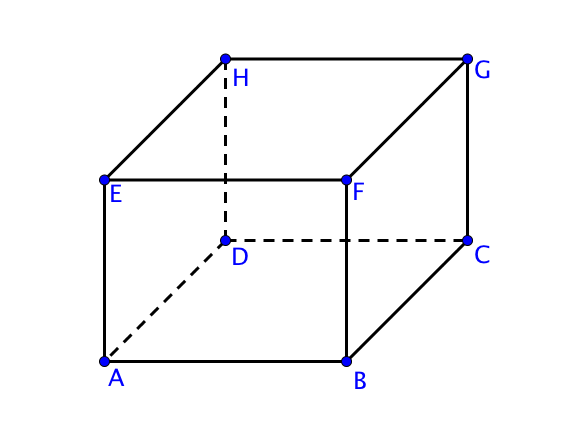
Soit le pavé droit $ABCDEFGH$.
On choisit ici comme origine du repère le point $A$. Les trois arêtes sont donc $AB$ (pour l’abscisse), $AD$ (pour l’ordonné) et $AE$ (pour l’altitude ou la hauteur).
On note le repère ainsi formé $(A; B; D; E)$. L’ordre est primordial et signifie que l’origine est le point $A$, le point $B$ détermine l’abscisse, le point $D$ détermine l’ordonné et le point $E$ l’altitude.
Pour donner les coordonnées on utilise trois nombres.
L’origine du repère a pour coordonnées $A(0; 0; 0)$ car on ne se déplace pas.
Pour aller de $A$ à $B$, on se déplace d’une unité selon les abscisses. Ainsi, $B(1; 0; 0)$.
Pour aller de $A$ à $D$, on se déplace seulement d’une unité selon les ordonnées, ainsi $D(0; 1; 0)$.
Pour aller de $A$ à $E$, on se déplace seulement d’une unité selon l’altitude, ainsi $E(0; 0; 1)$.
Pour aller de $A$ à $F$, on se déplace sur l’horizontal, en passant par $B$. Pour monter de $B$ à $F$ on monte de la même unité que pour aller de $A$ à $E$, ainsi, $F(1;0;1)$.
Pour aller de $A$ à $G$, on doit se déplacer de $1$ sur l’abscisse, de $1$ sur l’ordonné et de $1$ sur l’altitude, donc $G(1; 1; 1)$.
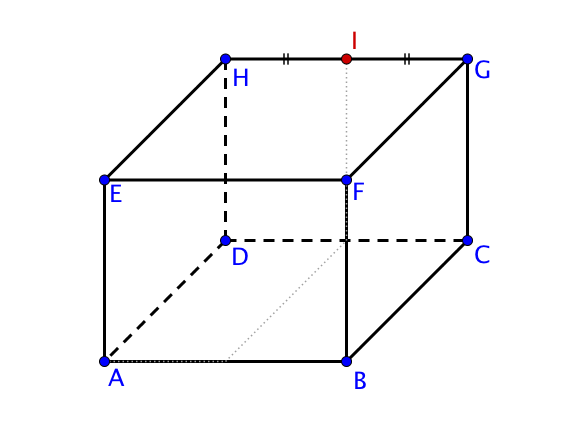
On s’intéresse maintenant au point $I$, milieu de côté $[HG]$.
Pour aller de $A$ à $I$, on se déplace de moitié sur l’abscisse, de $1$ selon les ordonnées puis on monte de $1$ selon l’altitude, ainsi $I(0,5; 1; 1)$.