Variations de fonctions exponentielles
Variations de fonctions exponentielles
Rappels
La fonction exponentielle peut se noter de diverses manières.
Elle est définie pour tout réel $x$ par $f(x) = \exp(x) = e^x$ avec $e = \exp(1) \approx 2,718$.
De plus, $f(0) = 1$.
En outre la dérivée de la fonction exponentielle est égale à la fonction elle même : on notera donc que $f'(x) = e^x$ pour tout $x \in \mathbb{R}$.
Enfin, on dispose de la propriété suivante :
Pour tout $x \in \mathbb{R}, \ e^x > 0$.
Comme $f'(x) = f(x)$ et que $f(x) > 0$, on peut conclure que la fonction $f$ est strictement croissante et positive sur $\mathbb{R}$.
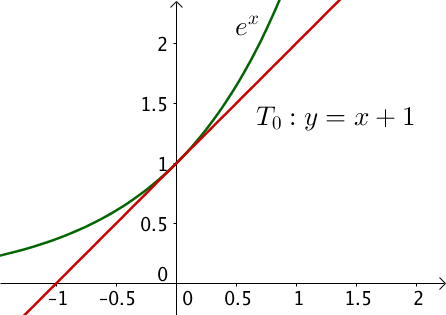
L’équation de la tangente à l’origine est :
$T_0 : y = f'(0)(x – 0) + f(0) = 1 \times x + 1 = x + 1$.
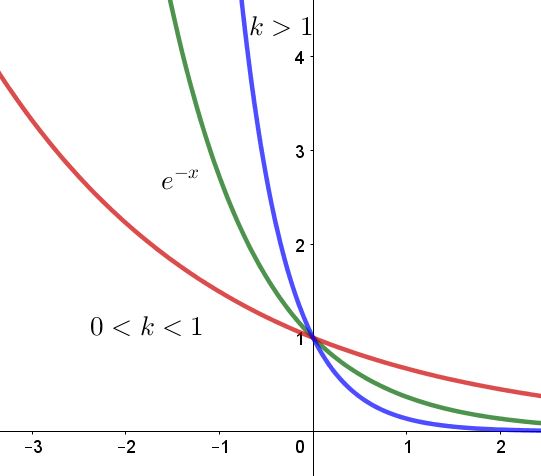
Les fonctions $f(x) = e^{-kx}$, avec $k$ un nombre réel strictement positif.
Soit $x \in \mathbb{R}$, on définit la fonction $f$ par $f(x) = e^{-kx}$, $k > 0$.
$f$ est dérivable pour tout réel $x$ et $f'(x) = -k e^{-kx}$.
Or $-k < 0$ et $e^{-kx} > 0$ par définition de l’exponentielle, on en déduit ainsi que $f'(x) < 0$.
La fonction $f$ est donc strictement décroissante.
Si $k >1$, la décroissance de $f$ est plus importante.
Toutes les fonctions passent par le point de coordonnées $(0; 1)$ car $f(0) = e^{-k \times 0} = 1$.
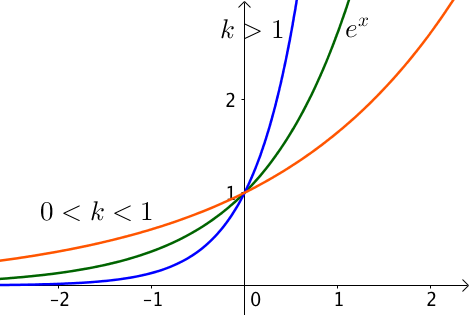
Les fonctions $f(x) = e^{kx}$, avec $k$ un nombre réel strictement positif.
Soit $x \in \mathbb{R}$, on définit la fonction $f$ par $f(x) = e^{kx}$, $k > 0$.
$f$ est dérivable pour tout réel $x$ et $f'(x) = k e^{kx}$.
Or $k > 0$ et $e^{kx} > 0$ par définition de l’exponentielle, on en déduit ainsi que $f'(x) > 0$.
La fonction $f$ est donc strictement croissante.
Si $k >1$, la croissance de $f$ est plus forte.
Toutes les fonctions passent par le point de coordonnées $(0; 1)$ car $f(0) = e^{k \times 0} = 1$.