Suites géométriques - Définition
I. Définition d’une suite géométrique
Qu’est-ce qu’une suite géométrique ?
Une suite géométrique est une suite pour laquelle chaque terme permet de déduire le suivant en étant multiplié par une constante $q$, la raison.
Une suite géométrique est ainsi définie par
$\left \{ \begin{array}{l} u_{n + 1} = u_n \times q \\ u_0 \\ \end{array} \right.$ où $q$ est la raison ($q \in \mathbb{R}$) et $u_0$ est le premier terme de la suite.
Considérons une suite géométrique de raison $2$ de premier terme 5 qui s’écrit alors :
$\left \{ \begin{array}{l} u_{n + 1} = u_n \times 2 \\ u_0=5 \\ \end{array} \right.$
Les premiers termes de la suite sont donc :
$u_1 = u_0 \times 2 = 5 \times 2 = 10$ et
$u_2 = u_1 \times 2 = 10 \times 2 = 20$.
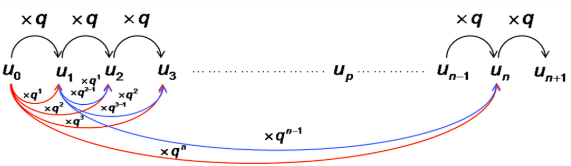
II. Propriété : expression de $u_n$ en fonction de $n$
Néanmoins la définition d’une suite géométrique nécessite pour calculer un terme de la suite d’avoir au préalable calculé tous les termes précédents.
Pour passer de $u_0$ à $u_n$, on remarque qu’il a fallu multiplier $u_0$ $n$ fois par $q$ :
Ainsi : $u_n = u_0 \times q^n$ pour tout $n \in \mathbb{N}$.
La formule plus générale permet de calculer tous les termes si l’on ne connait pas le premier terme mais le $p^{\text{ème}}$ :
Pour tous $n, \ p \in \mathbb{N}, u_n = u_p \times q^{(n – p)}$.
En reprenant l’exemple précédent, on trouve $u_4 = u_0 \times q^4 = 5 \times 2^4 = 80$
Montrer qu’une suite est géométrique
Comment montrer qu’une suite est géométrique ?
Afin de montrer qu’une suite $(u_n)$ est géométrique, on commence par calculer les premiers termes en s’assurant qu’ils ne sont pas nuls puis on calcule les rapports des premiers termes : $\dfrac{u_1}{u_0}$ et $\dfrac{u_2}{u_1}$.
Considérons par exemple la suite $u_n = 4 \times 3^n$. On a alors $\dfrac{u_1}{u_0} = 3$ et $\dfrac{u_2}{u_1} = 3$.
Si il apparait que le rapport des premiers termes est une constante $q$: on émet alors une conjecture en supposant que la constante ainsi trouvée est la raison de la suite.
Il faut alors montrer en revenant à la définition d’une suite géométrique que $u_{n + 1} = q \times u_n$ pour tout $n \in \mathbb{N}$.
En revenant à notre exemple, on souhaite montrer que $u_{n + 1} = 3 u_n$.
Or :
$3 u_n = 3 \times ( 4 \times 3^n ) $
$3 u_n= 4 \times 3^{n + 1} $
$3 u_n= u_{n + 1}$.
Donc $(u_n)$ est une suite géométrique de raison $3$ et de premier terme $u_0 = 4 \times 3^0 = 4 \times 1 = 4$.