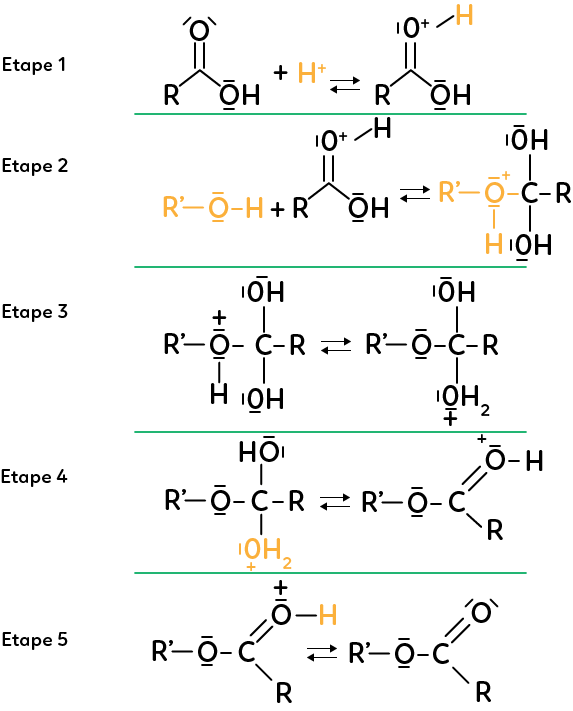
Mécanisme d'une réaction
Le mécanisme d’une réaction représente la suite chronologique des étapes se produisant lors de la transformation chimique. Le formalisme que l’on utilise pour représenter ce qu’il se passe lors d’un mécanisme réactionnel est le suivant : une flèche qui symbolise le mouvement des électrons du site donneur d’électrons vers le site accepteur d’électrons.
Exemple de la synthèse d’un ester
On représente le mécanisme de la synthèse d’un ester, aussi appelé estérification. Le jour du bac, on peut donner ce mécanisme qui doit être expliqué par les élèves en utilisant le formalisme.
Étape 1 :
La réaction d’estérification met en jeu un acide carboxylique et un alcool, le tout en milieu acide. La première étape est la réaction entre l’ion hydrogène et l’acide carboxylique. Le site donneur est le doublet de l’oxygène qui agit sur l’hydrogène.
Étape 2 :
L’alcool réagit avec l’espèce qui vient d’être créée. Le site donneur est l’oxygène, riche en électrons, qui réagit avec le carbone, pauvre en électrons car entouré d’atomes d’oxygène, plus électronégatifs que lui. Comme le carbone ne peut faire que quatre liaisons, on a un mouvement d’électrons du carbone vers l’oxygène voisin. Ces deux étapes, 1 et 2, sont des réactions d’addition successives.
Étape 3 :
On a ici une réaction intermoléculaire. Le doublet non liant de l’oxygène réagit avec le site accepteur qu’est l’hydrogène, étant moins électronégatif que l’oxygène. En réponse à cela, il y a un mouvement d’électrons de l’hydrogène vers l’oxygène voisin pour reformer le doublet non liant de l’espèce produite.
Étape 4 :
On a l’oxygène donneur d’électrons et le carbone accepteur. De plus, il y a éjection d’une partie de la molécule qui se dévoile être de l’eau. On a une réaction d’élimination.
Étape 5 :
L’hydrogène donne un électron à l’oxygène voisin. Il y a stabilisation de la molécule et formation d’un ester et d’un ion hydrogène.
On peut noter que l’ion hydrogène, qui permet une réaction en milieu acide, peut être caractérisé comme catalyseur. On a besoin de cet ion pour initier la réaction mais il est régénéré à la fin de la réaction.
Déterminer une quantité de matière
Déterminer une quantité de matière
Déterminer une quantité de matière c’est déterminer le nombre de moles $n$ qui s’exprime en $mol.$ On a :
• $M$ la masse molaire (masse d’une mole d’espèce chimique) qui s’exprime en $g.mol^{-1}.$ Les masses molaires atomiques sont précisées dans le tableau périodique et on les donnera. La masse molaire d’un ion est environ égal à la masse molaire de l’atome correspondant. Quand on a la masse molaire d’une molécule à déterminer, il suffit de faire la somme des masses molaires atomiques qui constituent cette molécule. Dans le cas de la molécule d’eau, ce sera :
$M(H_2O) = 2 \times M(H) + M(O)$.
Ensuite on utilise la masse $m$ qui s’exprime normalement en $kg$ mais en chimie on l’exprime couramment en $g.$
• $V$ le volume, qui normalement s’exprime en $m^3$ mais en chimie on l’exprime en $L.$
• $ρ$ la masse volumique qui s’exprime normalement en kg.m-3, mais on peut aussi la voir exprimée en $g.L^{-1}, kg.L^{-1}, g.mL^{-1}.$ Il faut savoir que les $kg.L^{-1}$ sont équivalents aux $g.mL^{-1}$ et quand on fait les conversions $L/m^3,$ il faut se souvenir de la relation qui permet de faire les conversions : $1 \ dm^3 = 1 \ L.$
• $C$ la concentration molaire qui s’exprime en $mol.L^{-1}.$
• $C_m$ (ou $t$ le titre massique) la concentration massique qui s’exprime en $kg.L^{-1}$ ou en $g.L^{-1}.$
Attention ! La concentration massique a la même unité que la masse volumique mais ce ne sont pas du tout les mêmes grandeurs. Pour la concentration massique, c’est la masse de soluté par litre de solution et pour la masse volumique, c’est la masse d’un litre d’espèce chimique mais c’est la même espèce chimique dans le cas de la masse volumique.
Voyons comment déterminer la quantité de matière dans le cas où l’on a une espèce solide, une espèce liquide ou une espèce en solution.
Espèces solides
Si on a une espèce solide, souvent, on nous donne la masse de solide. On va alors utiliser la formule : $n = \dfrac{m}{M}$.
C’est le cas le plus simple avec $n$ la quantité de matière en mol, $m$ la masse en $g$ et $M$ la masse molaire en $g.mol^{-1}.$ Les masses molaires sont très souvent données en $g.mol^{-1}$ donc si on a une masse en $kg$, il faut penser à la convertir en $g$ pour que les unités soient cohérentes. De manière générale, il faut toujours vérifier que les unités sont cohérentes.
Espèces liquides
Si on a une espèce liquide, on n’aura souvent pas la masse mais le volume. On reprend la formule : $n = \dfrac{m}{M}$.
Et puisqu’on n’a pas la masse mais le volume on va « convertir » la masse en volume en utilisant la masse volumique : $ ρ =\dfrac{m}{V}$.
On obtient alors la formule : $ n =\dfrac{ ρ\times V}{M}$.
Il faut alors faire attention car la masse volumique peut être exprimée dans différentes unités. Le nombre de moles $n$ s’exprime en mol, le volume $V$ en litres et la masse molaire $M $en $g.mol^{-1}.$ Il faut donc que la masse volumique soit en $g.L^{-1}$ pour que les unités soient cohérentes. Il faut bien penser à faire les conversions nécessaires.
Espèces en solution
Si on a une espèce en solution, on utilise la relation : $n = C\times V_{sol}$.
Le nombre de moles $n$ s’exprime toujours en mol, la concentration molaire est exprimée en $mol.L^{-1}$ et le volume de la solution doit être exprimé en $L,$ pour que les unités soient cohérentes. Parfois, on donne la concentration massique et non pas la concentration molaire. On peut trouver une relation entre la concentration massique et la concentration molaire.
Donc : $C_m = \dfrac{m}{V_{sol}}$.
Or la masse est aussi égale au nombre de moles multiplié par la masse molaire : $C_m = \dfrac{n\times M}{V_{sol}}$.
On reconnaît : $\dfrac{n}{V}$, l’expression de la concentration molaire.
On a alors : $n = C\times M$.
Le nombre de moles vaut : $n = n = \dfrac{C_m}{M} \times V_{sol}$.
Il n’est pas nécessaire d’apprendre cette formule par cœur, on pouvait la retrouver avec le raisonnement précédent. $n$ est le nombre de moles en $mol,$ $C_m$ est la concentration massique en $g.L^{-1},$ $M$ la masse molaire en $g.mol^{-1}$ et $V_{sol}$ le volume de la solution en $L.$
Si on a des doutes sur une formule, on peut vérifier qu’elle est cohérente en faisant une analyse dimensionnelle (en analysant les unités). Si la concentration massique est exprimée en $g.L^{-1},$ le volume de la solution est exprimé en $L,$ et la masse molaire s’exprime en $g.mol^{-1}.$ Les grammes se simplifient, $L$ et $L^{-1}$ se simplifient aussi, on obtient alors l’inverse des $mol^{-1}$ qui vaut des mol. C’est bien l’unité de $n.$ A priori, on sait que notre formule est cohérente.