Notion de probabilité
Notion de probabilité
Définitions
L’équiprobabilité signifie que toutes les issues possibles ont les mêmes chances d’apparaitre.
En considérant par exemple l’expérience aléatoire du lancé de dé, cela signifie que le dé n’est pas truqué et chaque nombre a la même chance d’apparaitre.
Dans ce cas, la probabilité d’un événement, c’est à dire la chance qu’a un événement de se produire, se calcule par la formule
$p =\dfrac{\text{nombre de cas favorables}}{\text{nombre de cas possibles}}$.
En outre, le nombre de cas favorables, nombre positif, est toujours inférieur au nombre de cas possibles, ainsi une probabilité est toujours comprise entre 0 et 1.
Remarques
Plus une probabilité est proche de 0, plus l’événement a peu de chance de se produire
Une probabilité nulle signifie que l’événement est impossible: il ne se produira jamais.
Plus une probabilité est proche de 1, plus l’événement a de forte chance de se réaliser.
Une probabilité égale à 1 signifie que l’événement est certain.
Exemple : On tire, au hasard, une carte dans un paquet de 32 cartes.
Comme il est indiqué que le tirage se fait au hasard, toutes les cartes ont la même chance d’apparaitre : c’est donc une situation d’équiprobabiltié.
$p(\text{“roi de coeur”}) = \dfrac{1}{32}$ car il n’y a qu’un roi de coeur dans un paquet de 32 cartes.
$p(\text{“coeur”}) = \dfrac{8}{32} = \dfrac{1}{4}$ car il y a 8 coeurs dans un paquet de 32 cartes.
$p(\text{“noir”}) = \dfrac{16}{32} = \dfrac{1}{2}$ car il y a 8 cartes pique et 8 cartes trèfles.
Moyenne d'une série statistique
Moyenne d’une série statistique
Considérons la série statistique constituée de sept termes suivantes représentant le poids de sept personnes :
65 ; 54 ; 84 ; 66 ; 84 ; 59 ; 70
La moyenne de cette série correspond au poids moyen.
Méthode de calcul
Afin de la calculer, il faut additionner tous les termes puis diviser le résultat par le nombre total de termes.
On trouve alors
$m = \dfrac{65 + 54 + …. + 70}{7} \approx 68, 857$
$m \approx 68, 9 $ kg au dixièmes près.
Solides et volumes
Fréquence
Fréquence
Définition
La fréquence d’une valeur dans une série statistique est donnée par la formule
$f = \dfrac{\text{effectif de la valeur}}{\text{effectif total}}$.
Exemple :
21 élèves pratiquent la danse dans une classe de 28. La fréquence des élèves pratiquant la danse est
$f = \dfrac{21}{28} = 0,75$.
Propriétés
Une fréquence est toujours positive (l’effectif ne peut être négatif) et inférieure à 1 (l’effectif du caractère que l’on considère ne peut être supérieur à l’effectif total).
Pour obtenir une fréquence en pourcentage, on multiplie le résultat par $100$
Dans le cas précédent, $0,75\times 100 = 75$% d’élèves pratiquent la danse dans la classe
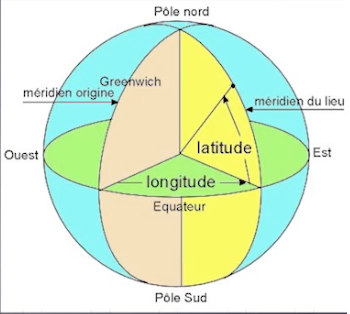
Latitude - longitude
Latitude – longitude
La latitude et la longitude permettent de se repérer sur le globe terrestre.
Définition : Parallèles
Ce sont des petits cercles parallèles à l’équateur, qui vont jusqu’aux pôles Nord et Sud.
L’hémisphère nord est la demi sphère au-dessus de l’équateur et l’hémisphère sud est la partie en dessous.
Pour repérer les parallèles, on utilise la latitude qui correspond à un angle compris entre $0°$ et $90°$, et d’une indication selon que l’on soit dans l’hémisphère nord ou l’hémisphère sud.
L’angle est formé par le segment reliant le centre de la Terre et l’équateur et le segment reliant le centre de la Terre et le parallèle considéré.
Il varie donc de $0°$ si on se situe sur l’équateur jusqu’à $90°$ si on est aux pôles. Il s’agit d’un angle vertical.
Définition : Méridiens
Ce sont de grands cercles passant par les deux pôles.
Le méridien le plus connu est celui de Greenwich, en Angleterre, qui sert d’origine pour tous les méridiens et c’est à partir de ce dernier que les décollages horaires sont fixés.
Pour repérer les méridiens, on définit la longitude qui correspond à un angle compris entre $0°$ et $180°$ et d’une indication Est ou Ouest selon le sens de rotation par rapport au méridien de Greenwich.
Il s’agit d’un angle horizontal.
Exemple :
35N 116E : La latitude vaut 35° vers le Nord et la longitude vaut 116° vers l’Est.