Positions relatives de deux droites
Positions relatives de deux droites
Une droite est un trait rectiligne illimité, c’est à dire qui peut toujours être prolongé, mais dont on en dessine qu’une partie.
Une droite peut aussi être définie comme un ensemble de points alignés, qui sont si rapprochés les uns des autres que l’on ne peut pas les distinguer.
La position relative des deux droites correspond à la position des deux droites l’une par rapport à l’autre.
Il existe différents cas possibles.
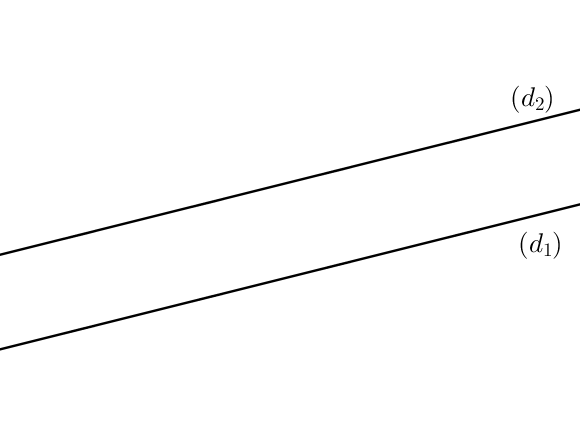
I) Les droites n’ont aucun point en commun.
C’est par exemple le cas des rails d’un train sur une portion droite : les rails ne se croisent jamais.
Dans ce cas, on peut prolonger les droites aussi loin qu’on le souhaite, il n’y aura jamais d’intersection.
On dit alors que les droites $(d_1)$ et $(d_2)$ sont parallèles et on note alors mathématiquement que $(d_1)//(d_2)$.
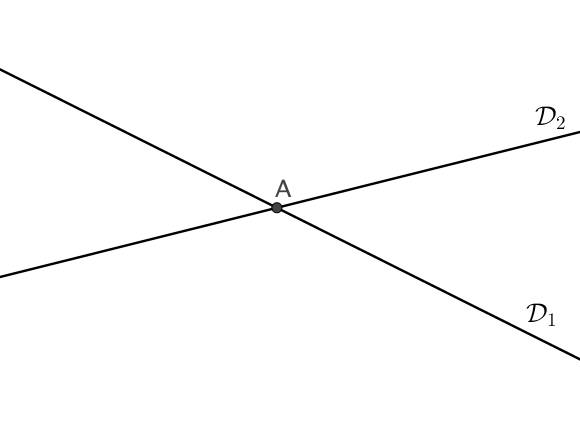
II) Les deux droites ont un unique point en commun.
Le point commun des droites $(\mathcal{D}_1)$ et $(\mathcal{D}_2)$ est le point $A$.
On dit alors que les droites $(\mathcal{D}_1)$ et $(\mathcal{D}_2)$ sont sécantes en $A$.
On dit aussi que le point $A$ est leur point d’intersection.
Cela signifie que le point $A$ appartient à la fois à la droite $(\mathcal{D}_1)$ et à la droite $(\mathcal{D}_2)$. Mathématiquement, on écrit $A \in (\mathcal{D}_1)$ et $A \in (\mathcal{D}_2)$.
Cas particulier :
Lorsque les droites se coupent, elles peuvent former un angle droit.
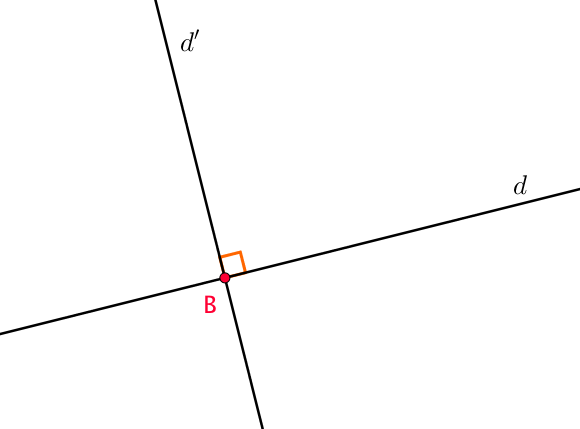
Exemple :
Les droites $(d)$ et $(d’)$ sont sécantes car elles ont un point commun B.
On dit que ces deux droites sont perpendiculaires car elles forment un angle droit en $B$ et on note mathématiquement que $d \perp d’$
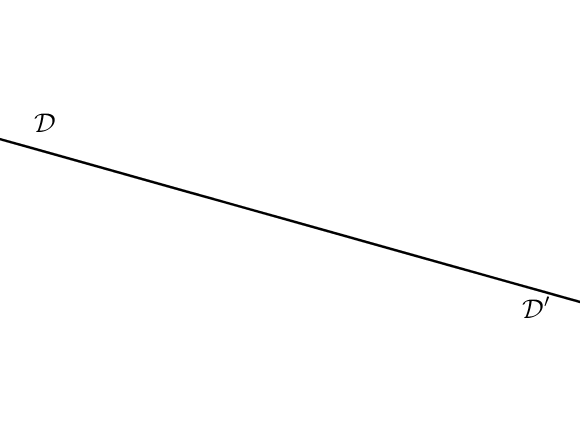
III) Les droites ont tous leurs points en commun.
Dans ce cas, on ne verra alors plus qu’une seule droite et on dira que $\mathcal{D}$ et $\mathcal{D’}$ sont confondues.