Décompositions de vecteurs dans une base
Décompositions de vecteurs dans une base
Décompositions de vecteurs dans une base
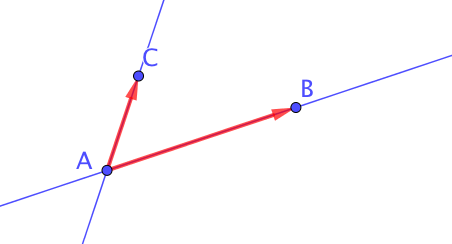
Lorsque trois points $A, B$ et$ C$ sont non alignés, le triplet $(A; \overrightarrow{AB}; \overrightarrow{AC})$ forme un repère du plan.
Les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ forment une base du plan et $A$ est l’origine du repère.
Pour mieux visualiser le repère, on peut tracer les axes qui sont les droites $(AB)$ et $(AC)$.
A partir d’un repère quelconque, il est possible de définir les coordonnées d’un point et ceux d’un vecteur.
Théorème
Soit $M$ un point quelconque du plan,
Alors il existe un unique couple de nombres $(x; y)$ tel que $\overrightarrow{AM} = x \overrightarrow{AB} + y \overrightarrow{AC}$.
Le couple $(x; y)$ est les coordonnées de $M$ dans le repère $(A; \overrightarrow{AB}; \overrightarrow{AC})$.
Soit $\overrightarrow{u}$ un vecteur du plan,
Alors il existe un unique couple de nombres $(x; y)$ tel que $\overrightarrow{u} = x \overrightarrow{AB} + y \overrightarrow{AC}$.
Le couple $\left( \begin{array}{c} x \\ y\\ \end{array} \right)$ est les coordonnées de $\overrightarrow{u}$ dans le repère $(A; \overrightarrow{AB}; \overrightarrow{AC})$.
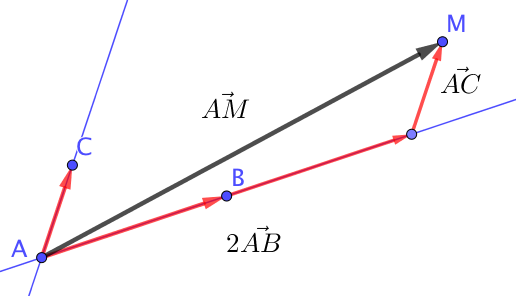
Si l’on doit placer le point $M(2; 1)$, il faut revenir à la définition, c’est à dire $\overrightarrow{AM} = 2 \overrightarrow{AB} + 1 \overrightarrow{AC}$.
On commence alors à tracer le vecteur $2 \overrightarrow{AB}$ puis on lui ajoute $1 \overrightarrow{AC}$, par la méthode des parallélogrammes car les deux vecteurs ont la même origine.
Le vecteur $\overrightarrow{AM}$ est donc la diagonale du parallélogramme ainsi construit et le point $M$ est à l’extrémité de ce vecteur.
Une telle définition permet de se placer désormais dans n’importe quel repère, et donc à partir de n‘importe quelle configuration géométrique, il est possible de définir un repère, permettant de travailler avec les coordonnées.
