Fonction valeur absolue

Fonction valeur absolue

Fonction Valeur absolue

Définition

La fonction valeur absolue est une fonction définie sur $\mathbb{R}$ à valeur dans $\mathbb{R}^+$ et on la note $\left \{ \begin{array}{ccccc} f & : & \mathbb{R} & \to & \mathbb{R}^+ \\ & & x & \mapsto & |x| \end{array} \right.$.

La valeur absolue d’un nombre positif est le nombre lui-même.

La valeur absolue d’un nombre négatif est son opposé. 

En d’autres termes,

Si $x \geq 0, \ |x| = x$

Si $x \leq 0, \ |x| = -x$

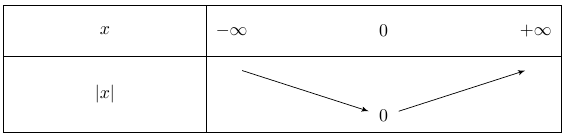
La fonction est strictement décroissante pour $x$ négatif et strictement croissante pour $x$ positif. 

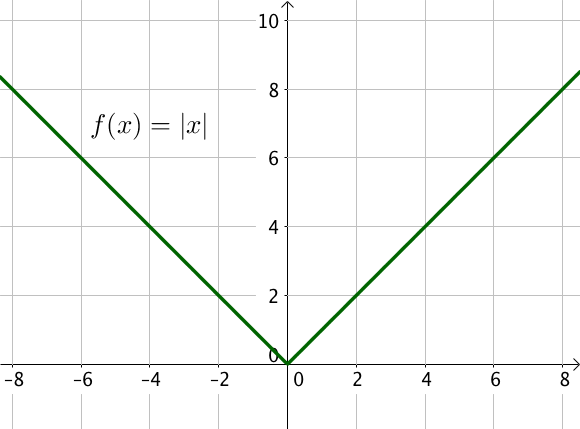
Sa représentation graphique est la suivante :

Propriétés 

Pour tout $x \in \mathbb{R}, \sqrt{x^2} = |x|$. 

Par exemple, $\sqrt{(-4)^2} = 4 = |-4|$. 

Exemples :

$|-5| = 5$

$|7| = 7$

$|\sqrt{2} – 5| = – \sqrt{2} + 5$

$|\pi + 2| = \pi + 2$

$|\pi – 4| = 4 – \pi$

Pour étudier la fonction $f(x) = |x + 3|$, on étudie le signe de $x + 3$ en s’aidant d’un tableau de signe.

Si $x + 3 \geq 0$ alors $f(x) = x + 3$. Si $x + 3 \leq 0$ alors $f(x) = -(x + 3)$.