Image d'un nombre par une fonction
Image d’un nombre par une fonction
Notion intuitive d’image
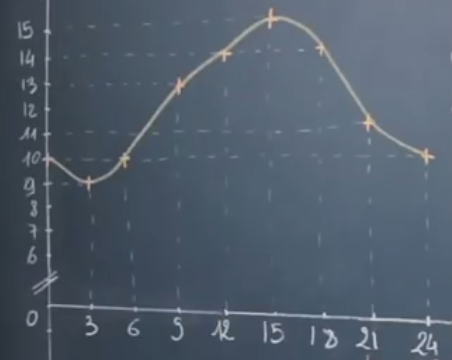
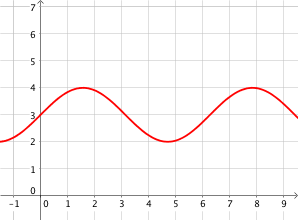
Considérons la courbe de température suivante :
L‘ensemble de définition de la fonction est $[0, 24]$, c’est à dire que l’étude se fait sur une journée complète à partir de minuit.
L’ordonnée est la température, il s’agit donc de la représentation graphique de la température en fonction du temps.
Ainsi, le temps est sur l’axe des abscisses.
Question : quelle température faisait-il à 3h du matin ?
On lit graphiquement que la température à 3h du matin est 9°C.
Ainsi, on dira que l’image de 3 par la fonction $f$ vaut 9 : il n’y a plus d’unité. On notera aussi $f(3) = 9$.
Définition
Soit $f$ une fonction et $a$ et $b$ deux réels vérifiants $f(a)=b$.
On dit que $b$ est l’image de $a$ par $f$.
Ou encore : l’image de $a$ par $f$ vaut $b$.
Autre exemple :
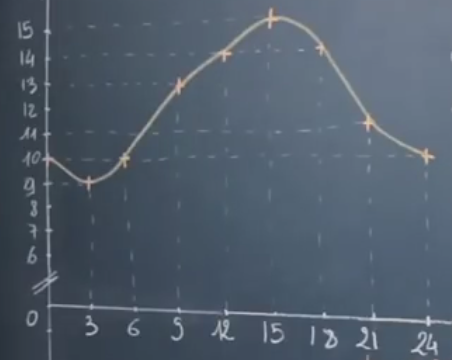
Pour trouver l’image de 15, on se place sur l’axe des abscisses à $t = 15$ puis on trace la droite perpendiculaire à cet axe et on regarde l’ordonnée du point d’intersection entre cette droite et la courbe de $f$ :
On lit $f(15) = 15$.
Antécédent d'un nombre par une fonction
Antécédent d’un nombre par une fonction
Définition
Soit $f$ une fonction et deux réels $a$ et $b$ vérifiant $f(a)=b$
On dit que $b$ est l’image de $a$ par $f$. (c’est une valeur unique)
On dit que $a$ est un antécédent par $f$ de $b$. (il peut y en avoir plusieurs)
Exemples
Cherchons le ou les antécédents, s’ils existent de $14$
Cela revient à chercher l’heure à laquelle la température était de 14°C.
Pour ce faire, on se place sur l’axe des ordonnées (l’axe des températures ici) et on trace la droite perpendiculaire à cet axe puis on regarde les points d’intersection entre la droite et la courbe de température et finalement, on lit leur abscisse.
Ici, il y a deux points d’intersections pour lesquels la température est de 14°C et donc deux heures différentes : 12h et 18h.
Il se peut que dans certains cas il n’y ait aucune solution.
Mathématiquement, le fait qu’il ait fait 14°C à 12h et 18h se traduit par :
Les antécédents de 14 par la fonction $f$ sont 12 et 18.
Ou encore : les solutions de l’équation $f(t) = 14$ sont $S = \{12; 18\}$.
Considérons l’équation $f(t) = 10$ : on cherche donc les antécédents de 10 par $f$.
Les solutions sont donc $S = \{0; 6; 24\}$.
Considérons l’équation $f(t) = 16$ : on cherche donc les antécédents de 16 par $f$.
La température de 16°C n’étant jamais atteinte, cette équation n’admet pas de solution :
$S = \varnothing$.
Notions de fonctions
Notions de fonctions
Découvrir les fonctions
On se place dans une salle et on mesure la température durant plusieurs heures.
Pour introduire la notion de fonction, on peut tout d’abord se demander quel graphique représente le mieux l’évolution de la température au cours du temps.
a)
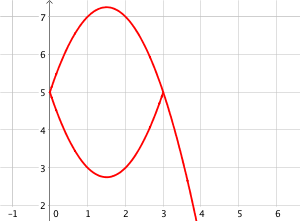
Cette représentation graphique ne peut convenir car pour un même temps correspond deux valeurs différentes de températures.
Un nombre admet une unique image par une fonction.
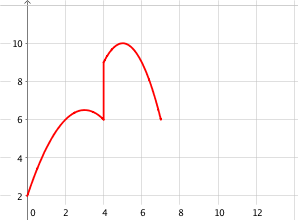
b)
Cette représentation ne peut convenir car aux alentours de 4 heures, il y a plusieurs valeurs possibles de températures.
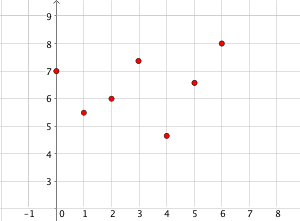
c)
Cette représentation est un nuage de points et ne correspond pas à une fonction définie sur un intervalle réel mais sur les entiers naturels.
d)
Cette représentation convient : il s’agit donc d’une fonction, à un point est associé une image.
En d’autres termes, pour un point sur l’axe des abscisses correspond un unique point sur l’axe des ordonnées.
Définition
Une fonction est notée :
$\begin{array}{ccccc}
& & I & \to & J \\
f & : & x & \mapsto & f(x) \\
\end{array}$, qui signifie qu’il est associé à un nombre $x$ son image $f(x)$ par la fonction $f$. $I$ et $J$ sont deux intervalles.
Le nombre $x$ s’appelle la variable. Dans les exemples précédents, la variable était le temps.
On dit que l’on exprime $f(x)$ en fonction de $x$ : dans les exemples, on a exprimé la température en fonction du temps.
Ce qui vient après “en fonction de” est toujours placé sur l’axe des abscisses.
L‘ensemble de définition est l’ensemble des valeurs pour lesquelles la fonction existe et est noté $D$ ou $D_f$.