K-uplets et permutations
k-uplets et permutations
Définition
Soit $E={x_1,x_2,…,x_n}$ un ensemble à n éléments.
On appelle k-uplet d’éléments distincts l’objet mathématique :
$(x_1,x_2,…,x_k)$ avec $1\leq k\leq n$ .
C’est une sélection de k objets sélectionnés parmi les objets de l’ensemble E. Les objets sont 2 à 2 distincts : pour tout i,j, $x_i\ne x_j$.
Ainsi, lorsque que l’on construit le k-uplet, on ne peut pas reprendre plusieurs fois le même objet de E.
Dans le k-uplet, l’ordre compte : $(x_1 ;x_2 ;… ;x_k)\neq (x_2 ;x_1 ;… ;x_k)$ et il n’y a pas de répétition possible.
Former un k-uplet dans un ensemble à n élément correspond en quelque sorte à piocher k billes dans un sac de n bille, chaque bille piochée est mise de coté. Un k-uplet s’appelle aussi un arrangement à k élément parmi n.
En formant le k-uplet, on a n choix pour piocher le premier élément (on prend 1 élément dans n élément).
On a ensuite n-1 choix pour le second, (on peut piocher parmi tous les élément sauf celui que l’on vient de piocher) et ainsi de suite.
Pour le k-ième, k-1 éléments ont déjà été choisis, il reste :
$n-(k-1)=n-k+1$ choix possibles.
On peut donc appliquer le principe multiplicatif :
Le nombre de k-uplets possible dans un ensemble à n éléments est :
$A_n^k=n(n-1)(n-2)…(n-k+1)$
$A_n^k=\dfrac{n(n-1)…(n-k+1)(n-k)(n-k-1)…1}{(n-k)(n-k-1)…1}$
$A_n^k=\dfrac{n!}{(n-k) !}$ valable pour $0\leq k\leq n$
Exemple :
12 chevaux s’élancent, le but est de trouver le nombre de tiercé dans l’ordre.
Donc pour le premier cheval, 12 possibilités, 11 pour le deuxième, 10 pour le dernier.
Il y a donc $12 \times 11\times 10 = 1320$ possibilité pour un 3-uplet dans un ensemble à 12 éléments.
Cas particulier :
Si k=n, le n-uplet est une permutation. On appelle cela une permutation, car pour former le n-uplet, vous prenez les n éléments de l’ensemble à n éléments et vous les écrivez dans un ordre différent. Vous avez simplement permuté certains éléments.
Vous avez n choix pour le premier, n-1 pour le deuxième… et 1 choix pour le dernier.
Donc le nombre de permutation est n!, ce que l’on retrouve aussi avec la formule ci-dessus : $E=\frac{n!}{0!}=n!$
Exemple :
Anatole, Judith et Apolline s’assoient sur un banc à 3 places.
Judith à 3 possibilité pour s’assoir, Anatole à elle plus que 2 possibilité pour s’assoir, et Apolline n’a plus le choix et doit prendre la place restante.
$3!=6$ : il y a 6 possibilités d’assoir 3 personnes sur un banc à 3 places.
n- uplets de (0, 1)
$n$-uplets de $(0, 1)$
On s’intéresse ici au nombre de $n$ uplets ($n \in \mathbb{N}^*$) pouvant être construits à partir de $2$ éléments : 0 et 1.
Un exemple de $n$-uplet est $(0, 1, 1, 0, …, 1)$.
On remarque alors que l’ordre d’apparition doit être considéré et qu’il peut y avoir répétition.
Pour chaque élément du $n$-uplet, il existe deux choix possibles (0 ou 1).
En appliquant le principe multiplicatif pour les $n$ éléments, on trouve qu’il existe $\underbrace{2 \times 2 \times … \times 2}_{n} = 2^n$ $n$-uplets de $\{0; 1\}$.
Exemples :
On considère dans un premier temps un alphabet à 2 lettres. Un mot de $n$ lettres est un $n$-uplet.
Il y a donc $2^n$ mots de $n$ lettres lorsqu’il existe deux lettres dans l’alphabet.
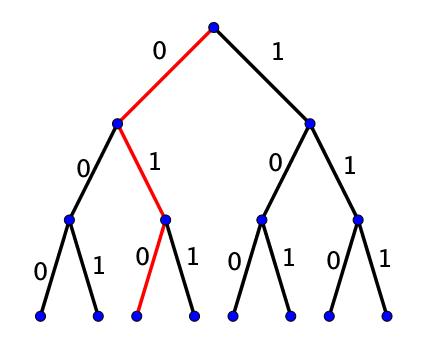
On peut aussi s’intéresser à un arbre avec deux choix possibles à chaque étape. On se demande le nombre de chemins que l’on peut parcourir en partant de la racine jusqu’à l’extrémité d’une des feuilles.
Pour se faire, on remarque qu’à chaque arrêt, il existe deux choix possibles : suivre le chemin de gauche, que l’on symbolise par un 0, ou alors le chemin de droite, symbolisé par un 1.
Un chemin peut être assimilé à un $3$-uplet (ou triplet).
Ainsi, le nombre de chemins possibles correspond au nombre de $n$ uplets que l’on peut former avec des $0$ et des $1$.
Puisque $n = 3$ dans l’exemple, il y a donc $2^3 = 8$ chemins possibles.
Enfin, le dernier exemple traite de la répétition de $n$ épreuves de Bernoulli ayant deux issues $\{0; 1\}$ (Succès ou Echec).
La répétition peut être codée par un $n$-uplet représentant chacun des choix à l’issue des $n$ épreuves.
Le nombre de répétitions est le même que le nombre de $n$-uplets constitués de $0$ ou de $1$, à savoir $2^n$.