Lumière : onde ou particule ?
La lumière est-elle une onde ou une particule ?
On sait déjà que la lumière peut être considérée comme une particule, avec notamment, l’effet photoélectrique. C’est une particule particulière de lumière appelée photon. Et on a vu aussi que la lumière peut être considérée comme une onde avec les phénomènes d’interférences et de diffraction.
Quelles sont les formules à retenir pour l’aspect particulaire de la lumière ?
Il y a la formule de l’énergie d’un photon : $E = h\times ν = \dfrac{h\times c}{\lambda}$
L’énergie est en joules (J), c est la constante de la vitesse de la lumière dans le vide (3,00.108 m.s-1), $h$ la constante de Planck est donnée dans les exercices avec plus ou moins de chiffres significatifs (6,63.10-34 J.s, on a trois chiffres significatifs pour être cohérents avec le nombre de chiffres significatifs de $c$), $\lambda$ a longueur d’onde en mètres (m).
Pour rappel, la longueur d’onde caractérise la couleur de l’onde, donc la couleur du photon. Ce qu’il faut comprendre dans cette formule, c’est le rapport entre la longueur d’onde et l’énergie. Quand la longueur d’onde est petite, l’énergie est grande, dû à l’inverse de la proportionnalité. Inversement, si la longueur d’onde est grande, l’énergie va être petite. Dans les exercices, il faut trouver l’énergie grâce à la longueur d’onde.
La relation qui s’ajoute à cela est la relation de Louis de Broglie :
$p = m\times v$ et $p = \dfrac{h}{\lambda}$
Les relations font intervenir : $p$, l’impulsion, $h$ la constante de Planck et $\lambda$ la longueur d’onde. Ces sont des relations qu’il faut connaître. Elles font le lien entre la lumière qui correspond à une particule et la lumière qui correspond à une onde. Les phénomènes ondulatoires vus sur les chapitres sur l’interférence et la diffraction ne sont observables que sur des petites longueurs d’ondes. Donc, ici, si la longueur d’onde est petite, l’impulsion correspondante sera grande.
Ce qui est intéressant avec cette formule c’est qu’elle est valable pour toutes les particules (pas seulement pour la lumière) comme les électrons, par exemple. Si la longueur d’onde est grande, l’impulsion va être petite. Et, si la longueur d’onde est grande, on observera plus de phénomène ondulatoire mais on n’observera seulement des effets particulaires.
Qu’est-ce que l’effet photoélectrique ?
Qu’est-ce que l’effet photoélectrique ?
Pour comprendre l’effet photoélectrique, il faut s’intéresser à deux notions : les corps noirs et la théorie des quantas de Max Planck.
Qu’est-ce qu’un corps noir ?
On trouve plusieurs descriptions dans la littérature. C’est un corps dans lequel on envoie un type de rayonnement (cela ressemble un peu à un four), et ce rayonnement est totalement absorbé par les parois du four. C’est un corps qui est parfaitement absorbant et lorsqu’on le chauffe, le rayonnement émis par le fait que l’on chauffe ce corps noir dépend totalement des propriétés des parois (de ce four) de ce corps noir.
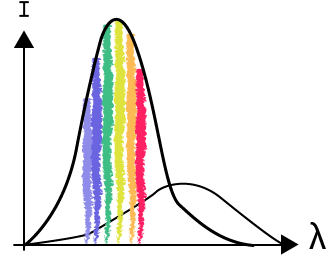
À partir de cette théorie du corps noir, on a essayé de traduire le lien entre intensité lumineuse, couleur (longueur d’onde) et température. C’est ce que l’on connaît sous le nom de la loi de Wien.
Lorsqu’on a la courbe de faible température et lorsqu’on augmente la température du corps noir, l’intensité lumineuse augmente et elle est suivie d’un décalage vers les courtes longueurs d’ondes. Plus le corps est chauffé, plus il va émettre vers les faibles longueurs d’ondes. Un moyen mnémotechnique pour s’en rappeler : lorsqu’on prend la flamme d’un briquet, la partie haute jaune de la flamme est beaucoup moins chaude que la partie bleue du centre. Plus on chauffe, plus on se décale vers le bleu et le violet et donc les faibles longueurs d’ondes.
Théorie des quantas
Qu’est-ce que la théorie des quantas ?
Cette loi de Wien pose des problèmes à Planck au début du XXe siècle puisqu’elle rend assez mal compte de ce qui se passe pour les grandes longueurs d’ondes. Planck va mettre au point la théorie des quantas pour décrire au mieux ce phénomène. Il va dire que le corps noir est capable d’absorber l’énergie par paquet et ce paquet d’énergie vaut : $E = h \times ν$, avec $E$ le paquet d’énergie en joules, $h$ la constante de Planck en J.s et $ν$ la fréquence du photon émis ou absorbé en s-1.
Cette théorie des quantas est développée pour permettre d’expliquer au mieux possible cette loi de Wien. À l’époque, quand Planck développe cette théorie, on n’est pas sûr que l’atome existe vraiment. On n’est pas sûr non plus des implications de ce type de loi. Les applications seront reprises par Einstein et c’est ce que l’on va justement appeler l’effet photoélectrique. C’est un phénomène que l’on a déjà étudié au XIXe siècle mais qui sera compris par Einstein et celui-ci sera récompensé pour ses travaux sur l’effet photoélectrique en 1921 avec son prix Nobel.
L’effet photoélectrique
Quels sont les types d’effet photoélectrique ?
Il existe deux types d’effet photoélectrique : l’effet photovoltaïque, lié aux panneaux photovoltaïques (panneaux solaires) où l’on transforme de l’énergie lumineuse en énergie électrique et l’émission photoélectrique dont le principe est le suivant.
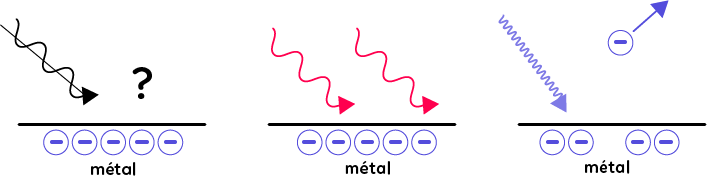
Quand on envoie de la lumière sur un métal, dans certaines conditions, il peut se passer des phénomènes mais cela dépend du type de lumière envoyée, de la longueur d’onde de la lumière. Si on envoie de la lumière rouge correspondante aux grandes longueurs d’onde, cette lumière ne peut pas avoir d’influence sur le métal. Par contre, lorsqu’on envoie de la lumière violette, on observe que les électrons du métal sont arrachés facilement de ce métal. C’est ce qu’on appelle l’émission photoélectrique.
Einstein reprend le concept de quantas de Planck pour expliquer ce phénomène et donc il modifie un peu la formule en faisant un lien entre l’énergie (concept du photon) qui est plus ou moins énergétique selon sa longueur d’onde.
On a alors : $E = \dfrac{h \times c}{λ}$.
On se rend compte par cette formule que plus la longueur d’onde diminue, plus l’énergie augmente. C’est-à-dire que les photons qui correspondent à une longueur d’onde faible, par exemple les photons violets, sont plus énergétiques que les photons de grande longueur d’onde (photons rouges). Si les électrons ont une fréquence suffisamment élevée, il y a émission d’électrons.