Positions relatives de droites
Positions relatives de droites
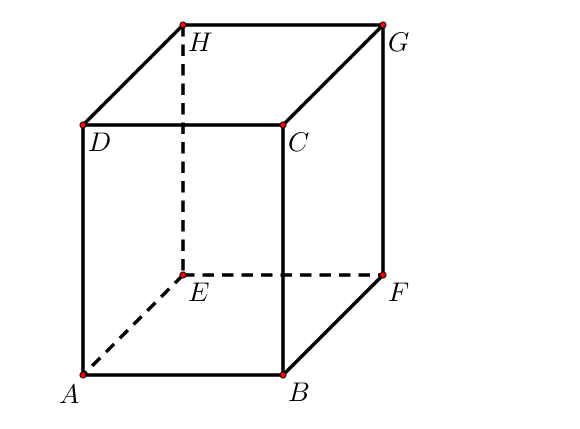
Il existe 4 cas différents pour décrire la position relative de droites dans l’espace. (c’est à dire comment est l’une par rapport à l’autre)
1) Les droites peuvent être parallèles, et forment un plan dans ce cas. On dit qu’elles sont coplanaires.
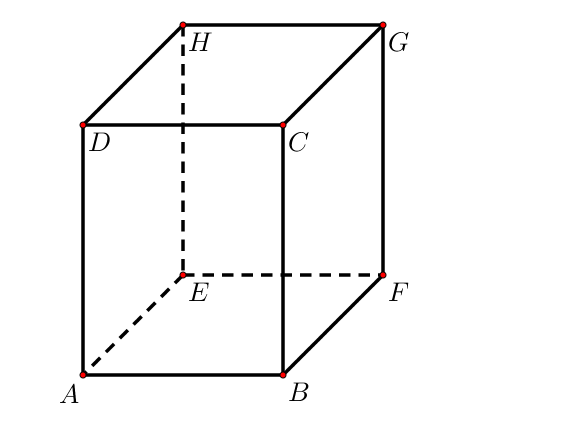
Par exemple, les droites $(HD)$ et $(GC)$ sont parallèles.
2) Deux droites peuvent être confondues.
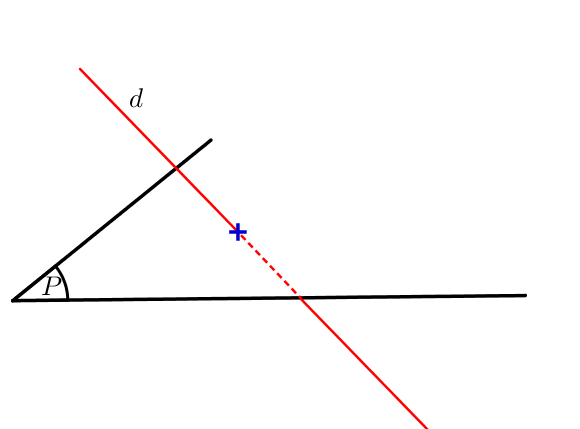
3) Deux droites peuvent être également sécantes et sont coplanaires.
C’est le cas par exemple des droites $(AB)$ et $(BF)$
4) Enfin deux droites peuvent être non coplanaires.
Par exemple, les droites $(BC)$ et $(DH)$ ne sont pas dans le même plan, elles ne sont donc pas coplanaires.
Positions relatives de plans
Positions relatives de plans
On décrit ici les différentes positives relatives de plans.
1) Deux plans peuvent être confondus, c’est à dire que les deux faces sont l’une sur l’autre.
2) Deux plans peuvent être parallèles.
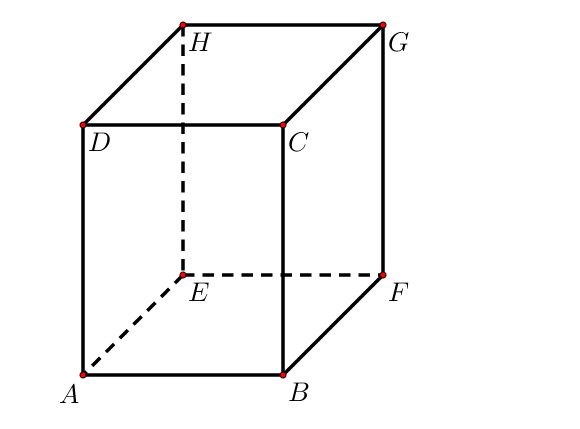
Sur le cube, les faces $ABFE$ et $DCGH$ sont parallèles.
3) Enfin, deux plans peuvent être sécants et leur intersection est une droite.
Sur le cube, les faces $ABFE$ et $BFGC$ sont sécantes et se coupent selon la droite $(BF)$.
Il s’agit du cas le plus fréquent et il faudra dans la plupart des exercices de trouver la droite d’intersection.
Positions relatives de droites et plans
Positions relatives de droites et plans
On cherche à décrire la position relative d’une droite et d’un plan.
1) Une droite et un plan peuvent être sécants, dans ce cas, leur intersection est un point.
C’est par exemple le cas de la face $ABFE$ du cube et la droite $(GA)$, le point d’intersection est le point $A$.
2) Une droite peut également être incluse dans le plan
Comme c’est le cas pour la droite $(HE)$ dans le plan $HEFG$ du cube.
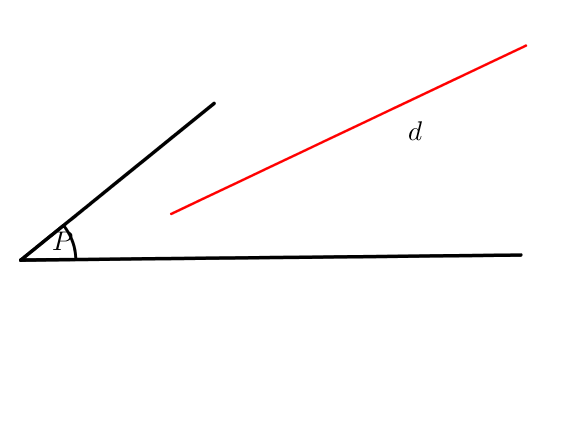
3) Enfin une droite peut être parallèle au plan.
Pour prouver cette position, on peut démontrer le parallélisme entre une droite incluse dans le plan et la droite que l’on étudie.
Par exemple, la droite $(DC)$ du cube est parallèle à la face $ABFE$.
En effet, les droites $(DC)$ et $(AB)$ sont parallèles et la droite $(AB)$ est incluse dans la face $ABFE$.
Plans parallèles
Plans parallèles
Théorème :
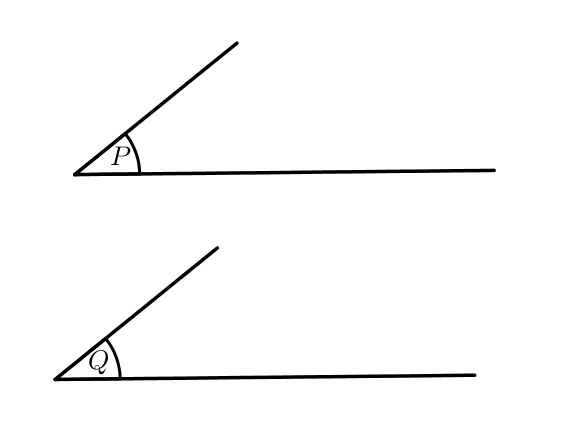
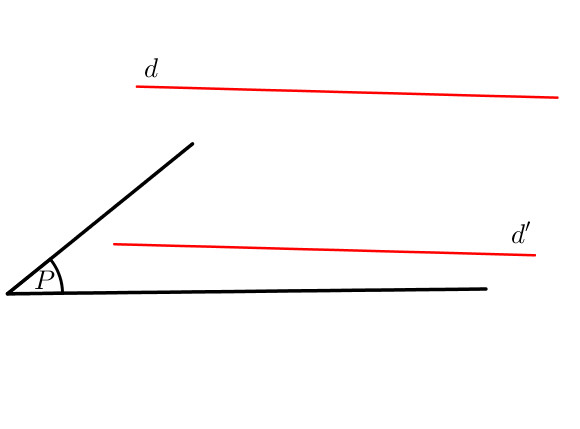
Soient $(P)$ et $(Q)$ deux plans de l’espace,
$d$ et $\Delta$ deux droites sécantes du plan $(P)$,
$d’$ et $\Delta ‘$ deux droites sécantes du plan $(Q)$,
Si $\left \{ \begin{array}{l} d \ // \ d’ \\ \Delta \ // \ \Delta ‘ \end{array} \right. $, alors $(P)\ // \ (Q)$.
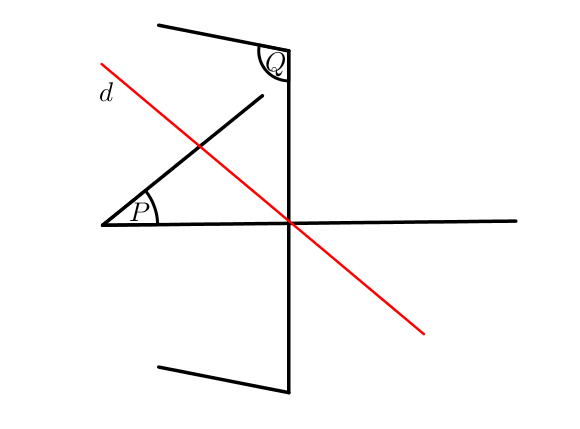
Théorème du toit
Théorème du toit
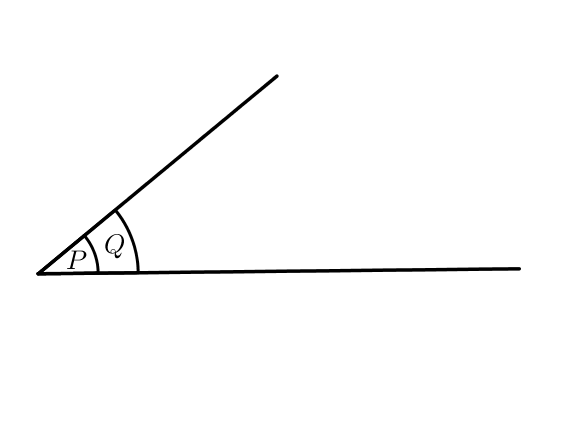
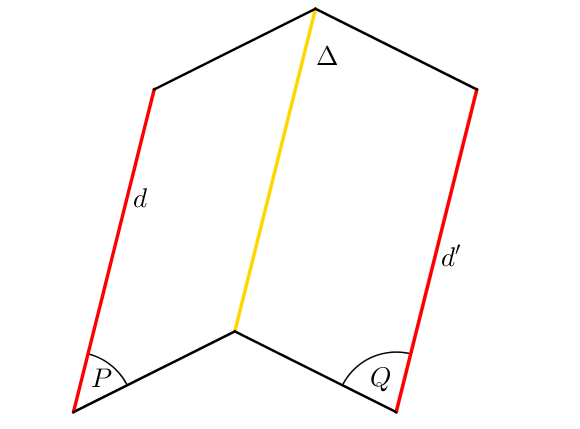
La configuration des deux plans forme un toit, ce qui explique le nom de ce théorème.
Théorème :
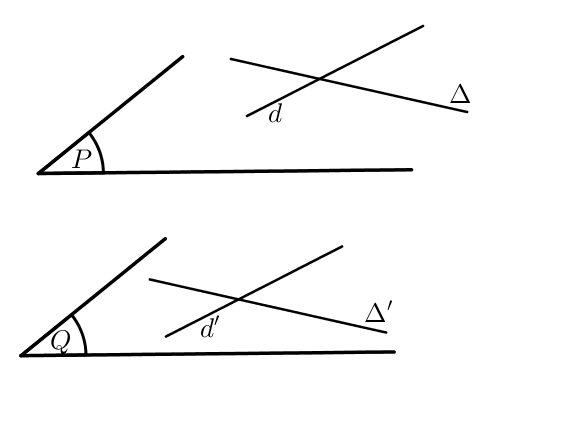
Soient $P$ et $Q$ deux plans de l’espace sécants selon la droite $\Delta$,
Soit $d$ une droite de $(P)$
$d’$ une droite de $(Q)$
Si $d\ // \ d’$ alors $d\ // \ \Delta \ // \ d’$.
Ce théorème permet de montrer que des droites sont parallèles :
Si deux droites sont parallèles dans deux plans sécants, alors ces droites sont parallèles à la droite d’intersection des deux plans.