Moyenne pondérée
Moyenne pondérée
On considère deux séries statistiques différentes et on cherche à déterminer la moyenne pondérée de ces deux séries.
Série 1
| Valeurs $x_i$ | 2 | 3 | 4 | 5 | Total |
| Effectifs | 11 | 7 | 8 | 4 | 30 |
| Fréquences en % | 37 | 23 | 27 | 13 | 100 |
Il existe deux méthodes pour calculer la moyenne pour ce type de série. Cela dépendra des attentes de l’énoncé, selon qu’il s’agisse d’effectuer les calculs à partir des effectifs ou des fréquences.
Avec les effectifs :
La moyenne est calculée avec la formule suivante :
$ \overline{x} = \dfrac{2\times 11 + 3 \times 7 + 4 \times 8 + 5 \times 4}{30}$,
Le numérateur correspond à la somme des produits des valeurs par les effectifs, et le dénominateur est égal à l’effectif total.
On trouve alors $\overline{x} \approx 3,17$.
L’interprétation et l’arrondi dépendront de l’exercice. Si il s’agissait par exemple du nombre de livres lus dans une école, on préférera arrondir à l’unité.
Avec les fréquences :
La moyenne est calculée ici avec la formule suivante :
$ \overline{x} = \dfrac{2\times 37 + 3 \times 23 + 4 \times 27 + 5 \times 13}{100}$,
Le numérateur correspond à la somme des produits des valeurs par les fréquences, et le dénominateur est égal à la fréquence total.
On trouve alors $\overline{x} \approx 3,16$.
Série 2
On s’intéresse maintenant à une série statistique regroupée par classe.
| Valeurs | $[0; 2[$ | $[2; 4[$ | $[4; 6[$ | Total |
| Effectifs | 10 | 13 | 7 | 30 |
| Centre de la classe | 1 | 3 | 5 |
Cela peut par exemple représenter le nombre de livres lu dans une école.
Ainsi, 10 élèves ont lu entre 0 et 2 livres. Cela signifie qu’en moyenne, 10 élèves ont lu 1 livre.
Le centre de la classe correspond au milieu des intervalles de valeurs.
On effectue donc le calcul suivant pour trouver la moyenne de cette série statistique :
$ \overline{x} = \dfrac{1\times 10 + 3 \times 13 + 5 \times 7}{30}$,
le numérateur correspond à la somme des produits des valeurs par les centres des classes, et le dénominateur est égal à l’effectif total.
On trouve alors $\overline{x} \approx 2,8$.
Intervalle de fluctuation
Polygone des fréquences cumulées croissantes
Polygone des fréquences cumulées croissantes
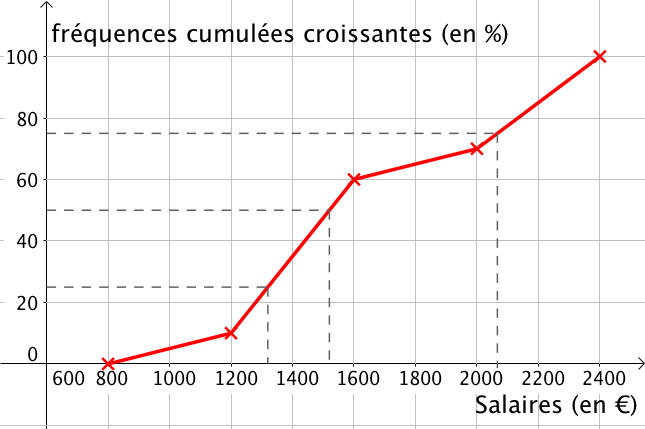
On considère le tableau des fréquences cumulées croissantes suivant et il s’agit de construire le polygone des fréquences cumulées croissantes.
| Salaires (centaines d’euros) | $[8; 12[$ | $[12; 16[$ | $[16; 20[$ | $[20; 24]$ |
| Fréquences Cumulées Croissantes | 10 | 60 | 70 | 100 |
Ce tableau signifie par exemple que 10% des employés ont un salaire compris entre 800 et 1200€.
Pour construire le polygone, on représente tout d’abord le graphique dont les axes sont les fréquences cumulées en fonction des salaires. On pourra commencer la graduation de l’axe des abscisses à partir de 800€.
Ensuite, on indique pour chaque classe la fréquence cumulée croissante. Par exemple, pour la première classe, on mettra une croix pour une abscisse de 1200 et une ordonnée de 10. Pour la seconde, on mettra une croix pour une abscisse de 1600 et une ordonnée de 60.
Une fois tous les points placés sur le graphique, on relit tous les points entre eux en rajoutant un point dont l’abscisse correspond à la plus petite valeur de salaire et ayant comme abscisse 0.
Ce graphique s’interprète par exemple sous la forme : 60% des salariés gagne moins de 1600€ par mois.
Graphiquement, il est également possible de lire la médiane de la série statistique. On se place sur l’axe des ordonnées à 50% et on trace une droite verticale. On trace ensuite une droite horizontale passant par le point d’intersection entre la droite verticale et le polygone. Graphiquement, on trouve que la médiane vaut environ 1500€.
On peut également lire graphiquement une valeur approchée des quartiles en suivant la même méthode mais en se plaçant initialement à 25% puis 75% respectivement sur l’axe des ordonnées. Ici, $Q_1 \approx 1250$€ et $Q_3 \approx 2100$ €.
Quartiles
Quartiles
Lors du calcul de la médiane, il fallait découper la série statistique en deux sous séries de même longueur.
Pour le calcul des quartiles, il faut découper la série statistique en quart.
Définition :
Le premier quartile noté $Q_1$ correspond à la plus petite valeur telle que au moins un quart des termes de la série statistique ont une valeur inférieure ou égale à $Q_1$.
Le troisième quartile noté $Q_3$ correspond à la plus petite valeur telle que au moins trois quarts des termes de la série statistique ont une valeur inférieure ou égale à $Q_3$.
Exemple :
On considère la série statistique suivante représentant le poids de sept personnes. Déterminons les quartiles de cette série.
$ 65 \ ;\ 54\ ;\ 84\ ;\ 66\ ;\ 84\ ;\ 59\ ;\ 70$
Pour obtenir les deux quartiles à partir de cette série statistique, il faut d’abord la classer par ordre croissant.
$\ 54\ ;\ 59\ ;\ 65\ ;\ 66\ ;\ 70\ ;\ 84\ ;\ 84$
Pour déterminer le premier quartile, on commence par calculer le quart de l’effectif.
Ici, l’effectif est égal à 7 : $\dfrac{1}{4} \times 7 = 1,75$.
Cela signifierait alors que le premier quartile serait le terme de rang 1,75 qui n’existe pas.
Dans ce cas là, le premier quartile est le terme dont le rang est le premier entier supérieur au résultat du calcul précédent.
Ici, le premier quartile est donc le terme de rang 2, c’est à dire
$Q_1 = 59$ kg.
Pour déterminer le troisième quartile, on commence par calculer les trois quarts de l’effectif.
Ici, $\dfrac{3}{4} \times 7 = 5,25$.
Comme précédemment, le troisième quartile est le terme dont le rang est le premier entier supérieur au résultat du calcul précédent.
Ici, le troisième quartile est donc le terme de rang 6, c’est à dire
$Q_3 = 84$ kg.