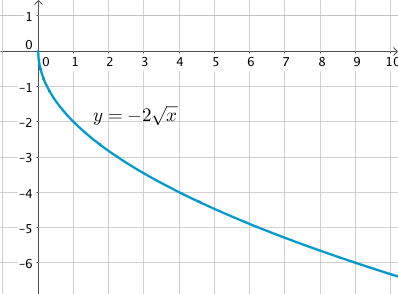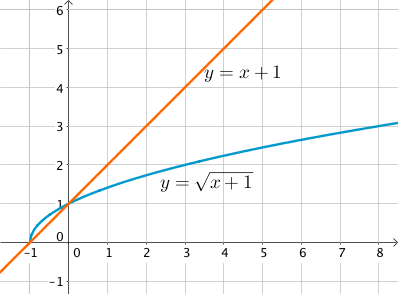Variations des fonctions associées
Variations des fonctions associées
Soit $u$ un fonction définie sur $I$, on s’intéresse aux variations de la fonction obtenue après transformation (addition, multiplication …).
1) la fonction $u + k, \ k \in \mathbb{R}$.
La fonction $u + k$ a les mêmes variations que la fonction $u$.
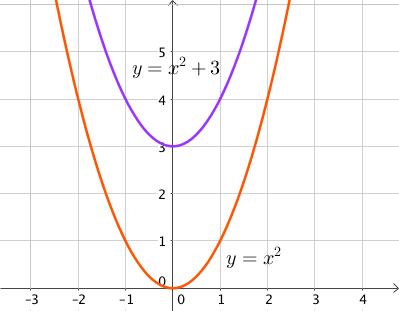
Par exemple la fonction $x^2 + 3$ a les mêmes variations que la fonction $x^2$ : elle est décroissante pour $x$ négatif et croissante pour $x$ positif.
Ainsi, ajouter $k$ à une fonction $u$ revient à translater la courbe de la fonction $u$ de $k$ unités selon l’axe des ordonnées.
2) la fonction $\lambda u, \ \lambda \in \mathbb{R}$
Si $\lambda < 0$, les variations de $\lambda u$ sont contraires à celles de $u$.
Si $\lambda > 0$, les variations de $\lambda u$ sont identiques à celles de $u$.
Par exemple, la fonction $\sqrt{x}$ est croissante sur $\mathbb{R}^+$. Ainsi, la fonction $-2\sqrt{x}$ est décroissante sur $\mathbb{R}^+$ car $-2 < 0$.
3) la fonction $\sqrt{u}$
Si $u$ est positive, alors $u$ et $\sqrt{u}$ ont le même sens de variations.
Considérons la fonction $u(x) = x + 1$ définie et croissante sur $\mathbb{R}$.
Pour pouvoir lui appliquer la fonction racine carrée, la fonction $u$ doit être positive.
Il faut donc se placer sur l’intervalle $[-1; + \infty[$.
Sur cet intervalle, les fonctions $x + 1$ et $\sqrt{x + 1}$ ont les mêmes variations : elles sont toutes deux croissantes.
4) la fonction $\dfrac{1}{u}$
Si $u$ ne change pas de signe et ne s’annule pas sur un intervalle, alors les fonctions $u$ et $\dfrac{1}{u}$ ont des sens de variations contraires.
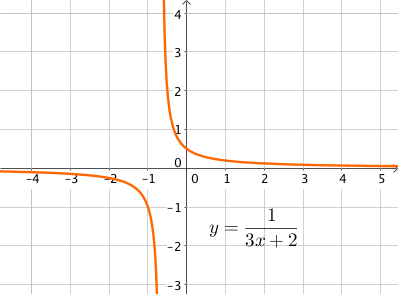
Soit par exemple la fonction $u = 3x + 2$ croissante sur $\mathbb{R}$.
Sur $]- \infty; -\dfrac{2}{3} [$, u est strictement négative et ne s’annule pas, ainsi $\dfrac{1}{3x + 2}$ est décroissante sur cet intervalle.
Sur $]-\dfrac{2}{3}; +\infty [$, u est strictement positive et ne s’annule pas, ainsi $\dfrac{1}{3x + 2}$ est décroissante sur cet intervalle.
Exemple :
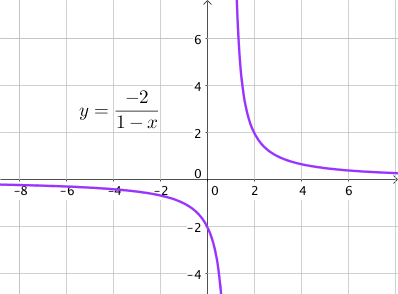
Soit $f$ la fonction définie par $f(x) = \dfrac{-2}{1 – x}$ pour tout $x \in \mathbb{R} \backslash \{1\}$.
On cherche à déterminer les variations de $f$.
On pose $u = 1 – x$ définie sur $\mathbb{R}$. $u$ est décroissante sur $\mathbb{R}$.
Or, si $u$ ne change pas de signe et ne s’annule pas sur un intervalle, alors les fonctions $u$ et $\dfrac{1}{u}$ ont des sens de variations contraires.
Ainsi, comme sur $]- \infty; 1 [$, u est strictement positive et ne s’annule pas, $\dfrac{1}{1 – x}$ est croissante sur cet intervalle.
Et, sur $]1; + \infty [$, u étant strictement négative et ne s’annulant pas, $\dfrac{1}{1 – x}$ est croissante sur cet intervalle.
Or, $f(x) = -2 \times \dfrac{1}{u}$.
En outre, si $\lambda < 0$, les variations de $\lambda u$ sont contraires à celles de $u$.
Ainsi $f$ est décroissante sur $]- \infty; 1 [$ et sur $]1; + \infty [$.