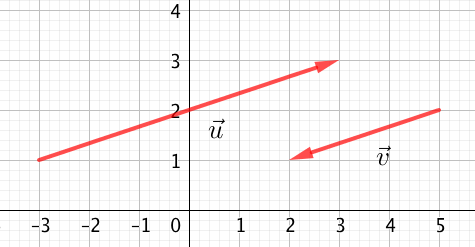Colinéarité de vecteurs

Vecteurs colinéaires

Vecteurs colinéaires

Définition

Soient $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs,

$\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si il existe un réel $k$ tel que $\overrightarrow{v} = k \overrightarrow{u}$.

(Dans ce cas, $\overrightarrow{u}=-2\times \overrightarrow{v}$ et le réel $k$ vaut $-2$)

Des vecteurs colinéaires sont portés par des droites parallèles : ils ont donc la même direction mais pas forcément le même sens. 

La colinéarité se voit sur un graphique avec la pente des vecteurs, même si cela ne constitue pas une preuve. 

Critère de colinéarité (dans un repère)

Soit un repère $(O, \overrightarrow{i}, \overrightarrow{j})$,

Soient deux vecteurs $\overrightarrow{u} \left ( \begin{array}{c} x \\y \\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x’ \\ y’ \\ \end{array} \right )$,

$\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si $x\times y’ – y \times x’ = 0$. 

Cela revient à dire que les coordonnées des vecteurs sont proportionnelles. 

Considérons $\overrightarrow{u} \left ( \begin{array}{c} 3 \\ 2\\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} 9 \\ 6 \\ \end{array} \right )$, il apparait que $\overrightarrow{v} = 3 \overrightarrow{u}$.

D’après la définition, ces deux vecteurs sont colinéaires. 

Si on applique le critère de colinéarité, on trouve $3\times 6 – 2 \times 9 = 18 – 18 = 0$ : les deux vecteurs sont colinéaires.