Interaction coulombienne et électrisation
Interaction coulombienne et électrisation
Quel est l’énoncé de la loi de Coulomb ?
La loi de Coulomb est une loi qui régit un phénomène bien connu, à savoir que deux charges « + » se repoussent, deux charges « – » se repoussent et une charge « + » et une charge « – » s’attirent. À partir de cette loi de Coulomb, on peut expliquer deux choses : le phénomène d’électrisation et le phénomène de cohésion des cristaux ioniques.
Soient deux charges ponctuelles A et B de charge \(q_A\) et \(q_B\) ( C ).
I – Cas 1 : charges opposées
Si $q_A$ est positif, $q_B$ est négatif ou inversement. Ici, on prend $q_A>0$ et $q_B<0$. Une charge positive et une charge négative s’attirent, on va déterminer quelles sont les forces exercées ici par $A$ sur $B$ et par $B$ sur $A.$
La force exercée par $B$ sur $A$ ainsi que celle exercée par $A$ sur $B$ sont représentées de la manière suivante :
On peut très facilement déterminer le point d’application, la direction et le sens. En intensité, la force exercée par $B$ sur $A$ vaut celle exercée par $A$ sur $B$.
On a alors la formule : $F_{B/A}= F_{A/B}= \dfrac{k|q_A q_B|}{r^2}$, avec $k$ une constante qui vaut $9,00.10^9 \ SI.$
On ne doit pas connaître par cœur cette constante car elle est donnée quand il faut utiliser cette loi. Attention à la valeur absolue qui est là car la norme d’une force est toujours positive donc on enlève les signes éventuels des charges. $r$ est la distance qui sépare le corps $A$ du corps $B.$ Au niveau des unités, la valeur d’une force est exprimée en newton (N), les charges sont exprimées en coulomb (C) et la distance $r$ doit être exprimée en mètres pour que le calcul soit correct.
II – Cas 2 : charges de même signe
Les charges de même signe se repoussent. On va représenter la force exercée par $A$ sur $B$ et celle exercée par $B$ sur $A$ ci-dessous :
III – Électrisation
Qu’est-ce que l’électrisation ?
Cette loi permet d’expliquer le phénomène d’électrisation. L’électrisation c’est lorsqu’on fait apparaître des charges sur un corps, de manière temporaire puisque ces charges vont ensuite disparaître.
La première manière de faire apparaître ces charges est de les faire apparaître par frottements. On prend, par exemple, une tige en PVC que l’on frotte avec un tissu en laine. Ainsi, on va arracher des électrons à la laine. Les électrons arrachés vont arriver sur la tige en PVC, celle-ci a donc un excès d’électrons et va être chargée négativement. La laine qui a perdu des électrons va être chargée positivement.
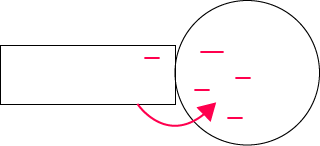
La deuxième manière d’électriser un corps est par contact. On a un conducteur mis en contact avec un tube en PVC électrisé négativement. Effectivement, les électrons vont passer du tube en PVC au conducteur juste à côté. On a l’apparition de charges négatives, ici, au niveau du conducteur. Ces charges ne viennent pas de nulle part, à chaque fois qu’une charge apparaît sur le conducteur, une charge disparaît sur le PVC.
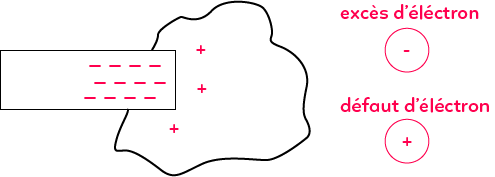
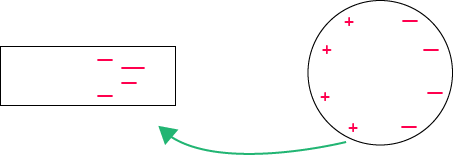
La troisième et dernière manière d’électriser un corps est par influence. On reprend le tube en PVC chargé négativement et on approche un conducteur. Des charges positives vont se mettre du côté du tube en PVC et des charges négatives vont se mettre du côté opposé au PVC. En effet, les charges négatives vont chercher à s’éloigner du tube chargé négativement et les charges positives vont chercher à s’approcher du tube chargé négativement. Ainsi, l’objet va s’approcher du tube en PVC.
Analogie entre la loi de Coulomb et la loi d’interaction gravitationnelle
Analogie entre la loi de Coulomb et la loi d’interaction gravitationnelle
I – Loi de Coulomb
Comment peut-on calculer la force subie par une particule chargée dans la loi de Coulomb ?
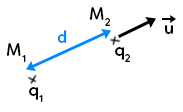
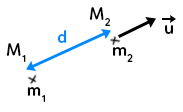
Une particule chargée $q_1$ est placée en $M_1$ et une seconde particule $q_2$ est placée en $M_2.$ Les deux particules sont séparées à une distance $d.$ On place le vecteur unitaire $\overrightarrow{u}$ dont la norme vaut 1.
La force de $M_1$ subie par $M_2$ s’écrit :
$\overrightarrow{F}_{M_1/M_2} = k \times \dfrac{q_1 \times q_2}{d^2}\times \overrightarrow{u}$
avec $k = 9.0\times 10^{9} N.m^{2}.C^{-2}$
Remarque : $\overrightarrow{F}_{M_1/M_2}$ est dans le sens de $\overrightarrow{u}$. Cela est logique car si les particules sont de même charge alors elles se repoussent.
II – Loi d’interaction gravitationnelle
Quelle est la formule de la loi d’interaction gravitationnelle entre deux masses ?
La loi d’interaction gravitationnelle permet de calculer la force subie par une masse, due à une autre. On se place dans une situation similaire, avec cette fois-ci $M_1$ et $M_2$ caractérisés par leur masse. La force de $M_1$ sur $M_2$ s’écrit alors :
$\overrightarrow{F}_{M_1/M_2} = – G \times \dfrac{m_1\times m_2}{d^2} \times \overrightarrow{u}$
avec $G = 6.67\times 10^{-11} N.m^{2}.kg^{-2}$
Remarque : $\overrightarrow{F}_{M_1/M_2}$ est une force attractive, ce qui explique le signe négatif. La force est donc dans le sens opposé à celui de $\overrightarrow{u}$.
III – Analogies
On observe une structure unitaire commune qui est le vecteur $\overrightarrow{u}$. La première analogie est que $q_1$ correspond à $m_1$ et $q_2$ correspond à $m_2.$ Ce sont également des forces en $\dfrac{1}{d^{2}}$.
Exemple : si l’on déplace une particule deux fois plus loin de masse $m$ et de charge $q $données, la force sera quatre fois plus faible.
On peut comparer $k$ et $- G$ pour chacune des lois. On peut également remarquer que les deux lois s’inscrivent dans un champ : le champ électrostatique $\overrightarrow{E}$ pour la loi de Coulomb et le champ gravitationnel $\overrightarrow{G}$ pour la loi d’interaction gravitationnelle.
Enfin, pour la loi de Coulomb on utilise $\overrightarrow{E}$ pour calculer la force subie par une particule chargée $q.$
$\overrightarrow{F} = q\times \overrightarrow{E}$
Dans le cadre de la loi d’interaction gravitationnelle, on utilise $\overrightarrow{G}$ pour calculer la force subie par une particule de masse $m.$
$\overrightarrow{F} = m\times \overrightarrow{G}$