Généralités sur les champs
On verra ici ce qu’est un champ en physique et on verra plus tard ce qu’est un champ magnétique et un champ de pesanteur.
Grandeurs physiques
Les grandeurs physiques sont des grandeurs mesurées. Dans ces grandeurs physiques, il y a les grandeurs scalaires et les grandeurs vectorielles.
Une grandeur scalaire est totalement définie par sa valeur. Par exemple, la température. Si on dit « il fait 20°C » la valeur 20 et l’unité degrés Celsius définissent entièrement la grandeur physique scalaire « température ».
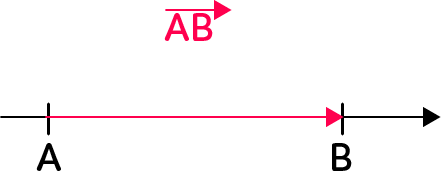
Il existe aussi des grandeurs vectorielles. Elles sont définies entièrement par le vecteur, c’est-à-dire un point d’application, une direction, un sens et une valeur. Un petit rappel sur les vecteurs :
On a le vecteur AB donc le point d’application serait A. La direction est la droite (AB) ou horizontale. Le sens est A vers B. Attention à ne pas confondre direction et sens, c’est une confusion faite régulièrement. Et la norme ou valeur (ou intensité) est la longueur AB.
Champs scalaires
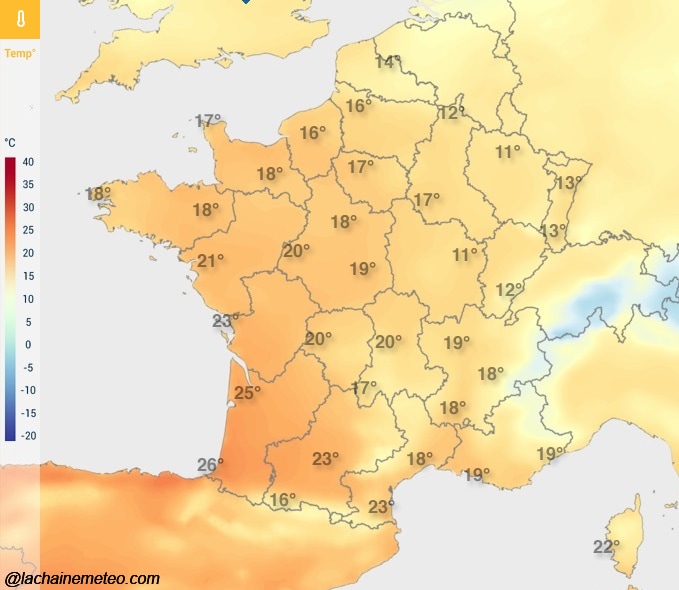
C’est l’ensemble des valeurs prises par une grandeur physique scalaire dans l’espace. Un exemple classique de champ scalaire est le champ de température.
On détaille, à chaque endroit de la France, quelle est la température pour une matinée ou une après-midi. Donc, sur les champs scalaires on a les équipotentielles. Ce sont des courbes qui relient les mêmes valeurs. Par exemple, on relie les endroits en France où il fait 18°C. On parle de champs uniformes si l’ensemble des valeurs de cette grandeur scalaire sont les mêmes. Par exemple, s’il fait 18°C sur l’ensemble de la France, ce sera un champ scalaire de température uniforme.
Champs vectoriels
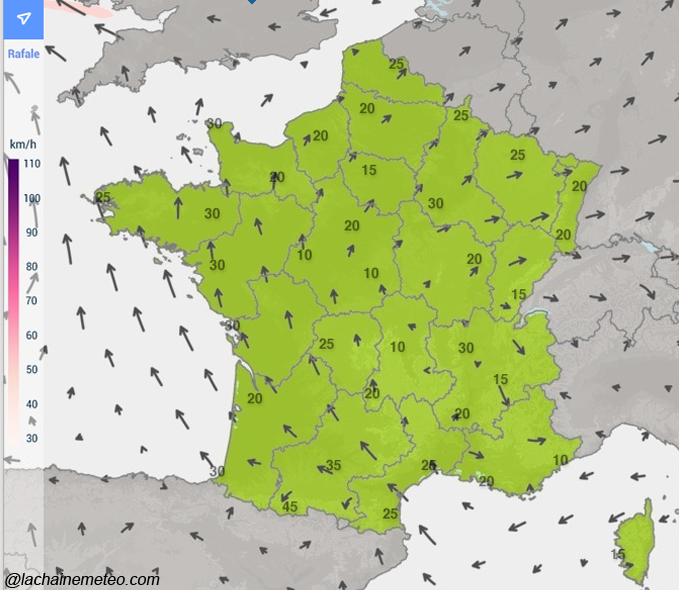
C’est l’ensemble des vecteurs dans l’espace. Par exemple, l’ensemble des vitesses des vents sur une région ou sur la France.
On indique par les petites flèches (par les vecteurs) la direction, le sens et l’intensité des vents selon sa localisation dans l’espace. On parle, dans le cas des champs vectoriels, des lignes de champs. Ce sont les lignes qui sont tangentes aux vecteurs.
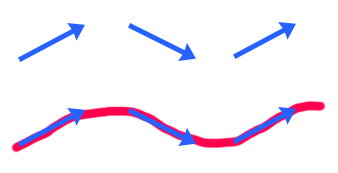
La ligne de champs est la courbe qui rejoint ces trois vecteurs, on l’oriente dans le sens général, ici, des trois vecteurs. A l’inverse, si l’on a une ligne de champs et que l’on doit déterminer le vecteur en une position de l’espace, il suffit de prendre la tangente à la ligne de champs dans l’espace au point considéré. On parle de champ uniforme, un peu comme avec les champs scalaires, lorsqu’on aura des lignes de champs qui seront parallèles entre-elles.
Le champ électrostatique
Sources
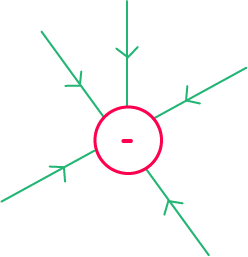
Les sources de champs électrostatique sont les entités chargées électriquement. C’est-à-dire qu’une charge positive dans l’espace crée un champ électrostatique tout comme les charges négatives. On a ici les lignes de champ créées par une charge positive et par une charge négative :
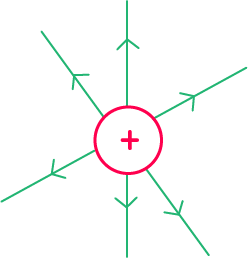
Les lignes de champ s’éloignent de la charge positive et les lignes de champ se rapprochent de la charge négative.
Détection
Pour détecter un champ électrostatique on utilise également des entités chargées électriquement. Une entité chargée électriquement dans un champ électrostatique subit une force et est déviée de sa trajectoire. Cette force est la force électrostatique notée $\overrightarrow{F},$ c’est un vecteur.
Notation et caractéristiques
On note le champ électrostatique $\overrightarrow{E},$ avec une flèche car c’est un champ vectoriel. Puisque c’est un champ vectoriel on le caractérise par une direction, un sens et une norme, valeur ou intensité. La direction du champ électrostatique est celle des lignes de champ mais aussi celle de la force que subit la particule chargée électriquement qui caractérise ce champ électrostatique.
On a la relation : $\overrightarrow{E} =\dfrac{\overrightarrow{F}}{q}$
$\overrightarrow{E}$ est le champ électrostatique, $\overrightarrow{F}$ est la force électrostatique ressentie par la particule chargée électriquement de charge $q$ exprimée en Coulomb.
La direction du champ et de la force ressentie par la particule est la même.
Pour le sens, cela dépend si la particule qui sert à détecter est chargée positivement ou négativement. Si la particule qui sert à détecter est chargée positivement et qu’on a une charge électrostatique dans le sens gauche vers la droite, le champ $\overrightarrow{E}$ va être dans le même sens. Si on a une particule chargée négativement, le champ $\overrightarrow{E}$ va être dans le sens inverse de la force ressentie.
Pour la norme ou valeur du champ électrostatique, on a : $E = \dfrac{F}{|q|}$, en valeur absolue puisqu’on a une valeur positive pour la norme. Au niveau des unités, une force est exprimée en $N,$ une charge en $C$ donc le champ sera exprimé en $N.C^{-1},$ on utilise aussi les unités $V.m^{-1}.$ Ces deux unités sont équivalentes.
Champ uniforme
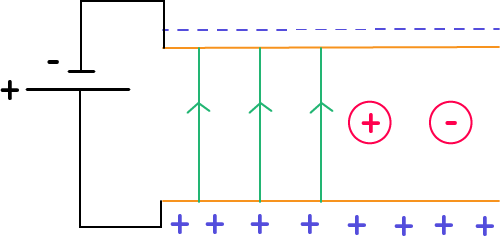
Pour obtenir un champ uniforme, on utilise un condensateur plan.
Le condensateur est un objet constitué de deux armatures reliées à une pile, un générateur. Ces deux armatures sont chargées différemment, on a une charge « – » du côté de la borne « – » et une charge « + » du côté de la borne « + ». Entre ces deux armatures, il y a un isolant et à l’intérieur du condensateur plan on a des lignes de champ qui sont des droites parallèles. On a un champ électrostatique uniforme. Si on a une charge positive à l’intérieur de ce champ électrostatique uniforme, avec le champ $\overrightarrow{E}$ vers le haut qui suit les lignes de champ, d’après la formule, la charge positive va subir une force électrostatique orientée dans le même sens que le champ, donc la charge positive va vers l’armature du condensateur chargée négativement. Si on place une charge négative dans le champ électrostatique créé par le condensateur plan, cette charge négative va dans le sens opposé à celui du champ électrostatique. La force électrostatique est dans le sens opposé au champ électrostatique et donc on a la charge négative qui va vers l’armature métallique chargée positivement du condensateur.
Par exemple sur cette photographie, on peut observer les lignes de champ électrostatique en plaçant un liquide isolant avec de petites graines.
Champ gravitationnel et électrostatique
Champ gravitationnel et électrostatique
I. Définition
Un champ est une grandeur physique qui a une valeur en tout point de l’espace. Il existe deux types de champ : les champs scalaires et les champs vectoriels.
Exemples
On peut créer une cartographie de la température à tout point dans l’espace (champ de température, scalaire). Le champ gravitationnel est vectoriel car il possède une direction et un sens.
II. Champ gravitationnel $\overrightarrow{\cal{G}}$
Le champ a une utilité en physique : il permet de calculer la force subie par une masse $m$ que l’on mettrait en un point $M.$ On peut, en théorie, cartographier le champ gravitationnel en tout point de l’espace. On a :
$\overrightarrow{F}_{M} = m\times \overrightarrow{\cal{G}}_{M}$
$F$ et $\cal{G}$ sont de même sens. Le champ gravitationnel est radial et vers le centre de la Terre dans un référentiel géocentrique et vertical vers le bas dans un référentiel terrestre (localement sur Terre). On parle de lignes de champ sur Terre.
III. Champ électrique $\overrightarrow{E}$
Le champ électrique permet de calculer la force subie par une charge $q$ que l’on placerait en un point de l’espace appelé $M.$ On a alors :
$\overrightarrow{F}_{M} = q\times \overrightarrow{E}_{M}$
Remarque : Les vecteurs $\overrightarrow{F}$ et $\overrightarrow{E}$ sont colinéaires peu importe le signe de $q.$
Si $q > 0$, $\overrightarrow{F}$ et $\overrightarrow{E}$ sont de même sens.
Si $q < 0$, $\overrightarrow{F}$ et $\overrightarrow{E}$ sont de sens opposés.
Dans le cas d’un proton, on a une particule chargée positivement. Les particules chargées positivement se repoussent et on va donc avoir une force allant dans une direction opposée à l’endroit où est localisé le proton.
Si l’on place au centre une particule chargée négativement, comme un électron, les particules positives vont être attirées vers le centre, où se situe l’électron. Elles subissent une force attractive.
On se place maintenant dans le cas d’un condensateur : un condensateur est constitué de deux plaques se faisant face et séparées par un isolant, à travers lequel le courant ne peut pas circuler. Les électrons vont donc se charger et chacun être associés à un défaut d’électron. Il va ainsi y avoir un champ électrique entre ces deux plaques.
Si l’on place une particule positive entre les deux plaques, elle va être attirée par les électrons chargés négativement. On peut également calculer la valeur du champ électrique avec :
$E = \dfrac{U}{d}$
Avec $U$ la différence de potentiel entre les deux plaques en $V$ et $d$ la distance entre les deux plaques en $m.$