Vecteur directeur d'une droite, équation cartésienne
Vecteur directeur d’une droite, équation cartésienne
I) Définition
Soit $(\mathcal{D})$ une droite du plan,
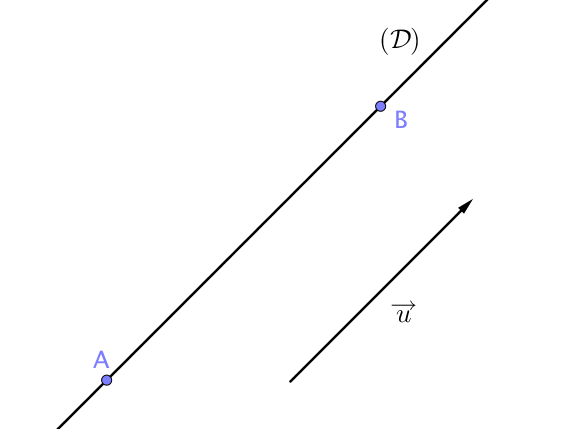
on appelle vecteur directeur de $(\mathcal{D})$ tout vecteur non nul $\overrightarrow{u}$ qui possède la même direction que la droite $(\mathcal{D})$.
Si l’on connait deux points $A$ et $B$ de la droite, alors le vecteur $\overrightarrow{AB}$ est un vecteur directeur de cette dernière.
Comme le choix de $A$ et $B$ appartenants à le droite est arbitraire, il existe une infinité de vecteurs directeurs.
Tous ces vecteurs directeurs ont la même direction, celle de $(\mathcal{D})$, ils sont donc colinéaires.
Exemple :
On se place dans un repère.
On appelle $(\mathcal{d})$ la droite passant par les points $A(2;1)$ et $B(1;3)$. On souhaite donner les coordonnées d’un vecteur directeur de la droite $(\mathcal{d})$.
D’après la propriété précédente, on sait que le vecteur $\overrightarrow{AB}$ est un vecteur directeur de la droite, il ne reste donc qu’à calculer ses coordonnées.
$\overrightarrow{AB}(x_B – x_A; y_B – y_A)$
Donc $\overrightarrow{BA}(1 – 2; 3 – 1)$.
Finalement, un vecteur directeur de $(\mathcal{d})$ est $\overrightarrow{AB}(-1; 2)$.
II ) Equation cartésienne d’une droite
Définition
Toute droite $(\mathcal{D})$ admet une équation de la forme $ax + by + c = 0$ avec $(a, b) \neq (0, 0)$.
Cette équation est appelée équation cartésienne de la droite $(\mathcal{D})$.
Théorème
Un vecteur directeur de $(\mathcal{D})$ est $\overrightarrow{u}(-b; a)$.
Démonstration
Soit $A(x_A; y_B)$ un point de la droite $(\mathcal{D})$ et $\overrightarrow{u}(\alpha; \beta)$ un vecteur directeur de la droite $(\mathcal{D})$.
Soit $M$ un point du plan de coordonnées $M(x; y)$,
$M(x; y) \in (\mathcal{D}) $ si et seulement si les vecteurs $\overrightarrow{AM}(x_M – x_A; y_M – y_A)$ et $\overrightarrow{u}(\alpha; \beta)$ sont colinéaires
si et seulement si det($\overrightarrow{AM}, \overrightarrow{u}) = \left| \begin{array}{cc} x – x_a & \alpha \\ y – y_a & \beta \end{array} \right| = 0$
si et seulement $ (x – x_a)\beta – (y – y_a)\alpha = 0$
si et seulement si $\beta x – \alpha y + \alpha y_a – \beta x_a = 0$.
Cette équation peut donc s’écrire $ax + by + c = 0$ avec $\left \{ \begin{array}{l} a = \beta \\ b = – \alpha \\ c = \alpha y_a – \beta x_a \end{array} \right.$
Le vecteur directeur est donc $\overrightarrow{u}(\alpha; \beta) = \overrightarrow{u}(-b; a)$.