Relativité du mouvement
I. Le référentiel
Il est important de d’abord définir le référentiel pour pouvoir parler de relativité. Le référentiel sert à étudier le mouvement d’un corps. C’est le point de vue que l’on choisit pour étudier le mouvement d’un corps.
Le référentiel terrestre
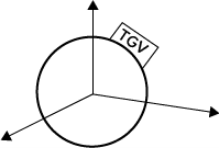
Le référentiel terrestre est la surface de la Terre ou tout autre objet fixe par rapport à la Terre.
On voit dans le référentiel terrestre un TGV passer selon une ligne droite (sur les rails).
Le référentiel géocentrique
Le référentiel géocentrique est défini par le centre de la Terre et ses axes sont fixes.
Dans ce référentiel, la Terre tourne, et le TGV tourne autour de la Terre.
Le référentiel héliocentrique
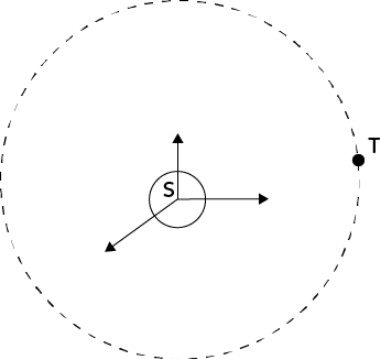
Le référentiel héliocentrique est défini par le centre du soleil et ses axes sont fixes.
Dans ce référentiel, la Terre tourne sur elle-même mais tourne aussi autour du soleil.
II. Relativité
Il a deux types de relativité : la relativité de la vitesse ou de la trajectoire.
Vitesse
La vitesse d’un point en mouvement dépend du référentiel dans lequel est étudié le mouvement. Par exemple : Le mouvement d’un train dans le référentiel terrestre et géocentrique. Dans le référentiel terrestre, la vitesse du TGV est de 300 km/h en ligne droite. Par contre dans le référentiel géocentrique, la vitesse du train n’est pas de 300 km/h, car la surface de la Terre tourne aussi. Donc la vitesse du train est sa vitesse à lui (300 km/h) plus la vitesse de la surface de la Terre.
Trajectoire
Trajectoire : ligne formée par l’ensemble des positions occupées par un point matériel au cours de son mouvement. La trajectoire dépend elle aussi du référentiel choisi. Par exemple : dans le référentiel terrestre le TGV va en ligne droite mais la dans le référentiel géocentrique celui-ci a une trajectoire en arc de cercle.
La trajectoire d'un point
I. Définition
La trajectoire du point est la courbe formée par les positions successives de ce point. Cela peut former différents types de courbes.
II. Quelques trajectoires à connaître
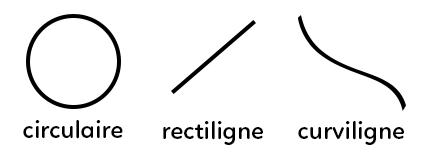
Il a trois grands types de trajectoire à connaître :
– la trajectoire circulaire (un rond),
– la trajectoire rectiligne (une ligne droite),
– la trajectoire curviligne (on ne peut pas décrire précisément la forme géométrique).
III. Comment repérer la position ?
On peut repérer la position à chaque instant d’un point M :
Repérer la position d’un point revient à créer une grandeur qui sert à savoir où se trouve le point à un instant donné. Cela revient à créer un repère (x,y), et chaque point a des coordonnées : une abscisse x et une ordonnée y. En connaissant les coordonnées de ce point, on connait la position. Il reste à connaître le moment qui correspond à cette position : il faut une horloge.
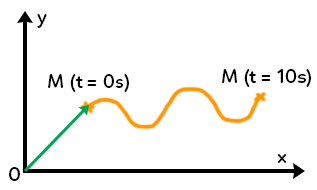
Définition : vecteur position $\overrightarrow{OM}$ = il caractérise la position du point, c’est une flèche qui va de $O$ jusqu’au point $M.$ Ce vecteur varie au cours du temps : le vecteur $\overrightarrow{OM}(t=0s)$ est différent du vecteur $\overrightarrow{OM}(t=10s)$.
IV. Mouvement uniforme, accéléré ou ralenti
Ce sont des informations qui caractérisent la vitesse du point $M.$ En résumé :
– Si la norme du vecteur vitesse est constante le long d’une trajectoire : on parle d’un mouvement uniforme.
– Si la norme du vecteur vitesse augmente le long d’une trajectoire : on parle d’un mouvement accéléré.
– Si la norme du vecteur vitesse diminue le long d’une trajectoire : on parle d’un mouvement ralenti.