Propagation et vitesse des ondes
Propagation et vitesse des ondes
I. Les ondes sonores
Les ondes sonores se propagent dans un milieu matériel à une vitesse $v$ : en effet les ondes sonores sont la vibration du milieu matériel (les ondes sonores ne se propagent donc pas dans le vide).
Par exemple, dans l’air à 20°C, la vitesse d’une onde sonore est de $v \simeq 340 \ m.s^{-1} $ (ou 340 m/s).
La relation fondamentale à connaître est :
$v=\dfrac{d}{t}$
où $v$ est la vitesse de l’onde (en m/s), $d$ la distance parcourue (en m) par l’onde et $t$ le temps du parcours (en s).
Exemple
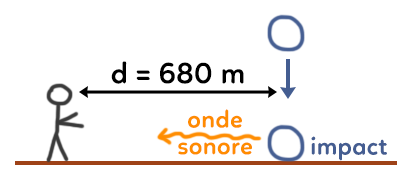
Imaginons un objet tombant sur le sol. A l’instant de l’impact, une onde sonore va être émise. La personne qui va entendre le son est à 680 m de l’impact. Combien de temps faut-il pour que l’onde sonore atteigne la personne ?
On utilise alors la relation fondamentale en isolant le temps $t$ : $t=\dfrac{d}{v}=\dfrac{680}{340}=2 \ s$
Il faut donc un certain laps de temps pour que la personne entende l’onde sonore : ce n’est pas instantané.
II. Les ondes lumineuses
Les ondes lumineuses se propagent dans le vide ou tout autre milieu transparent (en effet on reçoit bien les rayons du Soleil, alors que ceux-ci doivent traverser le vide entre la Soleil et la Terre).
La relation fondamentale se conserve mais la vitesse des ondes lumineuses est $v=3,00 \times 10^8 \ m/s$.
Cette vitesse est bien plus rapide que la vitesse des ondes sonores.
Les ondes sonores
Les ondes sonores
I. Vitesse de propagation
L’onde sonore est un son qui se propage. Par exemple, un haut-parleur avec du son qui se propage vers l’avant à une certaine vitesse. La vitesse du son dans l’air correspond à 340 m/s, pour une température de 15 °C. Dans l’eau, le son va plus vite. Si dans un tableau on donne des valeurs, on doit pouvoir comparer la vitesse du son dans l’eau avec la valeur de la vitesse du son dans l’air.
II. Fréquences audibles par l’homme
Un son, pour qu’il soit perceptible par l’oreille humaine, doit être compris entre deux fréquences : 20 Hz et 20 kHz.
S’il est hors de ces bornes, le son existe mais on ne l’entend pas. Ce sont les ultrasons par exemple. Les chauve-souris se déplacent grâce à des émissions d’ultrasons. On ne les entend pas mais pourtant ils existent.
III. La hauteur d’un son
Plus communément on dit : aigu ou grave ? Pour connaître cette notion, on va devoir avoir une information sur sa fréquence.
Si un son est à haute fréquence, il est aigu.
Si un son est à basse fréquence, il est grave.
Cela n’est pas quelque chose d’absolu. En général, on s’en sert pour comparer deux sons et pour savoir quel son est plus aigu/grave que l’autre.
Comment trouver la fréquence ?
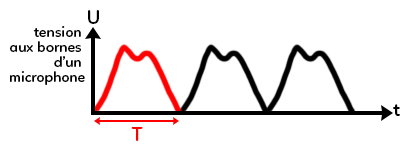
Parfois c’est donné dans l’énoncé, parfois on donne la tension mesurée aux bornes d’un microphone (qui permet d’enregistrer un son). La tension évolue au cours du temps, par exemple, de cette façon :
La première information que l’on peut soutirer est la période du signal. On a alors un signal périodique et il faut repérer l’élément qui se répète. Ici, on voit que l’élément en rouge se répète. La durée entre le début du motif rouge et le début du motif blanc s’appelle la période. Elle est notée $T.$
$T$ est un temps donc on peut le mesurer. Ici, on ne peut pas car il n’y a pas d’échelle mais dans les exercices, il y aura une échelle.
Ensuite, pour avoir la fréquence, on utilise la formule :
$f = \dfrac{1}{T}$.
Par exemple, si $T = 10 \ ms.$ L’unité du temps étant la seconde, on va devoir convertir cette valeur en seconde. On divise par $1000,$ on obtient $0,01 \ s.$
On utilise la formule : $f = \dfrac{1}{0,01} = 100 \ Hz$.
Est-ce un son plutôt grave ou aigu ? Puisque l’intervalle audible est entre 20 et 20 000 Hz, 100 Hz est plus proche des sons les plus bas audibles par l’oreille humaine donc c’est un son plutôt grave. Mais tout est relatif ! Si on arrive à émettre un son à 50 Hz, alors il sera encore plus grave que celui-là.
IV. Niveau d’intensité sonore
Les formules ne sont pas au programme en Seconde et donc ne sont pas à connaître pour cette partie. Ce qui permet de mesurer le niveau d’intensité sonore c’est un sonomètre. Le sonomètre indique cette valeur en décibels (dB).
Plus le son est fort, plus la valeur en dB du niveau d’intensité sonore est importante.
Il ne faut pas confondre niveau d’intensité sonore et intensité sonore. L’intensité sonore est une autre grandeur en relation avec la puissance sonore du son. Elle s’exprime en W.m2. Si l’intensité sonore augmente, le niveau d’intensité sonore augmente aussi.