Volumes de pavés et changement d’unités
Volumes de pavés, changement d’unités
Volume d’un parallélépipède rectangle ou Pavé droit
Le volume d’un solide est la partie remplissant l’intérieur du solide. L’unité principale de mesure du volume est le $m^3$.
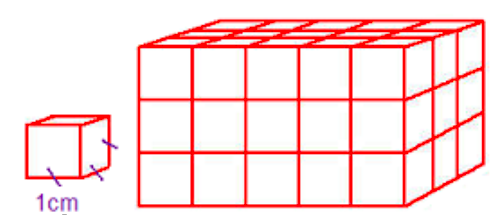
On utilise aussi d’autres unités : dans cet exemple, le volume du pavé est :
$V=5\times 3\times 3 = 45 cm^3$ (Le petit cube rouge a un volume de $1cm^3$ et le pavé est composé de $45$ petits cubes identiques)
Formule du volume d’un pavé droit
$V=l\times L\times H$
à retenir : $V= Longueur\times largeur\times hauteur$
Exemple :
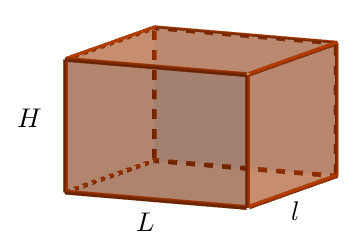
Dans la figure ci-contre, on choisit :
$L=3m, l=1,5m$ et $H = 1,2m$
On a : $V = 3\times 1,5\times 1,2$
$V = 5,4 m^3$
Unités de volumes
Pour calculer le volume, on multiplie 3 grandeurs : la longueur, la largeur et la hauteur.
C’est pour cela que l’unité de volume est le $m^3$ (on dit “mètre cube”).
Pour mesurer les capacités, on utilise : Le litre et ses unités associées.
À retenir : $1 L= 1 dm^3$