Suites arithmétiques - Définition
Suites arithmétiques
Définition
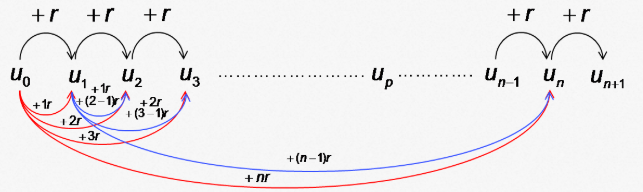
Une suite arithmétique est une suite pour laquelle chaque terme permet de déduire le suivant en lui ajoutant le même nombre : la raison $r$.
Pour définir une suite arithmétique $(u_n)_{(n \in \mathbb{N})}$, il faut un premier terme, $u_0$ généralement, et la raison $r$ ($r \in \mathbb{R}$).
On écrit alors : $\left \{ \begin{array}{l} u_{n + 1} = u_n + r \\ u_0 \\ \end{array} \right.$
Exemple :
Considérons la suite $\left \{ \begin{array}{l} u_{n + 1} = u_n – 7 \\ u_0 = 17 \\ \end{array} \right.$.
On obtient donc $u_1 = 17 – 7 = 10$ et $u_2 = 10 – 7 = 3$.
Cette définition par récurrence ne permet cependant pas de trouver directement n’importe quel terme de la suite : il faut avoir calculé tous les termes précédents.
Il existe néanmoins une formule générale, dite explicite, qui permet de calculer n’importe quel terme de la suite.
Propriétés
Pour tout $n \in \mathbb{N}$ $u_n = u_0 + nr$.
En effet, pour passer de $u_0$ à $u_n$ il faut ajouter $n$ fois la raison.
Si le terme donné de la suite n’est pas $u_0$, la formule plus générale est la suivante :
pour tous $n, \ p \in \mathbb{N}, \ u_n = u_p + (n – p)r$.
En reprenant l’exemple précédent, on peut déterminer $u_7 = u_0 + 7 \times (-7) = -32$
Comment montrer qu'une suite est arithmétique ?
Comment montrer qu’une suite est arithmétique ?
La seule méthode pour montrer qu’une suite $(u_n)$ est arithmétique consiste à étudier la différence entre le terme $(n + 1)^{\text{ème}}$ de la suite et le $n^{\text{ème}}$ pour tout $n \in \mathbb{N}$ ou encore à étudier la différence : $u_{n + 1} – u_n$.
Si le résultat de cette différence est une constante, la suite est arithmétique, sinon elle ne l’est pas.
Considérons l’exemple suivant : $u_n = 3n – 8$ pour $n \in \mathbb{N}$.
On étudie donc :
$\begin{aligned}u_{n + 1} – u_n &=& 3(n + 1) – 8 – (3n – 8) \\ &=& 3n + 3 – 8 – 3n + 8 \\ &=& 3 \end{aligned}$
Ainsi, $u_{n + 1} – u_n = 3$, la différence est donc une constante donc $(u_n)$ est une suite arithmétique de raison $3$ et de premier terme $u_0 = 3\times 0 – 8 = -8$.
Considérons à présent l’exemple suivant : $u_n = n^2 – 1$ pour $n \in \mathbb{N}$.
On étudie donc :
$\begin{aligned}u_{n + 1} – u_n &=& (n + 1)^2 – 1 – (n^2 – 1) \\ &=& n^2+2n+1-1-n^2+1 \\ &=& 2n+1 \end{aligned}$
Ainsi, $u_{n + 1} – u_n = 2n+1$, la différence n’est donc pas une constante puisque ce résultat dépend de $n$ donc $(u_n)$ n’est pas une suite arithmétique .