Théorème des valeurs intermédiaires
Théorème des valeurs intermédiaires
Théorème
Soient $f$ une fonction continue sur un intervalle $I$ et $a$ et $b$ deux réels dans l’intervalle $I$ tels que $a\leqslant b $.
Alors, pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe au moins un réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
Illustration graphique
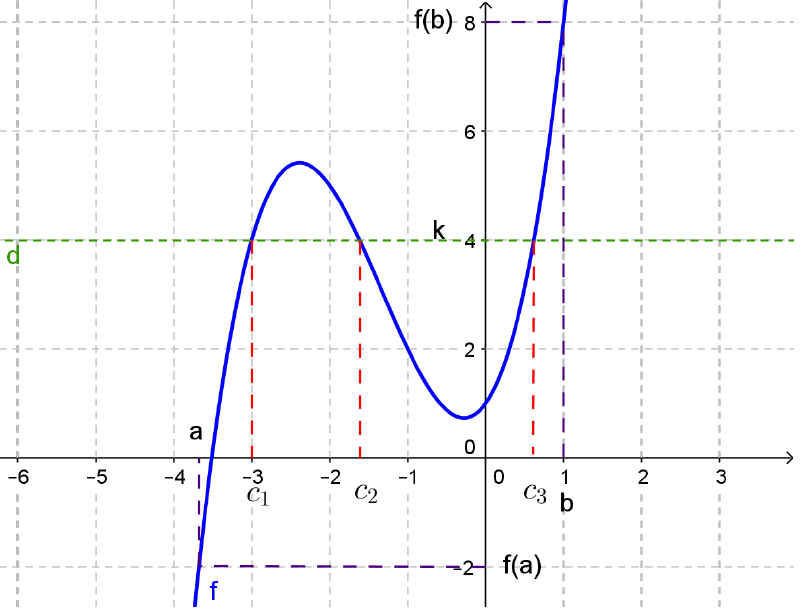
La fonction représentée en bleu est continue sur $I=[a,b]$.
Pour $k$ compris entre $f(a)$ et $f(b)$, on remarque graphiquement qu’il existe un $c_1$ dans $[a,b]$ tel que $f(c_1)=k$.
On voit, aussi qu’il existe deux autres $c_2$ et $c_3$ dans $[a,b]$ tels que $f(c_2)=k$ et $f(c_3)=k$. (D’où, dans le théorème, l’importance de l’expression “au moins”)
Cas des fonctions strictement monotones
Soit $f$ une fonction continue et strictement monotone sur un intervalle $[a,b]$ avec $a\leqslant b$.
Pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe un unique réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
Illustration graphique
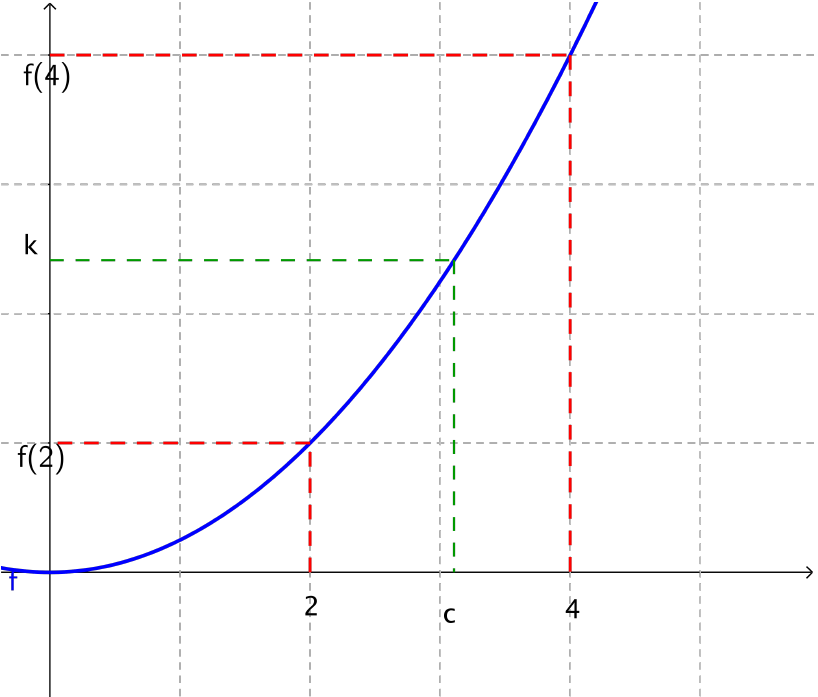
La fonction représentée en bleu est continue et strictement croissante sur $I=[2,4]$.
Pour $k$ compris entre $f(2)$ et $f(4)$, on remarque graphiquement qu’il existe un unique $c$ dans $[2,4]$ tel que $f(c)=k$.
Théorème des valeurs intermédiaires - Exercice
Soit \(f(x) = x – e^x + 2 \text{ avec } D_f = \mathbb{R}\).
Montrons qu’il existe une unique solution de \(f(x) = 0\) lorsque \(x \in [1 ; 2]\).
Ce qu’il faut savoir faire :
- Étape 1 : On précise que \(f\) est continue sur l’intervalle comme somme de fonctions continues.
- Étape 2 : On calcule la dérivée \(f’\) pour étudier les variations de \(f\).
- Étape 3 : On note que la fonction est strictement décroissante sur \([1 ; 2]\).
- Étape 4 : On calcule \(f(1)\) et \(f(2)\).
- Étape 5 : On applique le théorème des valeurs intermédiaires : il existe un unique réel \(\alpha\) tel que \(f(\alpha) = 0\).