Cinétique
Cinétique
Il existe deux types de réactions chimiques :
– les réactions chimiques instantanées pour lesquelles il n’est pas possible de mesurer et de constater l’évolution du système entre l’état initial et l’état final,
– les réactions chimiques lentes pour lesquelles il est possible de mesurer et de constater l’évolution du système entre l’état initial et l’état final.
La cinétique consiste en l’étude de l’évolution de la réaction chimique lente en fonction du temps, grâce à la mesure d’un paramètre variant lors de la réaction, comme le pH si la réaction met en jeu des acides et des bases, la conductance si la réaction met en jeu des espèces chargées ou encore l’absorbance si la réaction met en jeu des espèces colorées.
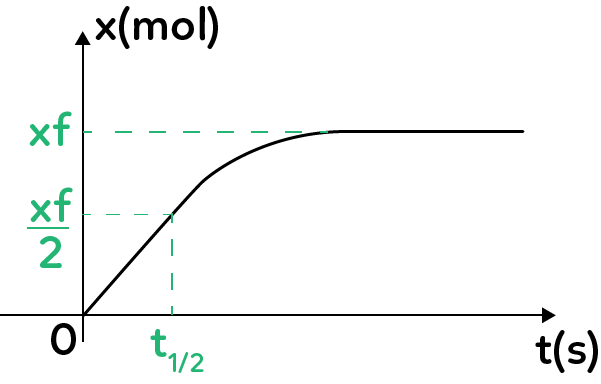
À l’issue de la mesure, il est possible de tracer l’évolution de l’avancement de la réaction $x$ (en mol) en fonction du temps. L’avancement a pour valeur 0 à l’état initial et $x_f$ à l’état final. $x_f$ est ainsi déterminé à partir de l’asymptote horizontale de la courbe.
Ces réactions sont caractérisées par le temps de demi-réaction $t_{1/2}$ qui est la durée au bout de laquelle l’avancement atteint la valeur $\dfrac{x_f}{2}$, que l’on détermine graphiquement à partir du calcul de la valeur $\dfrac{x_f}{2}$ dont on cherche ensuite l’abscisse associée.
Ce temps de demi-réaction est important pour caractériser les transformations chimiques lentes : une réaction est considérée comme finie pour un temps égal à environ 6 ou 7 fois $t_{1/2}$.
Des facteurs cinétiques permettent d’accélérer les réactions chimiques lentes :
– Une augmentation de la température augmente l’agitation des particules dans le système chimique augmentant ainsi la probabilité de rencontre entre réactifs : la réaction est donc accélérée.
– Une augmentation de la concentration des réactifs favorise la rencontre entre réactifs ce qui accélère également la réaction.
– Une augmentation de la surface de contact des réactifs est aussi un facteur cinétique : la transformation chimique entre le fer et l’acide chlorhydrique par exemple est beaucoup plus rapide lorsque le fer est en poudre que lorsqu’il est sous forme de lame.
Pour accélérer la réaction, des catalyseurs peuvent être utilisés. Un catalyseur est une espèce chimique qui accélère la réaction sans intervenir dans son bilan final : il est consommé puis régénéré lors de la transformation.
Il existe trois types de catalyse :
– l’homogène (le catalyseur est dans la même phase que les réactifs),
– l’hétérogène (le catalyseur n’est pas dans la même phase que les réactifs),
– l’enzymatique (on utilise des enzymes, des macromolécules d’origine biologique).
Vitesse de réaction
Vitesse de réaction
Lorsqu’on a une réaction lente, on va définir ce que sont la vitesse volumique d’apparition des produits et la vitesse volumique de disparition des réactifs.
On va considérer la réaction chimique d’équation $A + B \rightarrow C + D.$ C’est une équation de réaction très simple. Il n’y a pas de coefficients stœchiométriques dans cette équation.
Vitesse volumique d’apparition d’un produit
La vitesse volumique d’apparition d’un produit est la variation de la concentration en produit en fonction du temps :
$v = \dfrac{d[produit]}{dt}$.
On peut donc étudier la vitesse volumique d’apparition de $C$ et de $D.$ La vitesse volumique d’apparition d’un produit s’exprime en $mol.L^{-1}.s^{-1}$, la concentration en $mol.L^{-1}$ et le temps en $s.$
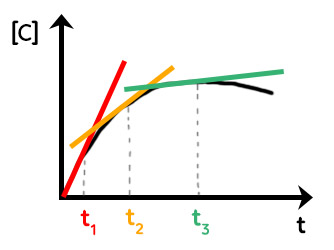
Concrètement, on a ce type de courbe :
Il exprime la concentration de $C$ en fonction du temps. Pour trouver la vitesse volumique d’apparition de $C$ en fonction du temps, on va tracer la tangente à la courbe à trois instants : $t_1, t_2, t_3.$
La vitesse volumique d’apparition de $C$ est le coefficient directeur de la tangente à la courbe. Plus la droite est verticale et plus le coefficient directeur est grand. Plus la droite est horizontale et plus le coefficient directeur est petit. Plus le temps passe et plus la vitesse volumique d’apparition du produit diminue. Cela est logique puisqu’avec le temps, la quantité de produits formés diminue.
Vitesse volumique de disparition d’un réactif
De la même manière, on définit la vitesse volumique de disparition d’un réactif. Elle est égale à : $v = -\dfrac{d[réactif]}{dt}$.
Au niveau des unités c’est exactement la même chose et il faut bien veiller à mettre ce signe ” – ” devant le quotient. La vitesse n’est pas négative, elle doit être positive dans ces cas-là. Puisque la concentration en réactif diminue au fil de la réaction, pour éviter d’avoir une vitesse négative, on ajoute un signe ” – ” devant.
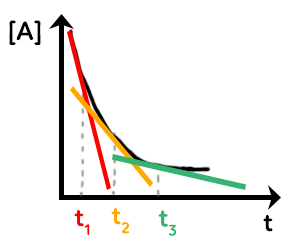
De la même manière, on aura ce type de courbe :
On étudie par exemple l’espèce $A$ avec sa concentration en fonction du temps. La vitesse volumique de disparition de $A $ sera le coefficient directeur de la tangente à la courbe à différents instants, ici $t_1, t_2$ et $t_3.$ Plus le temps passe et plus la tangente à la courbe devient horizontale. Donc, plus la réaction se passe et plus le coefficient directeur de la tangente à la courbe diminue et plus la vitesse volumique de disparition de $A$ diminue.
Il existe un cas particulier qui serait le cas de la vitesse d’ordre 1 par rapport à $A.$ Cela veut dire que la vitesse est proportionnelle à la concentration en $A. $ Il n’y a que l’expérience qui pourra déterminer ça. Par exemple, quand on trace la vitesse en fonction de la concentration en $A,$ on aura alors une droite qui passe par l’origine. C’est donc l’expérience et les conditions qui vont déterminer cette loi de vitesse d’ordre 1 par rapport à $A.$