Somme des angles d’un triangle
Somme des angles d’un triangle
Quelle est la propriété concernant la somme des angles d’un triangle ?
La somme des mesures des angles d’un triangle vaut 180°.
Exemple :
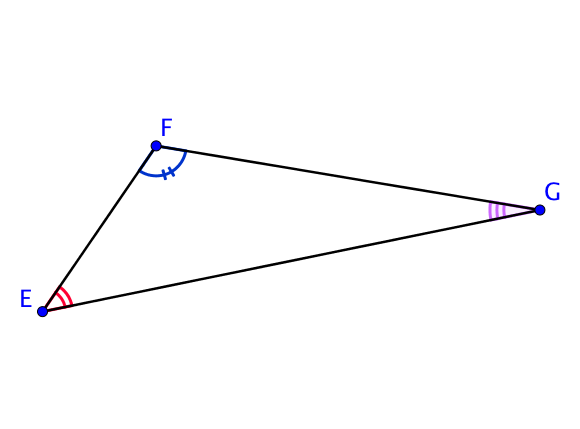
On se place dans le triangle $EFG$.
D’après la propriété précédente, on a l’égalité suivante :
$\widehat{EFG} + \widehat{FGE} + \widehat{GEF} = 180$ °.
Ainsi, en connaissant la mesure de deux angles, il est possible d’en déduire la valeur du dernier.
Exemple :
Supposons que $\widehat{EFG} = 100$° et $\widehat{GEF} = 50$°
Alors
$\widehat{EFG} + \widehat{FGE} + \widehat{GEF} = 100 + 50 + \widehat{FGE}$
$\widehat{EFG} + \widehat{FGE} + \widehat{GEF} = 150 + \widehat{FGE}$
On sait aussi que :
$\widehat{EFG} + \widehat{FGE} + \widehat{GEF} = 180$.
Ainsi,
$\widehat{FGE} = 180 – 150 = 30$°.
Cas particuliers :
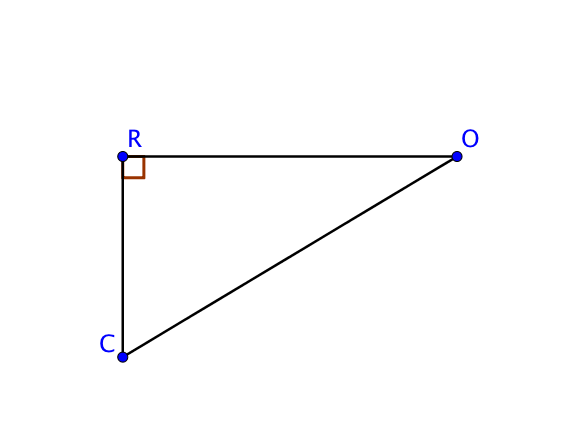
1) Le triangle rectangle
On sait que l’angle droit mesure 90°, donc $\widehat{ORC} = 90$°.
Ainsi,
$\widehat{ROC} + \widehat{OCR} = 180 – 90 = 90$°.
Qu’est-ce qu’un angle complémentaire ?
Deux angles dont la somme des mesures vaut $90$° s’appellent des angles complémentaires.
Les deux angles aigus $\widehat{ROC}$ et $\widehat{OCR}$ sont donc des angles complémentaires.
2) Le triangle isocèle
Quelles sont les propriétés du triangle isocèle ?
Par définition, un triangle isocèle est un triangle ayant deux côtés de même longueur.
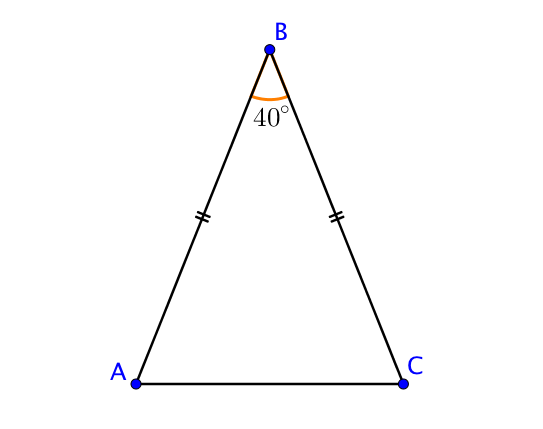
$ABC$ est un triangle isocèle en $B$, ce qui signifie que $BA = BC$ mais aussi que les deux angles à la base sont de même mesure.
Si on sait que $\widehat{ABC} = 40$°, on peut en déduire la valeur des autres angles.
En effet,
$\widehat{BCA} + \widehat{CAB} = 180 – 40$
$\widehat{BCA} + \widehat{CAB}= 140$°.
Or $\widehat{BCA} = \widehat{CAB}$, donc il mesure chacun la moitié de $140$.
Ainsi,
$\widehat{BCA} = \widehat{CAB} = 70$°
3) Le triangle équilatéral
Quelles sont les caractéristiques d’un triangle équilatéral ?
Un triangle équilatéral est un triangle ayant ses trois côtés de même longueur.
En outre, les angles d’un triangle équilatéral ont même mesure.
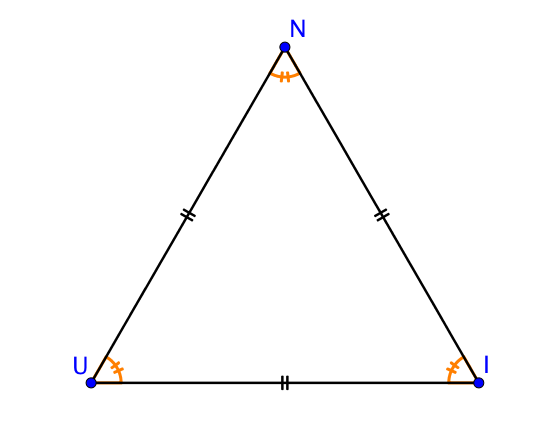
$UNI$ est un triangle équilatéral.
Chaque angle est égal et la somme vaut $180$°, ce qui signifie que chaque angle mesure le tiers de $180$°, c’est-à-dire $60$°.