Fonction racine carrée
Fonction racine carrée
Définition
La fonction racine carrée est une fonction définie sur $\mathbb{R}^+$ à valeurs dans $\mathbb{R}^+$ et on la note $\left \{ \begin{array}{ccccc} f & : & \mathbb{R}^+ & \to & \mathbb{R}^+ \\ & & x & \mapsto & \sqrt{x} \end{array} \right.$
La racine carrée d’un nombre négatif n’existe donc pas et le résultat est obligatoirement positif ou nul.
Variations
La fonction est strictement croissante et son tableau de variations est le suivant :
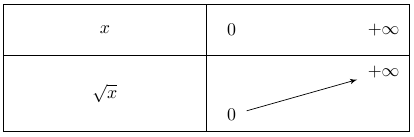
La démonstration de la croissance de la fonction racine carrée est exigible.
Soient $a$ et $b$ deux réels positifs tel que $a < b$,
On souhaite montrer que $\sqrt{a} < \sqrt{b}$.
Pour cela, on étudie le signe de la différence $\sqrt{b} – \sqrt{a}$.
On utilise donc l’expression conjuguée :
$ \begin{align} \sqrt{b} – \sqrt{a} &=& \dfrac{(\sqrt{b} – \sqrt{a})(\sqrt{b}+\sqrt{a})}{\sqrt{a}+\sqrt{b}} \\ &=& \dfrac{b – a}{\sqrt{a}+\sqrt{b}} \end{align}$
Or $b > a$ donc $ b – a > 0$. De plus, $\sqrt{a}+\sqrt{b}$ est toujours positif.
Ainsi, $\dfrac{b – a}{\sqrt{a}+\sqrt{b}} > 0$ ce qui revient à dire que $\sqrt{b} – \sqrt{a} > 0$ ou encore $\sqrt{b} > \sqrt{a}$.
Représentation graphique
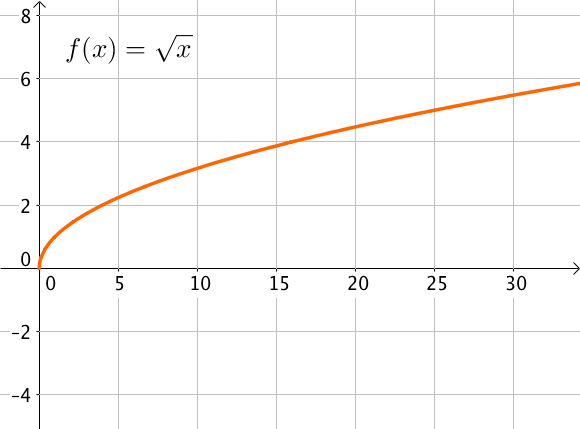
La position de la courbe représentation de la fonction racine carrée par rapport aux fonctions $y = x$ et $y = x^2$ est aussi à connaitre.
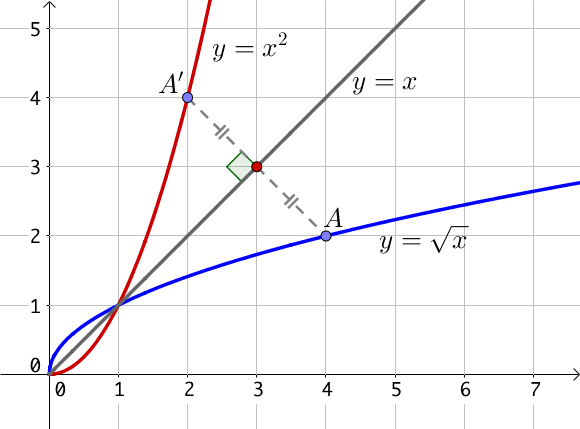
On remarque dans un premier temps que les fonctions $y = x^2$ et $y = \sqrt{x}$ sont symétriques par rapport à la droite d’équation $y = x$.
Pour $0 \leq x \leq 1$, la fonction $y = \sqrt{x}$ est au dessus de la fonction $y = x$ elle même au dessus de la fonction $y = x^2$.
Pour $x \geq 1$, l’ordre est inversé.
Les démonstrations de ces positions sont exigibles.
Pour étudier la position, on étudie le signe de $f(x) – g(x)$ où $f$ et $g$ sont deux fonctions parmi les trois en utilisant la quantité conjuguée lorsque l’une des fonctions sera la fonction racine carrée.
Etudions par exemple la position relative de $y = x$ par rapport à $y = \sqrt{x}$. On étudie alors le signe de $x – \sqrt{x}$:
Soit $x \in \mathbb{R}^+, \ x – \sqrt{x} \geq 0 \iff \dfrac{x^2 – x}{ x + \sqrt{x}} \iff x^2 – x \geq 0 \iff x(x – 1) \geq 0 \iff x – 1 \geq 0$ (car $x$ est toujours positif).
Ainsi, pour $x \geq 1$, la fonction $y = x$ est au dessus de la fonction racine carrée.
Pour $x \leq 1$, la fonction racine carrée est au dessus de la fonction $y = x$.
Fonction cube
Fonction cube
Définition
La fonction cube est une fonction définie sur $\mathbb{R}$ à valeurs dans $\mathbb{R}$ et se note $\left \{ \begin{array}{ccccc} f & : & \mathbb{R} & \to & \mathbb{R} \\ & & x & \mapsto & x^3 \end{array} \right.$.
Variations
Cette fonction est strictement croissante pour tout réel $x$.
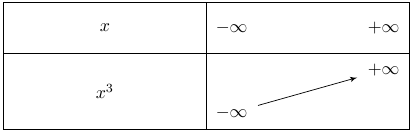
La représentation graphique de la fonction cube est la suivante :
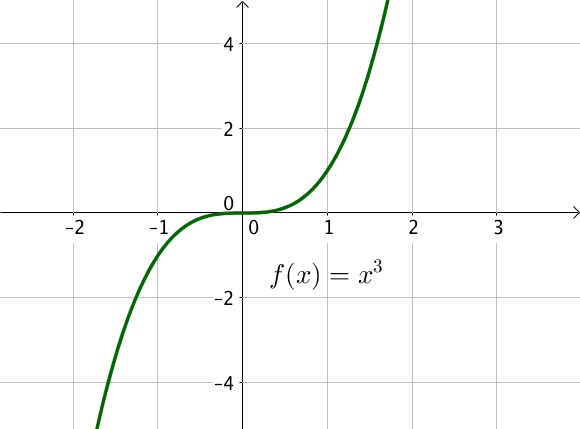
A retenir :
Pour tout $x \geq 0, \ x^3 \geq 0$
Pour tout $x \leq 0, \ x^3 \leq 0$.
Les fonctions $u$ et $u^3$ ont les mêmes variations.
Par exemple, pour étudier les variations de $(x+3)^3$, on peut étudier les variations de $x + 3$ puis en déduire celle de $(x+3)^3$.
Or on sait que $x + 3$ est une fonction croissante sur $\mathbb{R}$, ainsi, $(x+3)^3$ est aussi une fonction croissante.
Pour tous réels $a$ et $b$,
$a^3 – b^3 = (a – b)(a^2 + ab + b^2)$.
Fonction valeur absolue
Fonction Valeur absolue
Définition
La fonction valeur absolue est une fonction définie sur $\mathbb{R}$ à valeur dans $\mathbb{R}^+$ et on la note $\left \{ \begin{array}{ccccc} f & : & \mathbb{R} & \to & \mathbb{R}^+ \\ & & x & \mapsto & |x| \end{array} \right.$.
La valeur absolue d’un nombre positif est le nombre lui-même.
La valeur absolue d’un nombre négatif est son opposé.
En d’autres termes,
Si $x \geq 0, \ |x| = x$
Si $x \leq 0, \ |x| = -x$
La fonction est strictement décroissante pour $x$ négatif et strictement croissante pour $x$ positif.
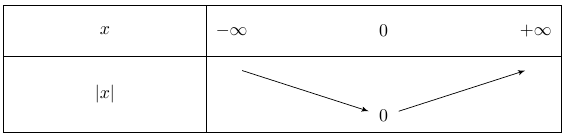
Sa représentation graphique est la suivante :
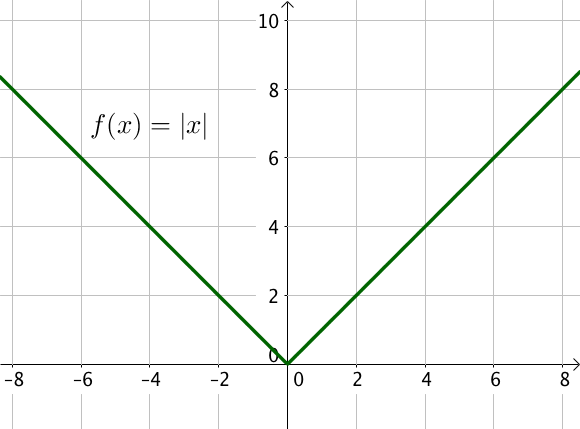
Propriétés
Pour tout $x \in \mathbb{R}, \sqrt{x^2} = |x|$.
Par exemple, $\sqrt{(-4)^2} = 4 = |-4|$.
Exemples :
$|-5| = 5$
$|7| = 7$
$|\sqrt{2} – 5| = – \sqrt{2} + 5$
$|\pi + 2| = \pi + 2$
$|\pi – 4| = 4 – \pi$
Pour étudier la fonction $f(x) = |x + 3|$, on étudie le signe de $x + 3$ en s’aidant d’un tableau de signe.
Si $x + 3 \geq 0$ alors $f(x) = x + 3$. Si $x + 3 \leq 0$ alors $f(x) = -(x + 3)$.


