Combustions
Combustions
I. Le triangle du feu

Pour avoir une combustion (quelque chose qui brûle), il faut absolument avoir trois choses présentes. Un combustible, ce qui va brûler (bois, papier, gaz, alcanes, alcools, etc), un comburant (dioxygène) et une énergie d’activation (étincelle, etc).
Dans le cas du briquet, le combustible est le gaz présent à l’intérieur du briquet, le comburant est le dioxygène de l’air et l’énergie d’activation est soit électrique soit mécanique par le frottement engendré par la rotation de la molette.
II. Oxydation du combustible
Une combustion est une réaction chimique, c’est une oxydation du combustible. Elle fait partie des réactions d’oxydo-réduction. Cette combustion peut être complète ou incomplète.
– Si la combustion est complète, on aura les produits H2O et CO2. On aura uniquement CO2 dans le cas de la combustion du carbone et H2O dans le cas de la combustion du dihydrogène. On a l’équation d’oxydation complète de l’éthanol :
$C_2H_6O(l) + 3O_2(g) \rightarrow 2CO_2(g) + 3H_2O(l)$
Attention à ce qu’elle soit équilibrée. On commencera par équilibrer les C, les H puis les O.
– Si la combustion est incomplète, on obtiendra du carbone (C) et du monoxyde de carbone (CO). Le CO est très dangereux car il est inodore, incolore et sans saveur et va se fixer sur les globules rouges et provoquer des intoxications.
III. Aspect énergétique
On doit connaître le pouvoir calorifique (PC) qui correspond à l’énergie dégagée par la combustion d’un kilogramme de combustible. Il y a un PC pour chaque combustible, qui est donné dans les exercices ou que l’on devra retrouver.
Par exemple : PC(C2H6O) = 29 MJ.kg-1 et PC(bois) = 15 MJ.kg-1.
On peut être amené à calculer l’énergie libérée dans une combustion. Pour cela on a la formule : $Q = m \times PC$, avec $Q$ en joules, $m$ la masse en kg et $PC$ le pouvoir calorifique en J.kg-1. Ce sont souvent des nombres très grands donc attention aux conversions !
Enfin, on doit avoir quelques connaissances sur les combustions. Le problème lié aux combustions est qu’elles sont très dangereuses, le carbone et la vapeur d’eau sont des gaz à effet de serre, les combustibles sont souvent des sources d’énergies non renouvelables (exploitées plus vite que renouvelées). On est actuellement en train de trouver des alternatives avec notamment les agrocarburants.
Énergie de réaction
Énergie de réaction
I. Énergie de liaison
Comment calcule-t-on une énergie de réaction ? Il est d’abord important de définir l’énergie de liaison.
On la note $E_{A-B}$ (en $J.mol^{-1}$) et c’est l’énergie qu’il faut fournir pour rompre la liaison entre un atome $A$ et un atome $B$ en phase gazeuse.
C’est pour cela qu’on associe cette énergie à cette réaction : $A-B(g) \to A(g) + B(g)$.
Exemple :
L’énergie de la liaison $O-H$ vaut : $E_{O-H}=463 \ kJ.mol^{-1}$.
II. Énergie molaire de réaction
Ensuite on peut calculer l’énergie molaire de réaction. On la note $\Delta E$ en $J.mol^{-1}.$
Cette énergie vaut : $\Delta E= \sum E_{liaisons \ rompues} – \sum E_{liaisons \ formées}$
Exemple :
On prend pour exemple la réaction de combustion du méthane : $CH_4 + 2O_2 \to CO_2 + 2 H_2O$.
Les formules développées des molécules sont :
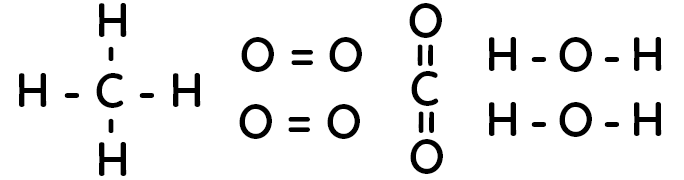
Lors de cette réaction chimique, on a donc :
– liaisons rompues : 4 liaisons $C-H$ et 2 doubles liaisons $O=O$
– liaisons formées : 2 doubles liaisons $C=O$ et 4 liaisons $O-H$
Ainsi, l’énergie molaire de réaction est : $ \Delta E = 4 E_{C-H} + 2 E_{O=O} – 2 E_{C=O} – 4 E_{O-H} = -804 \ kJ.mol^{-1}$
Ceci signifie que la combustion du méthane libère $804 \ kJ.mol^{-1}$ car le signe de $\Delta E$ est négatif, la réaction est exothermique comme toutes les combustions.


