Désintégration radioactive et notions de demi-vie
Désintégration radioactive et notions de demi-vie
I. Les désintégration radioactives
A. Principe
Un atome est composé d’un noyau autour duquel gravitent des électrons. Certains noyaux d’atomes sont instables, ceci est dû au fait qu’ils possèdent soit trop de protons (surplus de protons) ou trop de neutrons (surplus de neutrons) ou bien les deux.
En effet, un noyau est composé de neutron(s) et de proton(s), que l’on appelle nucléons. Ces noyaux instables sont trop lourds, ils vont donc se désintégrer et donner des noyaux plus légers. Par exemple, le carbone 14 que l’on étudie en SVT car il permet de faire de la datation.
B. Graphique
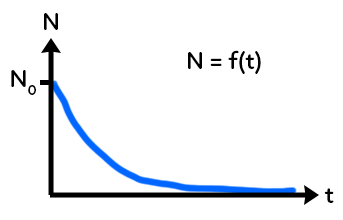
Graphiquement, le nombre de noyaux $N$ diminue au cours du temps car les noyaux initiaux $N_0$ se désintègrent jusqu’à disparaître totalement au bout d’un certain temps $t.$
Ce phénomène s’appelle la décroissance radioactive.
II. Notion de demi-vie
Définition
La notion de demi-vie est le temps au bout duquel le nombre de noyaux présents initialement a été divisé par deux. Elle se note t½ et elle est caractéristique d’un noyau donné, à chaque noyau correspond une unique demi-vie.
On considère un nombre de noyaux initiaux $N_0,$ alors au bout d’une demi-vie c’est-à-dire :
$1 times t^{frac{1}{2}},$ il reste $dfrac{N_0}{2}$ noyaux.
Ensuite au bout de deux demi-vies, c’est-à-dire $2 times t^{frac{1}{2}},$ il reste la moitié de ce qu’il y avait au bout d’une demi-vie, il reste donc :
$dfrac{N_0}{2} times dfrac{1}{2} = dfrac{N_0}{4} = dfrac{N_0}{2^2}$.
De même pour $3 times t^{frac{1}{2}}$ : la quantité initiale est $dfrac{N_0}{4}$ et on la divise par $2,$ il reste alors :
$dfrac{N_0}{4} times dfrac{1}{2} = dfrac{N_0}{8} = dfrac{N_0}{2^3}$.
On peut généraliser pour $n times t^{frac{1}{2}},$ on divise la quantité initiale de noyaux $N_0$ par $2 n$ fois, il reste alors à la fin $dfrac{N_0}{2^n}$.
III. Exploitation des représentations graphiques
Les représentations graphiques permettent de déterminer certains valeurs particulières.
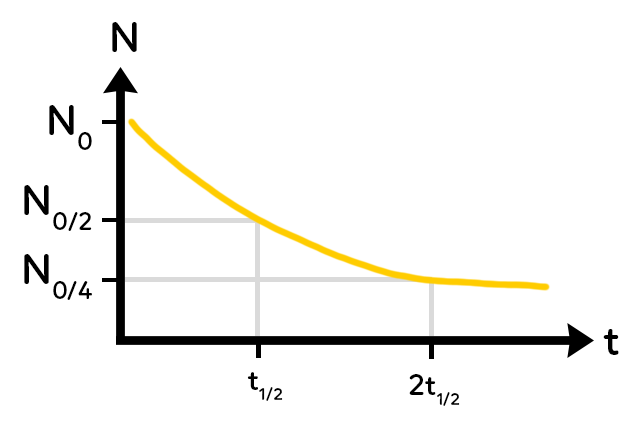
A. Déterminer t½
On peut tout d’abord déterminer le temps de demi-vie : il correspond au moment où il ne reste plus que la moitié des noyaux initiaux.
On peut aussi déterminer le temps $2 times t^{frac{1}{2}}$ puisque ce temps correspond au moment où il ne reste plus que $dfrac{N_0}{4}$ noyaux.
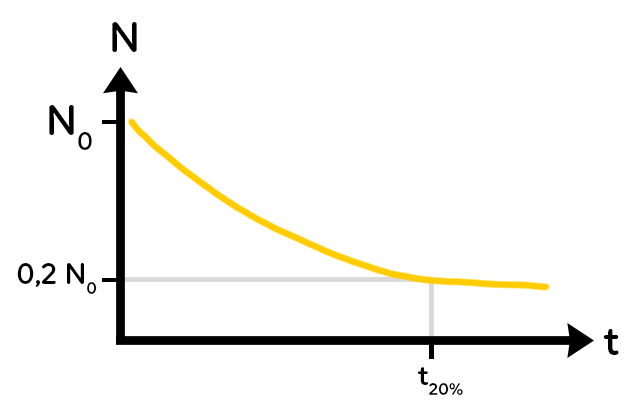
B. Déterminer un temps pour un pourcentage de noyaux restants
On peut déterminer un temps au bout duquel il reste un certain pourcentage de noyaux. Par exemple, la question pourrait être : trouver $t$ pour lequel 80 % des noyaux ont été désintégrés.
Alors si 80% des noyaux ont été désintégrés, c’est qu’il reste 20 % des noyaux initiaux, c’est à dire $0.2 times N_0.$ Il suffit alors de placer $0.2 times N_0$ sur l’axe des ordonnées, et on peut trouver, en faisant une construction graphique le temps qui correspond à 20 % de noyaux restants, c’est-à-dire 80 % de noyaux désintégrés.
Abondance des éléments sur Terre et dans les êtres vivants
Abondance des éléments sur Terre et dans les êtres vivants
I. Abondance relative des éléments chimiques de la croûte terrestre et des êtres vivants
« Les éléments », on entend par là les éléments chimiques (les atomes :carbone, hydrogène, oxygène, etc). On pourrait partir de l’histogramme ci-dessous qui donne l’abondance relative des éléments chimiques exprimée en pourcentage du nombre total d’atomes.
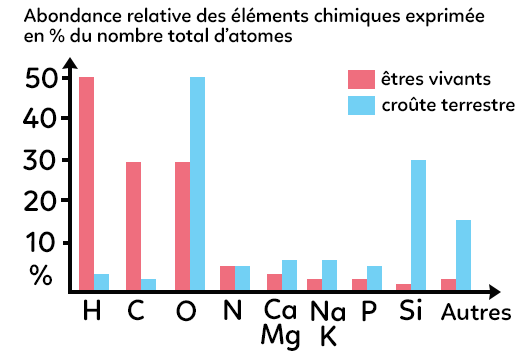
On compare ici en rouge l’abondance relative des éléments chimiques constitutifs des êtres vivants (les tissus mous exclusivement pour cet histogramme) et en bleu l’abondance relative des éléments chimiques constitutifs de la croûte terrestre.
Ce qui apparaît évident c’est l’importante richesse en éléments hydrogène chez les êtres vivants, en carbone, en oxygène essentiellement. Donc C, H, O semblent être les éléments chimiques, les atomes, constitutifs des êtres vivants.
Comparativement, en bleu, on constate que la croûte terrestre est plutôt riche en oxygène (O) et en silicium (Si).
II. Être vivant
Quelle est la notion de vie et d’être vivant ?
Définition : un être vivant est un ensemble de molécules (une molécule est un assemblage d’éléments chimiques, d’atomes) organiques (tout ce qui présente surtout du carbone) mais aussi de molécules minérales.
Ces molécules organiques et ces molécules minérales, sont constamment fabriquées, synthétisées et dégradées. De sorte que, finalement, les êtres vivants sont traversés de processus chimiques et physiques qui vont vers un ordre. L’Univers va constamment vers un désordre constant, et quand on range, quand on fabrique ou synthétise des molécules, cela demande de l’énergie. Donc finalement quand on est vivant, on est traversé de flux énergétiques que cet organisme vivant va être capable de convertir et d’utiliser à des fins de construction.
Etre vivant c’est constamment aller vers un certain ordre de la matière. Quand on meurt, c’est le désordre total et on restitue les éléments chimiques, les atomes qu’on a emprunté à notre environnement pour un futur individu vivant.
III. Classer les molécules
On peut classer les molécules entre les organiques et les minérales. Regardons de nouveau l’histogramme.
A. Molécules minérales
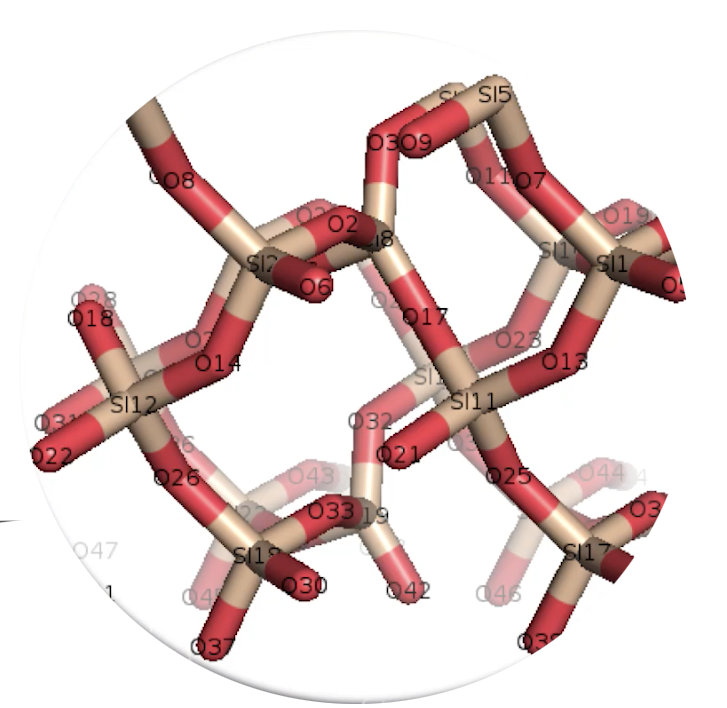
– Si on regarde la représentation en 3D d’une molécule de quartz SiO2 (ci-dessus), on voit qu’il est fait de silicium et d’oxygène donc on met cette molécule plutôt dans le domaine du minéral. Ce n’est pas vivant, il n’y a pas de carbone ni d’hydrogène.
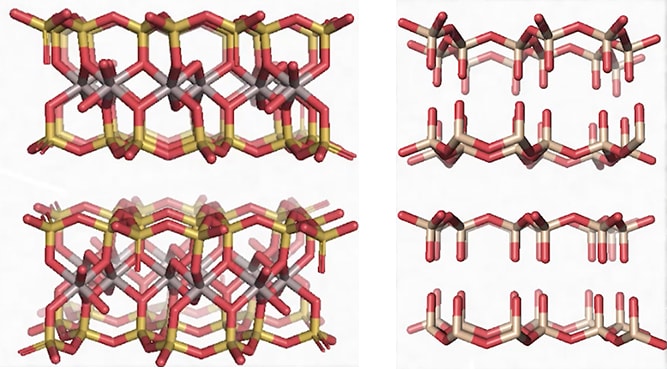
– Si on regarde la représentation en 3D d’une molécule de mica (deux formes différentes de mica) : muscovite (à gauche) ou biotite (à droite), on voit qu’il s’agit bien d’une molécule formée d’atomes liés entre-eux par des liaisons covalentes mais il n’y a pas d’atomes de carbone ou d’hydrogène : on est dans de la matière inerte, dans de la matière minérale.
B. Molécules organiques
Glucides
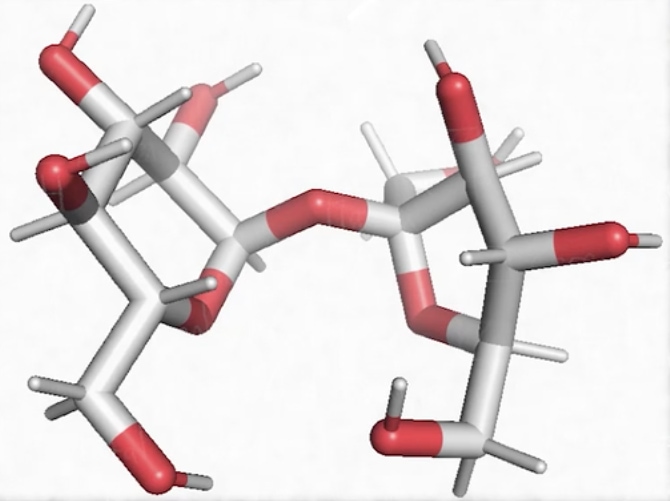
Voici une molécule de glucose, on reconnaît ici l’élément carbone qui apparaît en gris sur cette représentation (mais généralement on le représente en noir), lié de manière covalente à au moins un atome d’hydrogène : il s’agit d’une molécule organique, du vivant. Donc le glucose appartient à une grande famille qui s’appelle les glucides et qui sont des composés ternaires faits de 3 éléments chimiques : C, H et O.
Un autre exemple de glucide avec le saccharose: on remarque du gris pour le carbone, du blanc pour l’hydrogène et enfin du rouge pour l’oxygène.
Lipides
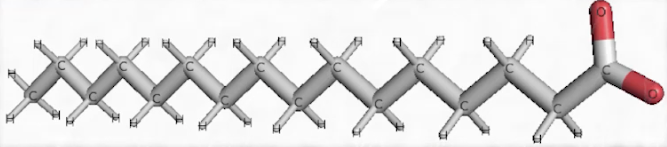
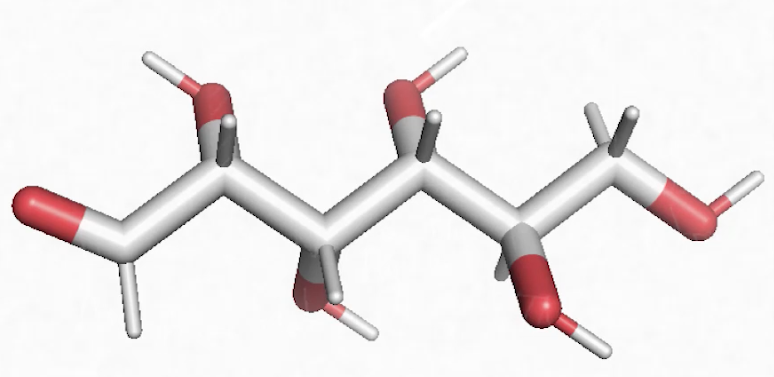
Voici une molécule qui s’appelle l’acide palmitique, qu’on retrouve dans l’huile de palme. On constate que c’est une longue chaîne grise, on dit une longue chaîne carbonée, liée de manière covalente à des atomes d’hydrogène : C, H. On est bien en face d’une molécule organique. Il y a, à la fin de cette longue chaîne carbonée, de l’oxygène. Là encore, on a un composé ternaire fait de 3 éléments chimiques, C, H, O : c’est du vivant.
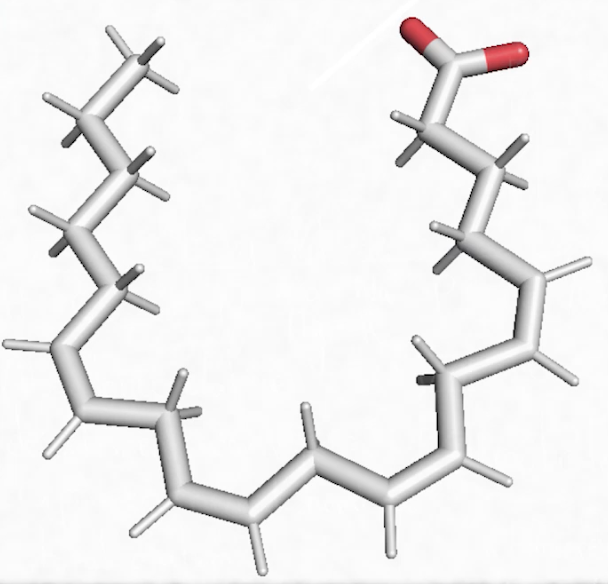
Un autre exemple de lipide avec l’acide arachidonique qu’on trouve dans l’huile d’arachide et là encore on constate une longue chaîne carbonée grise, donc du carbone, liée à des atomes d’hydrogène (C, H). On est bien en face d’un composé organique, avec de l’oxygène. C, H, O, c’est un lipide.
Protéines
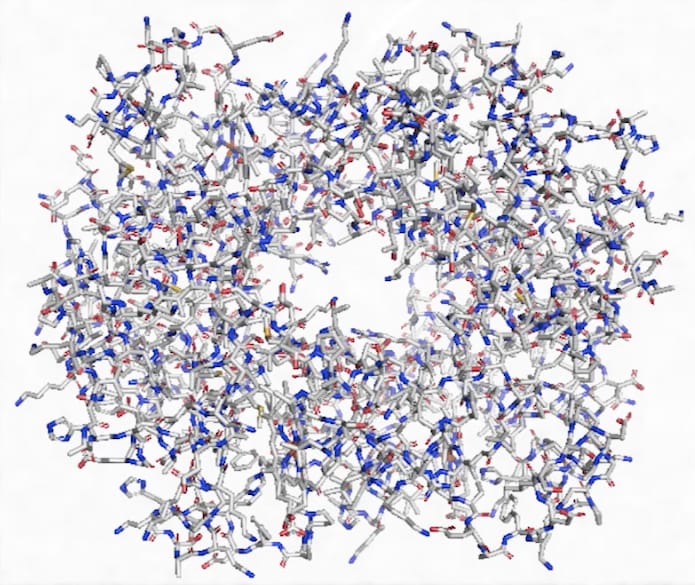
Dans la famille des protéines, voici une molécule l’insuline, une molécule très complexe comprenant beaucoup d’éléments chimiques qu’il est difficile de distinguer sur cette représentation : du carbone en gris, de l’hydrogène en blanc, de l’oxygène en rouge (C, H, O), mais aussi de l’azote en bleu, et du soufre en jaune (C, H, O, N, S). C, H sont présents donc on est en face d’une molécule organique.
Un autre exemple de protéine : l’hémoglobine, qui finit en « ine » comme « protéine », « insuline ». Là encore, c’est un composé fait de H, de O, de N, et de S.
Nucléotides
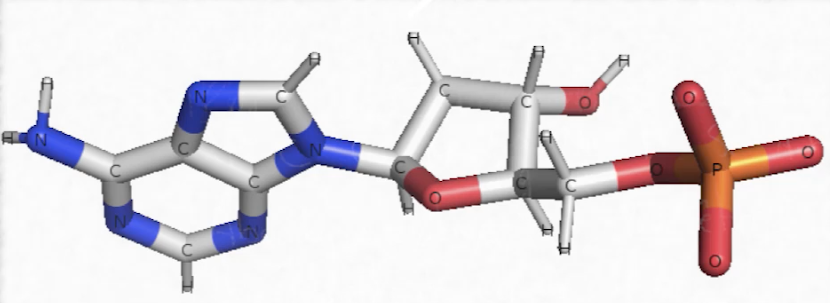
Voilà un exemple de nucléotide, c’est un élément constitutif de l’ADN qui se nomme l’adénine. Si on regarde sa composition, il faut identifier le carbone en gris, l’hydrogène en blanc (C, H : c’est bien de l’organique), de l’oxygène en rouge, mais aussi de l’azote en bleu (C, H, O, N) et enfin il y a du phosphore (donc C, H, O, N, P) donc c’est constitutif typique des nucléotides que l’on retrouve dans des acides nucléiques tels que l’ADN (acide désoxyribonucléique) ou encore l’ARN (acide ribonucléique).
Conclusion
Les molécules organiques constitutives du vivant présentent un carbone, un atome tétravalent (qui effectue 4 liaisons chimiques avec d’autres éléments chimiques) mais pour être organique le carbone est nécessairement dit réduit, c’est-à-dire lié de manière covalente à au moins un atome d’hydrogène.
Si on a C, H, O on est dans la famille des glucides ou des lipides. Ces molécules sont très énergétiques. Quand on rompt les liaisons entre le carbone et l’hydrogène, on libère beaucoup d’énergie.
Les protides C, H, O, N, S sont des molécules moins énergétiques mais qui ont un rôle fonctionnel et informationnel important.
Enfin les nucléotides C, H, O, N, P sont des molécules à rôle strictement informationnel.
Pour savoir si une molécule est une molécule organique ou minérale, il est possible de voir si elle est combustible. Parce que un carbone réduit lié à au moins une molécule d’hydrogène, donne une propriété chimique : dans l’atmosphère oxydante (l’atmosphère riche en O2), cette molécule est combustible. Elle brûle. En brûlant, elle libère du CO2, ; H2O et de l’énergie sous forme de lumière et/ou de chaleur.
Donc une molécule organique combustible est caractéristique du vivant comparativement au minéral surtout Si et O, avec du fer, du magnésium.
Désintégration radioactive et datation absolue
Désintégration radioactive et datation absolue
La désintégration radioactive et la datation absolue est abordée ici à travers le cas du carbone 14. L’élément carbone est très abondant dans la matière organique, on le trouver par exemple dans le charbon qui est un hydrocarbure issu de la matière organique. Ce charbon peut être utilisé dans les peintures rupestres par exemple à Lascaux ou dans la grotte de Chauvet.
I. Différents isotopes
Le carbone présente différents isotopes. Qu’est-ce qu’un isotope ?
Un élément chimique (comme le carbone) désigne l’ensemble des atomes dont le noyau compte un nombre donné de protons. On note ce nombre $Z$ et on l’appelle numéro atomique. Des atomes possédant le même numéro atomique (ils correspondent donc au même élément chimique) peuvent par contre différer de par le nombre de neutrons ($N$) contenus dans leur noyau. On dit que ces atomes sont des isotopes. Ils diffèrent entre eux de par leur nombre de masse (puisqu’il est la somme de $Z$ et $N$).
L’élément carbone est caractérisé par son numéro atomique $Z,$ qui vaut 6, et un nombre de masse $Z+N$ variable selon l’isotope de carbone auquel il correspond : carbone 12 ($Z+N=12$ et $N=12-7=5$) ; carbone 13 ($Z+N=13$ et $N=13-7=6$) ou carbone 14 ($Z+N=14$ et $Z=14-7=7$). Le carbone est, comme tout élément chimique, caractérisé par un nombre fixe de protons et un nombre variable de neutrons. L’élément carbone présente différents isotopes dont des isotopes radiogéniques (isotope issu de réactions de désintégrations nucléaires) comme le carbone 14.
II. Courbe de désintégration radioactive
Le carbone 14 a une particularité : il peut se désintégrer (désintégration au cours de laquelle le carbone transforme, pour simplifier, un neutron en proton : il change de numéro atomique et devient ici de l’azote ($Z=7$)) en un élément fils qui est l’azote 14.
L’élément chimique père est le carbone 14, l’élément chimique fils est l’azote 14. Cette désintégration est spontanée. Elle ne dépend que d’une seule variable qui est le temps.
On a défini en mathématiques la loi exponentielle de désintégration de décroissance radioactive.
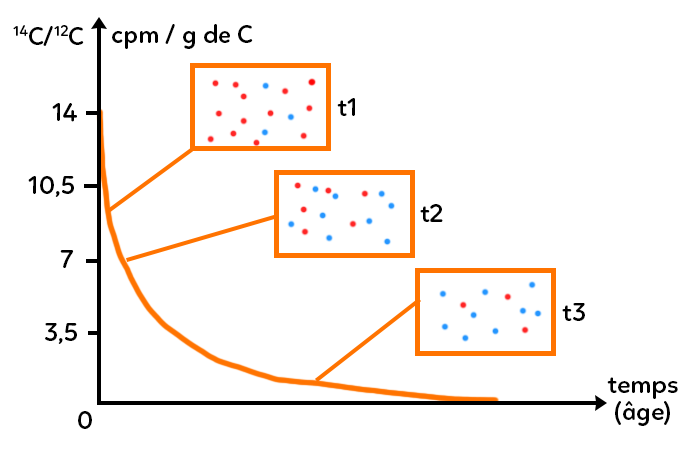
À $t=0,$ c’est le nombre d’éléments père à un instant $t$ : il décroît avec une seule variable, le temps. C’est inversement proportionnel au nombre d’éléments fils qui croît avec le temps. Ce qui est représenté en ordonnée est le rapport carbone 14 sur une constante, le carbone 12 (qui est l’isotope majoritaire dans l’atmosphère). Étudier un rapport sur une constante plutôt qu’une quantité directement permet de s’affranchir de l’impact de la taille de l’échantillon prélevé quand on fait de la datation absolue. On aurait la courbe rigoureusement inversement proportionnelle pour l’élément fils azote 14.
Si l’on représente par des points rouges l’élément carbone 14 et par des points bleus l’élément azote fils (l’élément azote 14), que se passe-t-il ?
– Au début (t1), il y a essentiellement des pères, qui se sont désintégrés, il n’y en a que deux car ici il y a seulement deux fils.
– Plus le temps passe (t2), moins il y a de pères et plus il y a de fils. Autrement dit, on a de moins en moins de points rouges et de plus en plus de points bleus.
Tout cela est vrai sous l’hypothèse que l’on étudie un système clos : dans les peintures rupestres on n’a pas rajouté au fur et à mesure du carbone, que le système une fois produit n’échange pas de matière avec son environnement.
– À la fin (t3), pratiquement la totalité de l’échantillon initial, qui ne contenait que du père (que du carbone 14), est devenu de l’azote 14 (élément fils).
La courbe de désintégration radioactive du carbone 14 a une allure exponentielle ici qui suit l’expression $N=N_0e^{-lambda t}.$ Le nombre d’éléments à un instant $t$ est égal au nombre initial fois exponentielle de $-lambda t.$ $lambda$ représente la constante de désintégration du carbone 14.
III. Datation absolue
Puisque la loi de désintégration ne dépend que d’une variable, le temps, la quantité d’éléments père qui deviendra fils est caractérisée par un temps de demi-vie.
Le temps de demi-vie correspond au temps pour lequel la moitié d’un échantillon s’est désintégré. Cette durée est constante et indépendante de la quantité initiale considérée. Elle dépend de la constante de désintégration de l’élément considéré. Dans le cas du carbone 14, la demi-vie vaut 5 730 ans plus ou moins 40 ans.
Cela signifie graphiquement que si on part avec un taux initial de 14 coups par minute (le coup par minute est une unité permettant de mesurer non pas l’activité radioactive d’une source mais son taux de comptage, c’est-à-dire le nombre de désintégrations par unité de temps détectées dans l’échantillon source et permet d’estimer la quantité d’éléments radioactifs contenus dans l’échantillon), alors à 7 coups par minute, pile la moitié (la moitié de l’échantillon, la moitié des éléments pères seront alors devenus des fils par désintégration) on se rend compte qu’en abscisse on a bien mis 5 730 ans à atteindre cette valeur deux fois plus petite que la valeur initiale.
Cette demi-vie est intéressante pour le couple carbone 14/azote 14 car elle permet de dater beaucoup d’éléments notamment type préhistoire, datés de jusqu’au plus 50 000 ans et minimum 500 ans.
IV. Cas concret
On récupère un échantillon de peinture de la grotte de Lascaux et on récupère du carbone 14. Via un spectromètre de masse, on mesure une désintégration d’à peu près 1,64 coups par minute par gramme de carbone. Comment utiliser cette donnée pour dater la grotte de Lascaux ?
Avec la loi de désintégration, à 1,64, on regarde en abscisse à quoi cela correspond et on lit 17 450 ans. Si on compare à la grotte de Chauvet, le spectromètre de masse m’affiche 0,323 coup par minute par gramme de carbone, ce qui permet de dater les peintures de cette grotte à 30 900 ans.
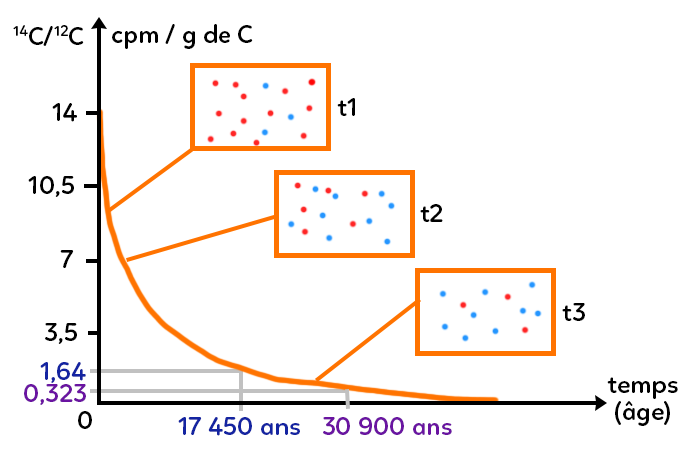
On remarque que c’est inférieur à 1,64. Cela signifie qu’il y a beaucoup d’éléments pères qui sont devenus des fils. Autrement dit, cet échantillon de Chauvet est beaucoup plus vieux que celui de Lascaux. Pour la grotte de Chauvet, on trouve un âge de 30 900 ans pour les peintures rupestres (temps correspondant en abscisse à 0,323 cpm/g de C). Autrement dit, à Chauvet on peut dater les peintures à 30 900 ans grâce au carbone 14 et celles de Lascaux à 17 450 ans.


