Parallélogrammes
Parallélogramme – définition
I) Définition
Un parallélogramme est un quadrilatère (figure à quatre côtés) dont les côtés opposés sont parallèles.
Pour nommer un parallélogramme, on nomme chacun de ses sommets puis on lit les sommets en partant d’un point et en tournant dans le même sens.
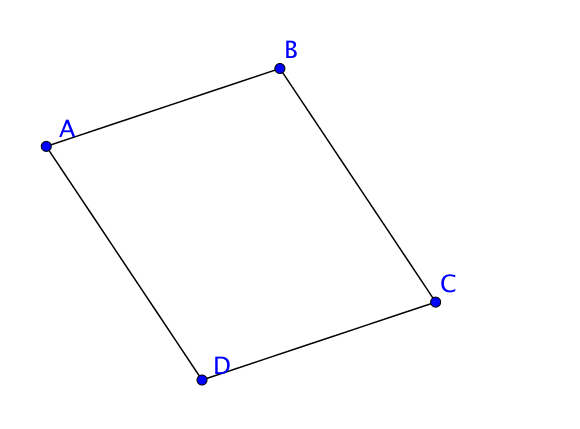
On peut appeler le parallélogramme suivant :
- $ABCD$
- $ADCB$
- $BADC$
II) Constructions
1) Construire un parallélogramme $IJKL$ tel que $IJ = 2$ cm et $JK = 3$ cm.
On commence tout d’abord par faire un schéma à main levée en respectant le nom du parallélogramme et en plaçant les valeurs numériques de l’énoncé.
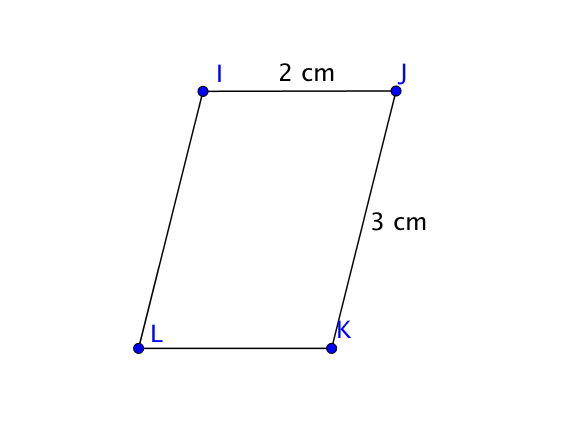
Pour faire la construction, on place les points $I$, $J$ et $K$ en respectant les longueurs données.
On trace ensuite la parallèle à $(IJ)$ passant par $K$ puis la parallèle à $(JK)$ passant par $I$.
Le point d’intersection des deux droites est le point $L$.
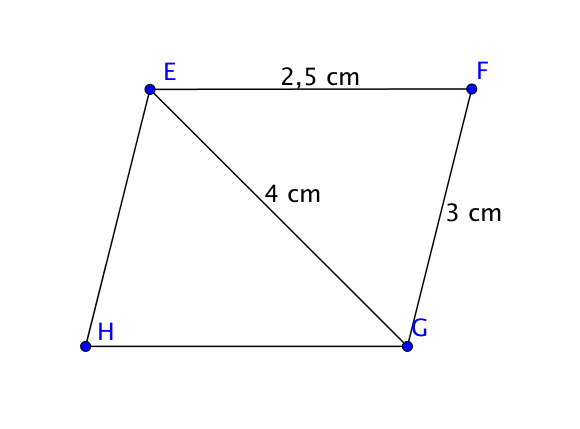
2) Construire le parallélogramme $EFGH$ tel que $EF = 2,5$ cm, $EG = 4$cm et $FG = 3$cm.
En faisant le schéma à main levée, on s’aperçoit que $[EG]$ est une diagonale.
Pour faire la construction, on commence par le triangle $EFG$ à l’aide du compas puis on termine en utilisant le parallélisme.
3) Construire le parallélogramme $RSTU$ tel que $RS = 4$cm et $ST = 3$cm et $\widehat{RST} = 65$°.
De même que précédemment, on débute l’exercice en traçant un schéma à main levée.
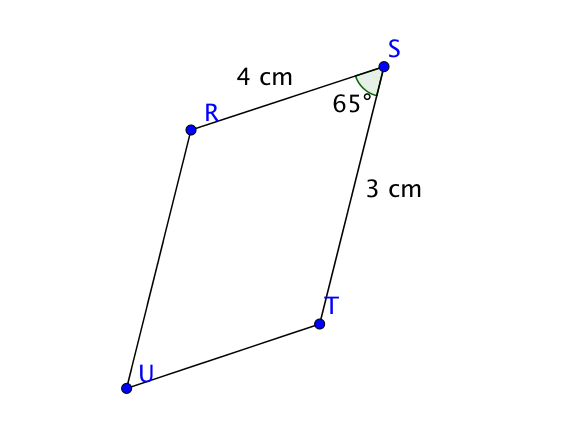
On commence ensuite par tracer le segment $[RS]$ puis à l’aide d’un rapporteur on construit l’angle $\widehat{RST}$ en traçant une droite d’origine $S$ puis on place le point $T$ distant de $3$cm de $S$.
Finalement, on utilise à nouveau le parallélisme pour terminer la construction.


