Fonction carré
La Fonction carré
Définition
La fonction carré est la fonction qui à tout réel $x$ associe $x^2$, c’est à dire $f(x) = x^2$ pour tout $x \in \mathbb{R}$.
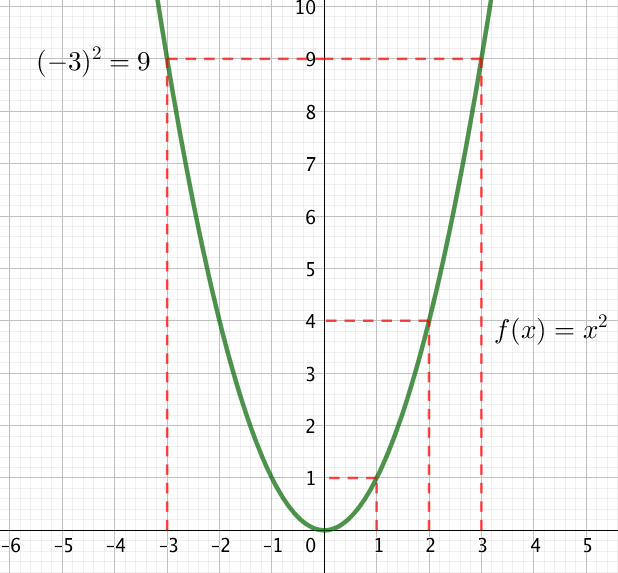
On peut construire sa représentation graphique point par point.
En effet, $0^2 = 0, \ 1^1 = 1, \ 2^2 = 4,…$.
Puis on relit ces différents points.
Sa représentation graphique est une parabole.
Variations
La fonction carré est décroissante pour $x$ négatif et croissante pour $x$ positif.
Son tableau de variation est le suivant :
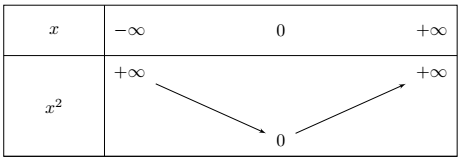
La fonction admet un minimum atteint en $x = 0$. Cette fonction admet un axe de symétrie (l’axe des ordonnées) : c’est une fonction paire.
Résolution graphique d’équations et d’inéquations
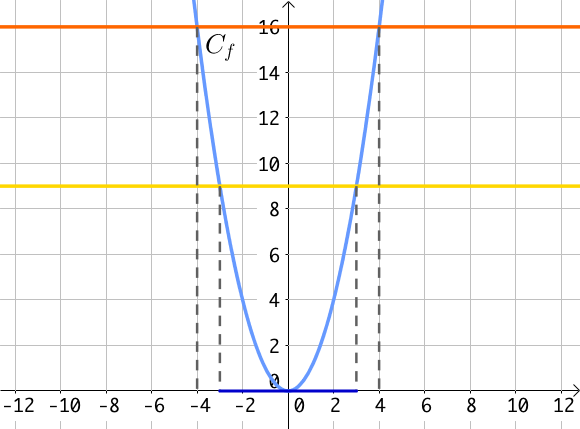
On veut résoudre graphiquement l’équation $f(x) = 16$, c’est à dire on souhaite déterminer les antécédents de 16 par la fonction $f$.
On trace une droite horizontale passant par le point de coordonnées $(0; 16)$ et les solutions de l’équation sont alors les abscisses des points d’intersection entre la droite horizontale et la courbe $C_f$ de la fonction carré.
On trouve alors comme solution $S = \{-4; 4\}$.
On souhaite désormais résoudre l’inéquation $f(x) \leq 9$.
Pour se faire, il faut repérer la portion de courbe pour laquelle les images sont inférieures à $9$ : cela correspond à la zone bleu foncé sur l’axe des abscisses
$S = [-3: 3]$.
Fonctions linéaires et affines
Fonctions linéaires et affines
Définition
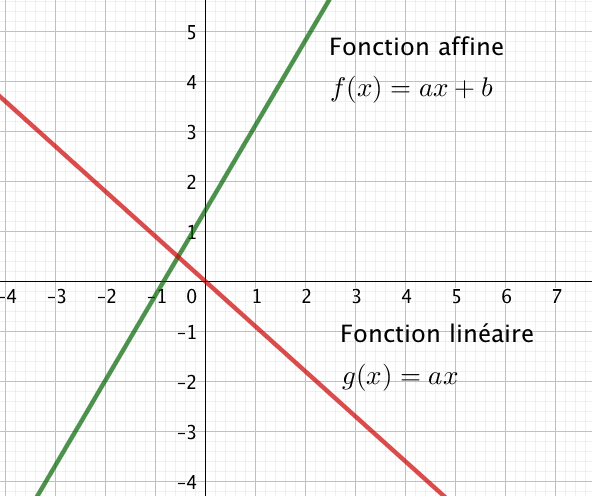
Une fonction affine est une fonction de la forme : $f(x) = ax + b$
Le nombre $a$ est le coefficient directeur de la droite, c’est à dire celui qui donne la pente de la droite, $x$ est la variable.
Le nombre $b$ l’ordonnée à l’origine, c’est à dire la valeur de la fonction lorsque $x = 0$.
Une fonction linéaire est une fonction affine particulière où $b = 0$ :
$g(x) = ax$, il s’agit d’une droite passant par l’origine.
Variations de fonctions affines
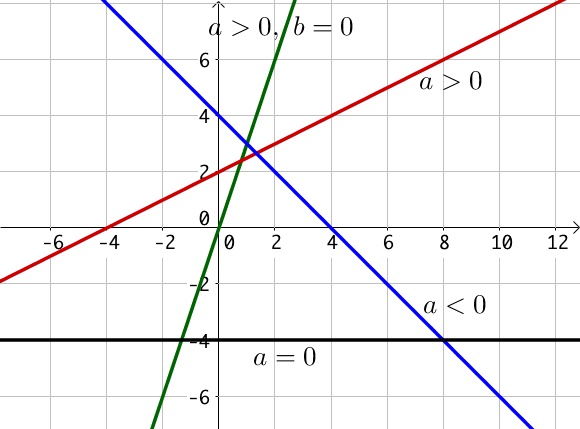
Si le coefficient directeur est strictement positif, alors la fonction $f$ est croissante sur $\mathbb{R}$.
Si le coefficient directeur est strictement négatif, alors la fonction $f$ est décroissante sur $\mathbb{R}$.
Si le coefficient directeur est nul, $f$ est constante sur $\mathbb{R}$ dont la représentation graphique est une droite parallèle à l’axe des abscisses.
Signe de $f(x)$
On regarde pour quelles valeurs de $x$ la fonction est négative et pour quelles valeurs elle est positive.
Dans les deux cas, si $a \neq 0$, la fonction $f$ s’annule en $x = \dfrac{-b}{a}$.
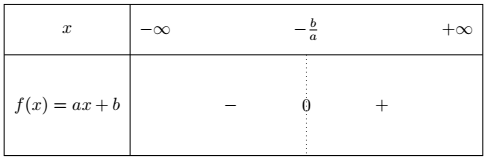
Si $a>0$, le tableau est le suivant :
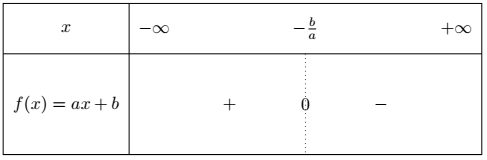
Si $a<0$, le tableau est le suivant :
Exemple
La fonction rouge est la fonction $f(x) = 0.5x + 2$. Son ordonnée à l’origine est 2.
Le coefficient directeur vaut $0.5 > 0$ donc $f$ est croissante.
La fonction $f$ s’annule pour $x = \dfrac{-2}{0.5} = -4$. Elle est négative pour $x< -4$ et positive pour $x>-4$.