Fonction inverse
Fonction inverse
Définition
Pour tout $x \in \mathbb{R}^*$, la fonction inverse est la fonction définie par $f(x) = \dfrac{1}{x}$.
On remarquera que l’ensemble de définition de la fonction inverse est $\mathbb{R}^*$ ou encore $\left]-\infty;0\right [\cup \left]0;+\infty\right[$ car on ne peut pas diviser par 0.
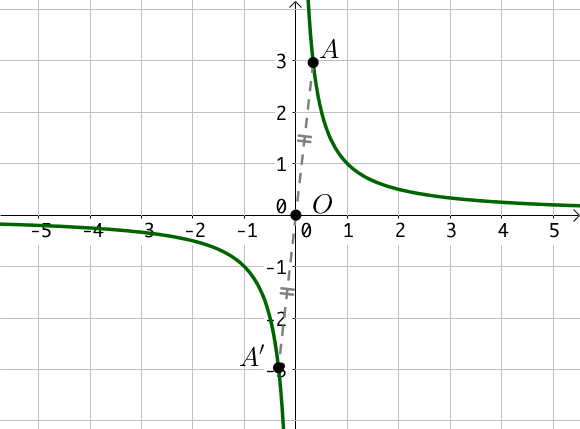
La représentation graphique de la fonction inverse est une hyperbole.
Chaque point de la courbe est le symétrique d’un autre par la symétrie centrale de centre $O(0;0)$ : la fonction inverse est une fonction impaire.
Variations
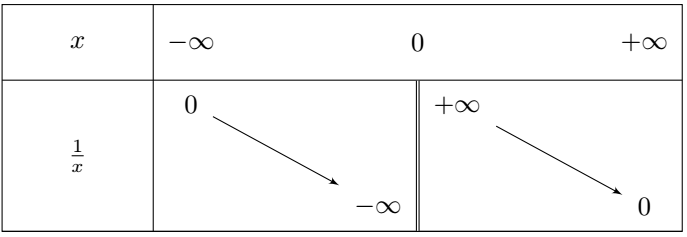
La fonction inverse est décroissante pour $x$ strictement négatif et décroissante pour $x$ strictement positif.
Son tableau de variation est le suivant :
La double barre utilisée signifie que $0$ est une valeur interdite, qui ne peut être prise.
Résolution graphique d’inéquations
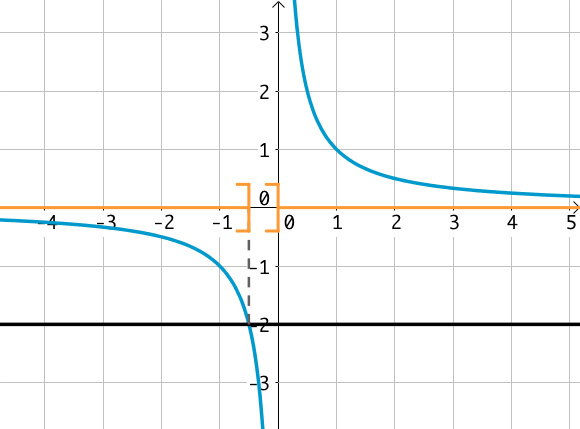
On souhaite par exemple résoudre l’inéquation $f(x) \geq -2$.
On trace pour se faire la droite d’équation $y = -2$ et les solutions sont les antécédents des points de la courbe qui sont au dessus de cette droite.
Graphiquement, les solutions sont donc $S = ]-\infty; -\dfrac{1}{2}]\ \cup \ ]0; +\infty[$ : il s’agit de la réunion de deux intervalles.
Fonction racine carrée
Fonction racine carrée
Définition
Pour tout $x \in [0; +\infty [$, la fonction racine carrée est la fonction $f(x) = \sqrt{x}$.
La racine carrée d’un nombre négatif n’existe pas.
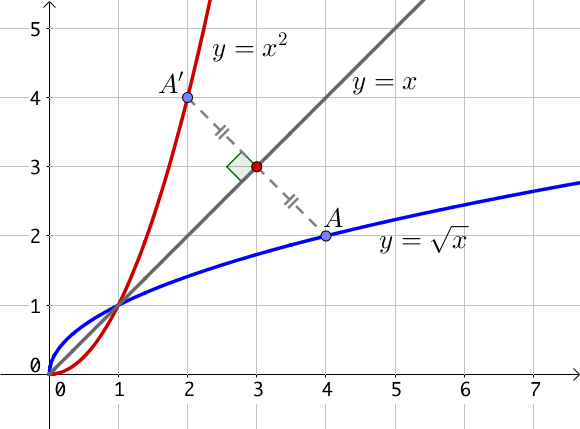
La courbe représentative de la fonction racine carrée est la symétrique par rapport à la droite $y = x$ de la fonction carré pour $x$ positif.
Variations
La fonction racine carrée est strictement croissante pour $x$ positif.
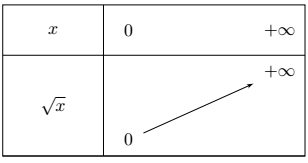
Son tableau de variation est le suivant :
Exercice d’Application
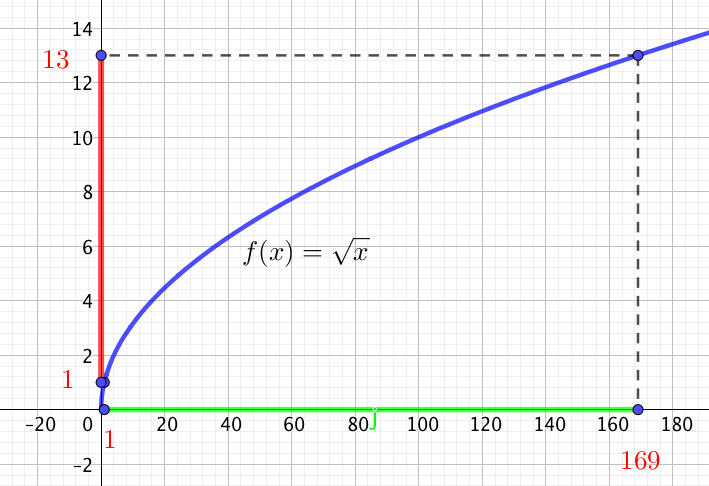
Soit $1 \leq x \leq 169$. Encadrons $\sqrt{x}$.
On sait que la fonction $f$ est croissante pour $x$ positif,
Ainsi, si $1 \leq x \leq 169$ alors $f(1) \leq f(x) \leq f(169)$ (comme $f$ est croissante, le sens des inégalités est préservé)
Ou encore $\sqrt{1} \leq \sqrt{x} \leq \sqrt{169}$
C’est à dire $1 \leq \sqrt{x} \leq 13$.
Voici une représentation graphique pour mieux comprendre :